৭. এম-তত্ত্ব : সব স্ট্রিংয়ের জননী

৭. এম-তত্ত্ব : সব স্ট্রিংয়ের জননী

যিনি মহাবিশ্বকে একটা একক দৃষ্টিভঙ্গিতে উপলব্ধি করতে পারেন তাঁর কাছে পুরো সৃষ্টি একটা অনন্য সত্য এবং প্রয়োজনীয়তা হিসেবে দৃশ্যমান হবে।

—জে. ড্যালানবেয়ার

চরম আশাবাদী মুহূর্তে আমার মনে হয়, আমরা স্ট্রিং থিওরির একেবারে শেষ পর্যায়ে পৌঁছে গেছি। তাই কল্পনা করি, যেকোনো দিন এ তত্ত্বটির চূড়ান্ত রূপ আকাশ থেকে টুপ করে ঝরে পড়বে। নির্ঘাত কারও কোলের ওপর পড়বে সেটা। কিন্তু বাস্তববাদী হিসেবে মনে হয়, আমরা এখন আগের যেকোনোটার চেয়ে আরও গভীর কোনো তত্ত্ব কাঠামোবদ্ধ করার প্রক্রিয়ায় আছি। একবিংশ শতাব্দীতেই এর অনেক গভীরে পৌঁছাতে পারব আমরা। তখন আমি এত বয়স্ক হয়ে যাব যে এ বিষয়ে আর দরকারি কোনো চিন্তাও করতে পারব না। তাই চূড়ান্ত তত্ত্বটি সত্যিই খুঁজে পাওয়া গেছে কি না, তা নিয়ে সিদ্ধান্ত নিতে হবে তরুণ পদার্থবিদদেরই।

—এডওয়ার্ড উইটেন

.

এইচ জি ওয়েলসের ১৮৯৭ সালে প্রকাশিত ক্ল্যাসিক উপন্যাস দ্য ইনভিজিবল ম্যান-এর শুরুটা হয়েছিল অদ্ভুত একটা গল্প দিয়ে। এক শীতের দিনে আচমকা অন্ধকার ফুঁড়ে একটা গ্রামে আসতে দেখা গেল এক আগন্তুককে। লোকটার গায়ে উদ্ভট আর বিচিত্র পোশাক। গোটা মুখ ঢাকা; চোখে গাঢ় নীল চশমা। মুখজুড়ে সাদা ব্যান্ডেজের কাপড়ে প্যাচানো।

শুরুতে তার প্রতি বেশ দয়াদাক্ষিণ্য দেখাল গ্রামবাসী। ভেবেছিল, লোকটা হয়তো ভয়াবহ কোনো দুর্ঘটনার কবলে পড়েছে। কিন্তু লোকটা আসার পর থেকেই গোটা গ্রামে ঘটতে শুরু করল অদ্ভুত সব কাণ্ডকারখানা। একদিন লোকটার খালি ঘরে ঢুকতেই ভয়ে চিৎকার জুড়ে দিলেন তার বাড়িওয়ালা। কারণ, তিনি দেখলেন, ঘরের ভেতর কাপড়চোপড় নিজে নিজেই শূন্যে নড়াচড়া করছে। মাথার হ্যাটটা ঘরের ভেতর একা একাই ঘুরে বেড়াচ্ছে, বিছানার চাদরটাও শূন্যে লাফিয়ে উঠছে, একা একা নড়াচড়া করছে চেয়ারটাও। ‘আসবাবপত্রগুলোও যেন পাগল হয়ে গেল’, একরাশ আতঙ্ক নিয়ে কথাগুলো বললেন তিনি।

শিগগিরই পুরো গ্রামে এসব অস্বাভাবিক ঘটনার সঙ্গে আরও কিছু গুজবের ডালপালা গজাল। অবশেষে একদল গ্রামবাসী একজোট হয়ে মুখোমুখি হলো রহস্যময় আগন্তুকের। তাদের চোখ ছানাবড়া করে দিয়ে লোকটা ধীরে ধীরে তার ব্যান্ডেজ খুলতে লাগল। জনতা বিস্ময় আর আতঙ্কে হতবুদ্ধি হয়ে গেল। ব্যান্ডেজ খোলার পর পুরোপুরি শূন্যে হারিয়ে গেল লোকটার মুখ। চোখের সামনে স্রেফ অদৃশ্য হয়ে গেল লোকটা। গ্রামবাসীর চিৎকার আর আর্তনাদের মধ্যে বিশৃঙ্খলা ছড়িয়ে পড়ল। এরপর অদৃশ্য লোকটাকে ধরতে তাড়া করে বেড়াতে লাগল তারা। কিন্তু খুব সহজেই তাদের হারিয়ে দিচ্ছিল রহস্যময় লোকটা।

বেশ কিছু ছিঁচকে অপরাধ করার পর অদৃশ্য লোকটা আগের পরিচিত এক লোককে খুঁজে বের করল। তারপর নিজের বিস্ময়কর গল্পটি বলতে শুরু করল তাকে। তার আসল নাম মি. গ্রিফেন। একটা ইউনিভার্সিটি কলেজে পড়ত লোকটা। শুরুতে চিকিৎসাশাস্ত্র শিখতে শুরু করলেও শিগগিরই এক বৈপ্লবিক পদ্ধতির দিকে ঝুঁকে পড়ে। এ পদ্ধতিতে মাংসের প্রতিফলন ও প্রতিসরণ ধর্ম বদলে ফেলা যেত। তার গুপ্ত রহস্যটি ছিল চতুর্থ মাত্রার। সে উত্তেজিতভাবে ড. কেম্পকে বলছিল, ‘একটা সাধারণ নীতির খোঁজ পাই আমি…একটা ফর্মুলা, চতুর্থ মাত্রার সঙ্গে সম্পর্কিত একটা জ্যামিতিক রাশিমালা।’

দুঃখজনক ব্যাপার হলো, এই দুর্দান্ত আবিষ্কারটা মানবকল্যাণে ব্যবহারের বদলে ডাকাতি আর ব্যক্তিগত লাভের চিন্তা ছিল তার। বন্ধুকে এই অপকর্মে আসার প্রস্তাব দেয় সে। তার দাবি অনুযায়ী, এরপর দুজন মিলে তারা বিশ্ব লুণ্ঠন করতে থাকে। কিন্তু ভয় পেয়ে পুলিশের কাছে মি. গ্রিফেনের উপস্থিতি ফাঁস করে দেয় তার বন্ধু। এ কারণে শেষ পর্যন্ত তার খোঁজে চারদিকে তল্লাশি শুরু হয়। তাতে মারাত্মকভাবে আহত হয় অদৃশ্য মানব।

সেরা বিজ্ঞান কল্পকাহিনি হিসেবে এইচ জি ওয়েলসের বেশ কিছু গল্পে বিজ্ঞানের বাজে দিকগুলো দেখানো হয়েছে। চতুর্থ স্থানিক মাত্রায় (বা বর্তমানে একে বলা হয় পঞ্চম মাত্রা। কারণ, সময় চতুর্থ মাত্রা) যিনি টোকা মারতে পারবেন, সে সত্যিই অদৃশ্য হয়ে যেতে পারবে। তখন সে এমন শক্তি অর্জন করতে পারবে, যাকে সাধারণত ভূত বা দেবতাদের শক্তি বলে বর্ণনা করা হয়। এক মুহূর্তের জন্য কল্পনা করুন, পৌরাণিক কোনো জীব একটা টেবিলের মতো দ্বিমাত্রিক জগতে বসবাস করতে পারে। যেমনটি ১৮৮৪ সালে প্রকাশিত এডউইন অ্যাবটের ফ্ল্যাটল্যান্ড-এ দেখা যায়। তাদের চারপাশে যে একটা তৃতীয় মাত্রার মহাবিশ্ব আছে, সে কথা ঘুণাক্ষরেও না জেনে নিজেদের কর্মকাণ্ড চালিয়ে যায় তারা।

কিন্তু ফ্ল্যাটল্যান্ড বা সমতল বিশ্বের কোনো বিজ্ঞানী যদি এমন কোনো পরীক্ষা চালান, যা দিয়ে তিনি টেবিলে ইঞ্চিখানেক বাইরে ঘোরাফেরা করার সুযোগ পাবেন, তাহলে অদৃশ্য হয়ে যেতে পারবেন তিনি। কারণ, আলো তার নিচ দিয়ে এমনভাবে অতিক্রম করবে যেন সেখানে তার কোনো অস্তিত্ব‍ই নেই। সমতল বিশ্বের সামান্য একটু ওপরে ভেসে, তিনি তার নিচে থাকা টেবিলের ওপরের ঘটনাগুলো ঘটতে দেখতে পারতেন। হাইপারস্পেসে ভেসে থাকলে নিঃসন্দেহে কিছু সুবিধা পাওয়া যাবে। হাইপারস্পেস থেকে কেউ যদি নিচে তাকায়, তাহলে দেবতাদের মতো শক্তিও অর্জন করতে পারবে সে।

তার নিচ দিয়ে আলো অতিক্রম করার কারণে তাকে অদৃশ্য করে তুলবে। শুধু তা-ই নয়, বস্তুর ভেতর দিয়েও সে চলে যেতে পারবে অনায়াসে। অন্য কথায়, সে ইচ্ছেমতো অদৃশ্য হয়ে যেতে পারবে। এমনকি হেঁটে চলে যেতেও পারবে দেয়ালের ভেতর দিয়ে। শুধু এক লাফে তৃতীয় মাত্রায় চলে যাওয়ার কারণে সে সমতল মহাবিশ্ব থেকে স্রেফ উধাও হয়ে যাবে। এরপর লোকটা যদি টেবিলের ওপর লাফ দিয়ে ফিরে আসে, তাহলে হুট করে শূন্য থেকে সেখানে উদয় হয়েছে বলে মনে হবে। তাই যেকোনো জেলখানা থেকে পালিয়ে যেতে পারবে। ফ্ল্যাটল্যান্ডের জেলখানাও হবে কয়েদির চারপাশে আঁকা বৃত্ত দিয়ে গঠিত। কাজেই সেখান থেকে খুব সহজে লাফ দিয়ে তৃতীয় মাত্রায় ও তার বাইরে চলে যাওয়া যাবে।

হাইপারস্পেসে থাকা কোনো জীবের কাছ থেকে কিছু গোপন রাখা অসম্ভব হয়ে পড়বে। কোনো ভল্টে আটকানো সোনাদানা খুব সহজে দেখা যাবে তৃতীয় মাত্রার সুবিধাজনক জায়গা থেকে। কারণ, তার কাছে ভল্ট খোলা পড়ে থাকবে আয়তক্ষেত্রের মতো। ওই আয়তক্ষেত্রের মধ্যে পৌঁছানো তার জন্য ছেলেখেলা ব্যাপার। আবার ভল্টটি না ভেঙেই সেখান থেকে সোনাদানা তুলে নিতে পারবে সে। আবার চামড়া না কেটেই সার্জারি করাও সম্ভব হবে।

ঠিক এভাবে চতুর্থ মাত্রিক বিশ্বের ধারণা তুলে ধরতে চেয়েছিলেন এইচ জি ওয়েলসও। সেখানে চতুর্থমাত্রিক বিশ্বের কাছে আমরা হলাম ফ্ল্যাটল্যান্ডার। আমাদের ঠিক ওপরে ওই উচ্চতর তলের অস্তিত্ব হয়তো আছে। আমরা বিশ্বাস করি, আমাদের বিশ্বে আমরা যা দেখি, ঠিক তা-ই আছে। আমাদের নাকের ডগায় যে গোটা একটা মহাবিশ্ব ঝুলে থাকতে পারে, সে সম্পর্কে আমরা সচেতন নই। অবশ্য আমাদের কয়েক ইঞ্চি ওপরে হয়তো চতুর্থ মাত্রা ভাসমান আরেকটি মহাবিশ্ব ঝুলে আছে। কিন্তু এ মহাবিশ্বকে আমাদের কাছে মনে হবে অদৃশ্য।

উচ্চমাত্রার কোনো জীব অতিমানবিক ক্ষমতা অর্জন করে। তাই স্বভাবতই তাকে বর্ণনা করা হবে ভূত বা আত্মা হিসেবে। আরেকটা বিজ্ঞান কল্পকাহিনিতে এইচ জি ওয়েলস প্রশ্ন তোলেন, অতিপ্রাকৃতিক জীবন হয়তো উচ্চমাত্রায় বাস করে। সেখানে তিনি এমন এক প্রশ্ন তোলেন যে তা এখন ব্যাপক জল্পনাকল্পনা আর গবেষণার বিষয় হয়ে দাঁড়িয়েছে। তাঁর প্রশ্নটা ছিল : এসব উচ্চমাত্রায় কি পদার্থবিজ্ঞানের সূত্র নতুন বা অন্য কিছু হবে? ১৮৯৫ সালে লেখা দ্য ওয়ান্ডারফুল ভিজিট উপন্যাসে দুর্ঘটনাক্রমে এক দেবদূতকে গুলি করে বসেন গির্জার এক যাজক। আমাদের মাত্রার ভেতর দিয়ে যাচ্ছিলেন ওই দেবদূত। কিছু মহাজাগতিক কারণে আমাদের মাত্রা এবং এক সমান্তরাল মহাবিশ্ব সাময়িক সংঘর্ষের মুখে পড়ে। তাতে আমাদের বিশ্বের মধ্যে পড়ে যান দেবদূত। এ গল্পে ওয়েলস লিখেছেন, ‘এখানে যেকোনোসংখ্যক তিন মাত্রিক মহাবিশ্ব একটার সঙ্গে আরেকটা গাদাগাদি হয়ে থাকতে পারে। যাজক আহত দেবদূতকে প্রশ্ন করেন। জবাব পেয়ে যাজক বিস্ময়ের সঙ্গে বুঝতে পারেন, আমাদের প্রকৃতির সূত্র দেবদূতদের বিশ্বে প্রয়োগ করা যায় না। যেমন তাদের মহাবিশ্বে কোনো তল সিলিন্ডারাকৃতির। কাজেই সেখানে স্থান নিজেই বক্র। (আইনস্টাইন সাধারণ আপেক্ষিকতা আবিষ্কারের ২০ বছর আগে বক্র পৃষ্ঠতলের ওপর টিকে থাকা মহাবিশ্ব সম্পর্কে ওয়েলসের এ ভাবনাটি ছিল অভিনব।) একে ওই যাজক বর্ণনা করেছেন এভাবে, ‘তাদের জ্যামিতি আলাদা, কারণ তাদের স্থান বক্র। তাই সব তল সেখানে সিলিন্ডার আকৃতির। তাদের মহাকর্ষ সূত্রও আমাদের বিপরীত বর্গীয় সূত্রের মতো নয়। আবার তাদের মৌলিক রং মাত্র তিনটি নয়, ২৪টি।’ ওয়েলস গল্পটি লেখার এক শতাব্দীর বেশি কাল পরে পদার্থবিদেরা এখন বুঝতে পারছেন, সমান্তরাল মহাবিশ্বে হয়তো নতুন কোনো ভৌত সূত্র থাকতে পারে। সেখানে সম্ভবত থাকতে পারে ভিন্ন ধরনের অতিপারমাণবিক কণা, পরমাণু আর রাসায়নিক বিক্রিয়া। (নবম অধ্যায়ে আমরা দেখব, আমাদের ঠিক ওপরে সমান্তরাল মহাবিশ্বগুলো থাকার সম্ভাবনা রয়েছে। সেগুলো শনাক্ত করতে এখন বেশ কিছু পরীক্ষা-নিরীক্ষা চলছে। )

হাইপারস্পেস বা উচ্চতর স্থানের ধারণায় আগ্রহী হয়েছেন চিত্রশিল্পী, সংগীতশিল্পী, অধ্যাত্মবাদী, ধর্মতাত্ত্বিক ও দার্শনিকেরা। বিশেষ করে বিশ শতকের শুরুর দিকে এ ঘটনা ঘটতে দেখা যায়। আর্টবিষয়ক ইতিহাসবিদ লিন্ডা ডালরিম্পল হেন্ডারসনের মতে, চতুর্থ মাত্রায় প্রভাবিত হয়ে কিউবিজম সৃষ্টি করেছিলেন পাবলো পিকাসো। (তাঁর আঁকা নারীদের চোখ সরাসরি আমাদের দিকে হলেও নাক অন্য পাশে। ফলে ওই নারীদের আমরা সম্পূর্ণভাবে দেখতে পাই। একইভাবে উচ্চতর স্থানের কোনো জীব নিচের দিকে তাকালে আমাদের গোটাটাই একসঙ্গে দেখতে পাবে : সামনে, পেছনে ও পার্শ্বগুলো একই সঙ্গে।) সালভাদর দালির বিখ্যাত চিত্র ক্রিস্টাস হাইপারকিউবাস-এ তিনি ক্রুশবিদ্ধ যিশুকে এঁকেছেন একটা চুপসে যাওয়া চারমাত্রিক হাইবারকিউব বা টেসারেক্টের সামনে। দ্য পারসিসটেন্স অব মেমোরিছবিতে চতুর্থ মাত্রার সঙ্গে ঘড়িগুলো গলে যাওয়ার দৃশ্য দিয়ে সময়ের ধারণা তুলে ধরার চেষ্টা করেছেন দালি। মার্সেল ডুশাম্পের ন্যুড ডিসেন্ডিং আ স্টেয়ারকেস (নং ২) ছবিতে আমরা এক নগ্নিকাকে থমকে যাওয়া কালের ধীরগতি সিঁড়ি দিয়ে নিচে নেমে যেতে দেখি। এখানেও দ্বিমাত্রিক তলে সময়ের চতুর্থ মাত্রাকে ধরার চেষ্টা করা হয়েছে।

এম-তত্ত্ব

বর্তমানে চতুর্থ মাত্রার চারপাশের রহস্য আর কিংবদন্তি নতুন করে পুনরুজ্জীবিত হচ্ছে সম্পূর্ণ ভিন্ন এক কারণে। এর পেছনের কারণ স্ট্রিং থিওরি আর তার সর্বশেষ প্রতিমূর্তি এম-থিওরি। ঐতিহাসিকভাবে হাইপারস্পেসের ধারণা ঠেকিয়ে রাখতে ব্যাপক চেষ্টা করেছেন পদার্থবিদেরা। একসময় উচ্চতর মাত্রাকে তাচ্ছিল্য করতে তাঁরা বলতেন যে ওটা অধ্যাত্মবাদ আর জালিয়াতের রাজ্য। যে বা যারা গুরুত্বের সঙ্গে অদৃশ্য জগতের অস্তিত্বের প্রস্তাব করত, তারা ব্যঙ্গ-বিদ্রূপের শিকার হতো বিজ্ঞানীদের কাছে।

কিন্তু সবকিছু বদলে গেল এম-থিওরি আসার পর। উচ্চতর মাত্রা এখন পদার্থবিদ্যার গভীর এক বিপ্লবের কেন্দ্রবিন্দু। কারণ সবচেয়ে বড় সমস্যাটির সঙ্গে লড়াই করতে এখন বাধ্য হচ্ছেন পদার্থবিদেরা। আর সে সমস্যাটা হলো সাধারণ আপেক্ষিকতা আর কোয়ান্টাম তত্ত্বের মধ্যকার ফাটল। লক্ষণীয় ব্যাপার হলো, এই তত্ত্ব দুটিকে একেবারে মৌলিক পর্যায়ে মহাবিশ্বসম্পর্কিত সব ভৌত জ্ঞানের সমষ্টি বলা যায়। বর্তমানে একমাত্র এম-থিওরিই এই দুটি বড় তত্ত্বকে একীভূত করার ক্ষমতা রাখে। মহাবিশ্বের পরস্পরবিরোধী তত্ত্ব বলে মনে হওয়া এই তত্ত্ব দুটিকে একটা সংগতিপূর্ণ সমষ্টি আকারে একীভূত করে একটা থিওরি অব এভরিথিং’ বা ‘সার্বিক তত্ত্ব’ প্রণয়ন করতে পারে এম-তত্ত্ব। গত শতাব্দীতে এ ধরনের অনেকগুলো তত্ত্বের প্রস্তাব করা হয়েছে। কিন্তু তাদের মধ্যে একমাত্র সম্ভাব্য যে তত্ত্বটি আইনস্টাইনের ভাষায় ‘ঈশ্বরের মন পড়তে পারে’ সেটি হলো এম-তত্ত্ব।

প্রকৃতির সব বলকে একীভূত করে একটা অভিজাত তত্ত্ব প্রণয়ন করতে শুধু দশ বা এগারোমাত্রিক হাইপারস্পেসের পরিসর পর্যাপ্ত। অবিশ্বাস্য রকমের এই তত্ত্ব চিরন্তন প্রশ্নগুলোর উত্তরও দিতে পারে : সবকিছু শুরুর আগে কী ঘটেছিল? সময় কি উল্টো দিকে যেতে পারে? মাত্রাগত প্রবেশপথের ভেতর দিয়ে আমরা কি এই মহাবিশ্বের অন্য কোনো প্রান্তে নিয়ে যেতে পারি? (অবশ্য এই তত্ত্বের সমালোচকেরা বলেন, আমাদের বর্তমানের পরীক্ষামূলক দক্ষতায় এই তত্ত্বকে পরীক্ষা করে দেখা অসম্ভব। তাদের ইঙ্গিতটা আসলে সঠিক। অবশ্য তত্ত্বটি পরীক্ষা করার জন্য বর্তমানে অনেকগুলো পরিকল্পনা করা হচ্ছে। সেগুলো হয়তো এই পরিস্থিতি একসময় বদলেও দিতে পারে। এ বিষয়ে আমরা বিস্তারিত আলোচনা করব নবম অধ্যায়ে।)

মহাবিশ্বের একটা সত্যিকার একীভূত ব্যাখ্যা প্রণয়নে গত পঞ্চাশ বছরের সব চেষ্টা লজ্জাজনক ব্যর্থতার মধ্য দিয়ে শেষ হয়েছে। ধারণাগতভাবে সেটা বোঝা বেশ সহজ। সাধারণ আপেক্ষিকতা ও কোয়ান্টাম তত্ত্ব প্রায় সব ক্ষেত্রেই চরম বিপরীত স্বভাবের। সাধারণ আপেক্ষিকতা বড় পরিসরের একটা তত্ত্ব। এটি কৃষ্ণগহ্বর, মহাবিস্ফোরণ, কোয়াসার ও প্রসারণশীল মহাবিশ্বের ব্যাখ্যা করে। বিছানার চাদর আর ট্রাম্পোলিনে জালের মতো মৃসণ তলের গণিতের ওপর ভিত্তি করে গড়ে উঠেছে তত্ত্বটি। অন্যদিকে কোয়ান্টাম তত্ত্ব একেবারে উল্টো। এটা খুব ক্ষুদ্র জগৎ ব্যাখ্যা করে। যেমন পরমাণু, প্রোটন, নিউট্রন ও কোয়ার্ক। এটি কোয়ান্টা নামের একটা বিচ্ছিন্ন শক্তির প্যাকেটের তত্ত্বের ওপর ভিত্তি করে গড়ে উঠেছে। আপেক্ষিকতার বিপরীতে গিয়ে, কোয়ান্টাম তত্ত্ব বলে, শুধু ঘটনার সম্ভাবনা নির্ণয় করা যায়। কাজেই আমরা কখনো কোনো ইলেকট্রনের সঠিক অবস্থান জানতে পারব না। এ তত্ত্ব দুটি গড়ে উঠছে ভিন্ন ধরনের দুই গণিতকে ভিত্তি করে। কাজেই তাদের যে একীভূত করার সব চেষ্টা বিফল হবে, তাতে অবাক হওয়ার কিছু নেই।

আইনস্টাইনকে অনুসরণ করে নিজের হাতে একটা ইউনিফায়েড ফিল্ড থিওরি বা একীভূত ক্ষেত্র তত্ত্ব প্রণয়নের চেষ্টা করেছেন আরউইন শ্রোডিঙ্গার, ওয়ার্নার হাইজেনবার্গ, উলফগ্যাং পাউলি এবং আর্থার এডিংটনের মতো পদার্থবিজ্ঞান জগতের জায়ান্টরা। কিন্তু সবগুলো দুঃখজনক ব্যর্থতার শিকার হয়েছে। ১৯২৮ সালে আইনস্টাইনের ইউনিফায়েড ফিল্ড থিওরির প্রাথমিক সংস্করণ নিয়ে আকস্মিকভাবে গণমাধ্যমের মধ্যে প্রতিযোগিতার সৃষ্টি হয়। এমনকি নিউইয়র্ক টাইমস-এ একটা সমীকরণসহ ওই প্রবন্ধের অংশবিশেষও ছাপা হয়েছিল। শিগগিরই তার বাড়ির বাইরে ঝাঁক বেঁধে অবস্থান নিতে শুরু করেন শতাধিক রিপোর্টার। ইংল্যান্ড থেকে আইনস্টাইনের কাছে এডিংটন লিখলেন, ‘তুমি হয়তো শুনে মজা পাবে, লন্ডনে আমাদের অন্যতম বড় ডিপার্টমেন্ট স্টোর তাদের জানালায় তোমার পেপারটা আঠা দিয়ে লাগিয়ে দিয়েছে (ছয়টি পাতা একটার পর একটা সারিবদ্ধভাবে), যাতে পথচারীরা সবাই তা পড়তে পারে। ওটা পড়ার জন্য তার চারপাশে বড় ধরনের ভিড় হচ্ছে।’

এর কয়েক বছর পর একীভূত তত্ত্বের ভূতের আসর পড়ে আরউইন শ্রোডিঙ্গারের ওপর। ১৯৪৬ সালে তিনিও একটা কিছু আবিষ্কার করে বসেন। সেটাকেই বহুল আলোচিত ইউনিফায়েড ফিল্ড থিওরি বলে মনে হয়েছিল তাঁর নিজের কাছে। তড়িঘড়ি করে এমন এক কাজ করে বসেন, যাকে সেকালের জন্য কিছুটা অস্বাভাবিক বলা যায় (অবশ্য এখন একে আর অস্বাভাবিক বলার উপায় নেই)। একটা প্রেস কনফারেন্স ডাকেন শ্রোডিঙ্গার। এমনকি শ্রোডিঙ্গারের কথা শুনতে ওই সংবাদ সম্মেলনে উপস্থিত থাকতে দেখা গেছে আয়ারল্যান্ডের প্রধানমন্ত্রী ইমোন ডি ভ্যালেরাকেও। তাঁকে যখন জিজ্ঞেস করা হলো, শেষ পর্যন্ত যে তিনি একটা ইউনিফায়েড ফিল্ড থিওরি আবিষ্কার করতে পেরেছেন, সে ব্যাপারে তিনি কতটা নিশ্চিত। উত্তরে শ্রোডিঙ্গার বললেন, ‘আমার বিশ্বাস, আমি সঠিক। যদি ভুল করে থাকি, তাহলে আমাকে চরম বোকাটে দেখাবে।’ (এই সংবাদ সম্মেলনের খোঁজ পেয়ে নিউইয়র্ক টাইমস একসময় পাণ্ডুলিপি জোগাড় করে তা আইনস্টাইন ও অন্যদের কাছে পাঠায় মন্তব্য করার জন্য। দুঃখজনক ব্যাপার হলো, আইনস্টাইন বুঝতে পারলেন, আসলে পুরোনো একটা তত্ত্ব নতুন করে আবিষ্কার করে বসেছেন শ্রোডিঙ্গার। সেই তত্ত্ব তিনি নিজেই অনেক আগে প্রস্তাব করেছিলেন। সেটা তখন নাকচও হয়ে গিয়েছিল। বেশ ভদ্রভাবে প্রতিক্রিয়া জানালেন আইনস্টাইন। তবু এতে বেশ অপমানিত হন শ্রোডিঙ্গার। )

১৯৫৮ সালে কলাম্বিয়া বিশ্ববিদ্যালয়ে এক বক্তৃতায় অংশ নেন পদার্থবিদ জেরেমি বার্নস্টেইন। সেখানে নিজের আবিষ্কৃত ইউনিফায়েড ফিল্ড থিওরি সবার সামনে পেশ করেন উলফগ্যাং পাউলি। এটা তিনি গড়ে তুলেছিলেন ওয়ার্নার হাইজেনবার্গকে সঙ্গে নিয়ে। সেদিন দর্শকসারিতে উপস্থিত ছিলেন নীলস বোর। কিন্তু তিনি মুগ্ধ হতে পারেননি। শেষ পর্যন্ত বোর ঝট করে দাঁড়িয়ে বললেন, ‘আমরা যারা পেছনে বসে আছি, তারা বুঝতে পারছি, তোমার তত্ত্বটা উদ্ভট। কিন্তু তত্ত্বটা যথেষ্ট উদ্ভট কি না, তা নিয়ে আমরা দ্বিধাবিভক্ত।’

বোর কী বলতে চাচ্ছেন, তা বুঝতে আর বাকি রইল না পাউলির। সেটা হলো, হাইজেনবার্গ আর পাউলির তত্ত্বটা এতই প্রচলিত আর সাধারণ মানের যে সেটা কোনোভাবেই ইউনিফায়েড ফিল্ড থিওরি হতে পারে না। ‘ঈশ্বরের মন পড়ার’ মানে হলো, আমূল পাল্টে দেওয়ার মতো ভিন্ন ধরনের গণিত আর আইডিয়ার প্রবর্তনের দরকার।

অনেক পদার্থবিদ বিশ্বাস করেন, সবকিছুর পেছনে সরল, মার্জিত এবং অনস্বীকার্য কোনো তত্ত্ব আছে, যেটা খ্যাপাটে ও উদ্ভট হলেও সত্য। প্রিন্সটনের জন হুইলার উল্লেখ করেন, উনিশ শতকে পৃথিবীতে দেখতে পাওয়া জীবনের বিপুল বৈচিত্র্যের ব্যাখ্যা করা অর্থহীন মনে হয়েছিল। কিন্তু চার্লস ডারউইন প্রাকৃতিক নির্বাচন তত্ত্ব চালু করেন। এই একটিমাত্র তত্ত্বই পৃথিবীর সব জীবের উৎপত্তি ও বৈচিত্র্যের ব্যাখ্যা জোগান দিতে পেরেছিল।

নোবেল বিজয়ী পদার্থবিদ স্টিভেন ওয়াইনবার্গ এ ক্ষেত্রে ভিন্ন একটা উপমা ব্যবহার করেন। কলম্বাসের পর, ইউরোপের প্রথম দিককার অনুসন্ধানকারীরা মানচিত্রগুলোর খুঁটিনাটি বিষয় ব্যবহার করতে শুরু করে। একসময় তাঁরা জোরালোভাবে ইঙ্গিত করেন, উত্তর মেরুর অস্তিত্ব অবশ্যই আছে। কিন্তু এ বিষয়ে কোনো প্রত্যক্ষ প্রমাণ ছিল না তাঁদের কাছে। পৃথিবীর প্রতিটি মানচিত্রে বিশাল একটা ফাঁকা স্থান দেখায়, সেখানে উত্তর মেরু থাকা উচিত। সে কারণে প্রথম দিককার অনুসন্ধানকারীরা সরলভাবে অনুমান করলেন, একটা উত্তর মেরু থাকা উচিত। কিন্তু কেউই সেটা কখনো দেখতে পায়নি। একইভাবে আগের সেই অনুসন্ধানকারীদের মতো একটা থিওরি অব এভরিথিং থাকার পরোক্ষ প্রমাণ পাচ্ছেন বর্তমানের পদার্থবিদেরাও। কিন্তু সে তত্ত্বটা আসলে কী, তা নিয়ে এখনো কোনো সর্বজনীন ঐকমত্য নেই।

স্ট্রিং তত্ত্বের ইতিহাস

ইউনিফায়েড ফিল্ড থিওরি হওয়ার মতো ‘যথেষ্ট উদ্ভট’ একটা তত্ত্ব হলো স্ট্রিং থিওরি বা এম-থিওরি। পদার্থবিদ্যার জগতে সম্ভবত স্ট্রিং থিওরির ইতিহাসই সবচেয়ে বিচিত্র। এ তত্ত্ব আবিষ্কৃত হয়েছিল অনেকটা দুর্ঘটনাক্রমে। ভুল একটা সমস্যায় প্রয়োগ করা হয়েছিল একে। ফলে গুরুত্ব হারিয়ে তা আড়ালে চাপা পড়ে। তারপর একদিন সেটা একটা থিওরি অব এভরিথিং হিসেবে পুনর্জন্ম লাভ করে হুট করে। চূড়ান্ত বিশ্লেষণে এ তত্ত্বটিকে ধ্বংস করা ছাড়া ছোটখাটো সামঞ্জস্যে আনা অসম্ভব। তাই তত্ত্বটা হয় একটা ‘থিওরি অব এভরিথিং’, নয়তো ‘থিওরি অব নাথিং’।

এই অদ্ভুত ইতিহাসের কারণ হলো স্ট্রিং থিওরি এক অর্থে বিকশিত হয়েছে পেছনের দিকে। সাধারণত আপেক্ষিকতার মতো কোনো তত্ত্বের শুরু হয় মৌলিক ভৌত নীতির মাধ্যমে। এরপর এসব নীতিতে শাণ দিয়ে মৌলিক চিরায়ত সমীকরণ গুচ্ছ পাওয়া যায়। সবশেষে এসব সমীকরণের কোয়ান্টাম ফ্ল্যাকচুয়েশন নির্ণয় করেন কেউ একজন। কিন্তু স্ট্রিং থিওরি বিকশিত হয়েছে পেছন দিকে। অর্থাৎ এর শুরু হয়েছিল কোয়ান্টাম তত্ত্বের একটা আকস্মিক আবিষ্কারের মাধ্যমে। এই তত্ত্বের ভৌত নীতি কোন দিকে নিয়ে যেতে পারে, তা নিয়ে এখনো বেশ ধাঁধায় মধ্যে পড়ে যান পদার্থবিদেরা।

স্ট্রিং থিওরির উৎপত্তি সেই ১৯৬৮ সালে। সেবার জেনেভার সার্নের নিউক্লিয়ার ল্যাবরেটরিতে গ্যাবরিয়েল ভেনেজিয়ানো এবং মাহিকো সুজুকি নামের দুজন পদার্থবিদ আলাদাভাবে একটা গণিত বইয়ের পাতা ওলটাচ্ছিলেন। হঠাৎ বইয়ের পাতায় অয়েলারের বেটা ফাংশনের ওপর হুমড়ি খেয়ে পড়েন তাঁরা। ধোঁয়াশায় ভরা এই গাণিতিক রাশিমালাটি আঠারো শতকে আবিষ্কার করেছিলেন গণিতবিদ লিয়নার্দো অয়েলার। বেটা ফাংশন অদ্ভুতভাবে অতিপারমাণবিক জগৎকে ব্যাখ্যা করতে পারে বলে মনে হয়েছিল। বিস্ময়ে তাঁরা দেখেন, এ বিমূর্ত গাণিতিক সূত্রটি দুটি পাই মেসন কণার বিপুল শক্তির সংঘর্ষ ব্যাখ্যা করতে পারে। শিগগির পদার্থবিজ্ঞানে এক হইচই ফেলে দিল ভেনেজিয়ানো মডেল। নিউক্লিয়ার বলের ব্যাখ্যার সাধারণীকরণের প্রচেষ্টায় আক্ষরিক অর্থেই লেখা হয়ে গেল শ খানেক পেপার।

সহজ কথায়, তত্ত্বটি আবিষ্কৃত হলো সত্যিই এ রকম আকস্মিকভাবে। ইনস্টিটিউট অব অ্যাডভান্সড স্টাডির এডওয়ার্ড উইটেন বলেছেন, ‘অধিকারবলে বিশ শতকের পদার্থবিদদের এই তত্ত্বে গবেষণা করার সুযোগ না পেলেই ভালো হতো। অধিকার বলে, স্ট্রিং থিওরি আবিষ্কৃত হওয়া উচিত হয়নি।’ (অনেকের বিশ্বাস, এই তত্ত্বের বেশ কিছু চমকপ্রদ বড় সাফল্যের পেছনে সৃষ্টিশীল চালকের ভূমিকা পালন করেছেন এডওয়ার্ড উইটেন।

সে সময় স্ট্রিং থিওরি যে চাঞ্চল্য সৃষ্টি করেছিল, সে স্মৃতি আমার কাছে এখনো জীবন্ত। আমি তখনো যুক্তরাষ্ট্রের বার্কলিতে ক্যালিফোর্নিয়া বিশ্ববিদ্যালয়ের গ্র্যাজুয়েট শিক্ষার্থী। পদার্থবিদেরা তাঁদের মাথা নেড়ে বিবৃতি দিচ্ছিলেন, পদার্থবিজ্ঞান এভাবে হওয়া উচিত নয়। সেসব দৃশ্য এখনো আমার চোখে ভাসে। অতীতে পদার্থবিদ্যা গড়ে ওঠার সাধারণ ভিত্তি ছিল : অনেক কষ্ট সয়ে প্রকৃতিকে বিশদভাবে পর্যবেক্ষণ করা, কিছু আংশিক হাইপোথিসিস সূত্রবদ্ধ করা, ওই আইডিয়াকে অতি সাবধানে উপাত্তের সঙ্গে পরীক্ষা করে দেখা এবং তারপর বিরক্তিকরভাবে বারবার একই পদ্ধতি পুনরায় অনুসরণ করা। কিন্তু স্ট্রিং থিওরির পদ্ধতিটা অনেকটা পকেট থেকে জাদুমন্ত্রের মতো বেরিয়ে আসা আবিষ্কারের মতো। কারণ, তত্ত্বটি আবিষ্কৃত হয়েছে সরলভাবে উত্তর অনুমান করে। এ রকম রোমাঞ্চকর শর্টকাট সম্ভবত আগে কখনো সম্ভব হতে দেখা যায়নি।

আমাদের সবচেয়ে শক্তিশালী যন্ত্রপাতি ব্যবহার করেও অতিপারমাণবিক কণাদের দেখা যায় না। সে কারণে তাদের বিশ্লেষণ করতে একটা নিষ্ঠুর, কিন্তু বেশ কার্যকর এক পদ্ধতি উদ্ভাবন করেছেন পদার্থবিদেরা। পদ্ধতিটা হলো এসব কণাকে বিপুল শক্তিতে একসঙ্গে সংঘর্ষ ঘটিয়ে চূর্ণ-বিচূর্ণ করা। অনেক মাইল এলাকাজুড়ে বিস্তৃত বিশাল আকৃতির একটা অ্যাটম স্ম্যাশার বা পরমাণু চূর্ণকারক কিংবা পার্টিকেল অ্যাকসিলারেটর বানাতে খরচ করা হয়েছে কয়েক বিলিয়ন ডলার। এতে অতিপারমাণবিক কণাদের বিম তৈরি করে সেগুলোকে পরস্পরের সঙ্গে সংঘর্ষ ঘটানো হয়। এরপর এ সংঘর্ষ থেকে পাওয়া ভগ্নাংশের খুঁটিনাটি অতি যত্নের সঙ্গে বিশ্লেষণ করেন পদার্থবিদেরা। এ কষ্টকর ও দুঃসাধ্য প্রক্রিয়ার উদ্দেশ্য হলো, একটা ধারাবাহিক সংখ্যা তৈরি করা, যাকে বলা হয় স্ক্যাটারিং ম্যাটিকস বা এস-ম্যাট্রিকস। এসব সংখ্যা গুরুত্বপূর্ণ হওয়ার কারণ হলো, এর মধ্যে অতিপারমাণবিক পদার্থবিদ্যার সব তথ্য লিপিবদ্ধ থাকে। অর্থাৎ এস-ম্যাট্রিকস জানা গেলে মৌলিক কণার সব ধর্ম সম্পর্কে সিদ্ধান্ত নেওয়া যায়।

মৌলিক কণা পদার্থবিজ্ঞানের অন্যতম লক্ষ্য হলো, সবল মিথস্ক্রিয়ার জন্য এস-ম্যাট্রিকসের গাণিতিক কাঠামোর অনুমান করা। এই লক্ষ্যটি এত কঠিন যে অনেক পদার্থবিদের বিশ্বাস, এটা জানা পদার্থবিজ্ঞানের বাইরের কোনো ব্যাপার। এটা বুঝতে পারলেই কল্পনা করা যাবে যে কেন ভেনেজিয়ানো এবং সুজুকির কারণে চাঞ্চল্যের সৃষ্টি হয়েছিল। একটা গণিতের বইয়ের পাতা উল্টে তখন সরলভাবে এস-ম্যাট্রিকস অনুমান করেন এই দুই বিজ্ঞানী।

এই মডেলটা একেবারেই ভিন্ন ধরনের জীবের মতো, যা আগে কখনো দেখা যায়নি। সাধারণত কেউ যখন নতুন তত্ত্ব প্রণয়ন করে (ধরা যাক কোয়ার্ক), পদার্থবিদেরা তখন ওই তত্ত্বকে আনাড়ির মতো মেরামতের চেষ্টা করেন, পরিবর্তন আনেন সরল প্যারামিটারগুলোতে (কণার ভর বা কাপলিং শক্তির মতো বিষয়গুলো)। কিন্তু ভেনেজিয়ানোর মডেলের কাঠামো ছিল খুবই নিখুঁত। তাই দেখা গেল, তার মৌলিক প্রতিসাম্যতায় সামান্যতম গোলমালেও গোটা সূত্রটা ধসে পড়ে। মার্জিত কাঠামোর কোনো ক্রিস্টালের টুকরোর মতো যেন সেটা, যার আকৃতিতে কোনো পরিবর্তনের চেষ্টা করা হলেও তা যেন ভেঙে চুরমার হয়ে যায়।

ওই যে শ খানেক পেপারের কথা বললাম, সেগুলোতে প্যারামিটারগুলোর অতিসামান্য বদল আনা হয়েছিল। তাতে নষ্ট হয়ে গেল এ মডেলের স্বকীয় সৌন্দর্য। সেগুলোর একটাও এখন আর টিকে নেই। এর মধ্যে কেবল একটা পেপারকে এখনো স্মরণ করা হয়। এ পেপারটাতে বোঝার চেষ্টা করা হয়েছিল যে এই তত্ত্বটা কাজ করে কেন। অর্থাৎ যে পেপারটা এই মডেলের সিমেট্রি বা প্রতিসাম্যতা উন্মোচনের চেষ্টা করেছিল। ধীরে ধীরে পদার্থবিদেরা বুঝতে পারলেন, এই তত্ত্বের কোনো মানানসই প্যারামিটার নেই।

ভেনেজিয়ানো মডেল যতটা আকর্ষণীয়, তার সমস্যাও ছিল ঠিক ততটাই। প্রথমত পদার্থবিদেরা বুঝতে পারলেন, এটা আসলে চূড়ান্ত এস-ম্যাট্রিকসের প্রথম একটা আসন্নতা। আবার তা পুরো চিত্রও তুলে ধরে না। এরপর উইসকনসিন বিশ্ববিদ্যালয়ের বানজি সাকিতা, মিগুয়েল ভিরাসোরো এবং কেইজি কিক্কায়া উপলব্ধি করলেন, এই এস-ম্যাট্রিকসকে একটা অসীম ধারা হিসেবে দেখা যায়। ফলে ভেনেজিয়ানো মডেল হয়ে উঠল ওই ধারায় প্রথম ও গুরুত্বপূর্ণ পদ। (মোটা দাগে বললে, ওই সিরিজের প্রতিটি পদ সেই সংখ্যার প্রতীক, যাতে কণাগুলো পরস্পরের সঙ্গে ধাক্কা খেতে পারে। এই বিজ্ঞানীরা কিছু নিয়ম অনুমান করলেন, যেগুলো দিয়ে তাঁদের আসন্নতায় উচ্চতর পদ বানানো যায়। নিজের পিএইচডি থিসিসে, এই প্রোগ্রামটি সম্পূর্ণ করার ও ভেনেজিয়ানো মডেলের সম্ভাব্য সব সংশোধনী করার সিদ্ধান্ত নিই আমি। আমার সহকর্মী এল পি ইউ এবং আমি ওই মডেলের সংশোধিত পদের অসীম সেট নির্ণয় করেছিলাম।)

শেষ পর্যন্ত মূল বৈশিষ্ট্যটি শনাক্ত করতে পারেন শিকাগো বিশ্ববিদ্যালয়ের ইয়োচিরো নাম্বু এবং নিহন বিশ্ববিদ্যালয়ের টেটসুও গোতো। এটিই মডেলটিকে কার্যকর করে তোলে। এই বৈশিষ্ট্যটা হলো একটা ভাইব্রেটিং স্ট্রিং বা কম্পমান সুতা। (লিওনার্ড সাসকিন্ড এবং হোলগার নিয়েলসেনও ঠিক এই পথে কাজ করেছিলেন।) একটা স্ট্রিং যখন আরেকটা স্ট্রিংয়ের সঙ্গে সংঘর্ষের মুখে পড়ে, তখন তাতে একটা এস-ম্যাট্রিকস তৈরি হয়, যা ভেনেজিয়ানো মডেল দিয়ে ব্যাখ্যা করা যায়। এই মডেলে প্রতিটি কণা স্ট্রিংয়ের ওপর একটা কম্পন বা সুর ছাড়া আর কিছুই নয়। (এই ধারণা সম্পর্কে পরে আরও বিস্তারিত আলোচনা করব।)

বেশ দ্রুত এ বিষয়ে অগ্রগতি হতে লাগল। ১৯৭১ সালে এ স্ট্রিং মডেলকে সাধারণীকরণ করেন জন সোয়ার্জ, আন্দ্রেই নেভ্যু এবং পিয়েরে রেমন্ড। এতে স্পিন নামের নতুন এক সংখ্যা যুক্ত করা হলো। কণার মিথস্ক্রিয়ার জন্য বাস্তবসম্মত এক ধর্ম হিসেবে আবির্ভূত হয় এই স্পিন। (অচিরেই দেখতে পাব, সব অতিপারমাণবিক কণা এক ক্ষুদ্রাকৃতির লাটিমের মতো ঘুরছে বলে মনে হয়। কোয়ান্টাম এককে প্রতিটি অতিপারমাণবিক কণার এই স্পিন বা ঘূর্ণনের পরিমাণ হয় ০, ১, ২-এর মতো একটা পূর্ণ সংখ্যা, নয়তো ১/২, ৩/২-এর মতো অর্ধপূর্ণ সংখ্যা। লক্ষণীয় ব্যাপার হলো, নেভ্যু-সোয়ার্জ-রেমন্ডের স্ট্রিং থেকে নিখুঁতভাবে এই প্যাটার্নের স্পিন পাওয়া যায়।)

তবে আমি এখনো সন্তুষ্ট হতে পারিনি। তখন যাকে ডুয়েল রেজোনেন্স বা দ্বৈত অনুনাদী মডেল বলা হতো, সেটা কিছু অদ্ভুত সূত্রের আলগা গুচ্ছ এবং অভিজ্ঞতা ও অনুশীলনের ওপর ভিত্তি করে গড়ে ওঠা। আগের ১৫০ বছরের সব পদার্থবিজ্ঞান গড়ে উঠেছে ফিল্ড বা ক্ষেত্রের ওপর ভিত্তি করে। সেটা প্রথম চালু করেন ব্রিটিশ পদার্থবিদ মাইকেল ফ্যারাডে। এরপর থেকেই তা চলছে। একটা দণ্ড চুম্বকের মাধ্যমে গড়ে ওঠা চুম্বকীয় ক্ষেত্র রেখার কথা চিন্তা করুন। একটা মাকড়সার জালের মতো বলের রেখা সব জায়গায় ছড়িয়ে পড়ে। স্থানের প্রতিটি বিন্দুতে, চুম্বকীয় বল রেখার শক্তি ও দিক মাপা সম্ভব। একইভাবে একটা ক্ষেত্র হলো গাণিতিক কোনো বস্তু, যা স্থানের প্রতিটি বিন্দুতে ভিন্ন ভিন্ন মান অনুমান করে। কাজেই, ওই ক্ষেত্রটি মহাবিশ্বের যেকোনো বিন্দুতে চুম্বকীয়, বৈদ্যুতিক কিংবা পারমাণবিক বলের শক্তি মাপতে পারে। বৈদ্যুতিক, চুম্বকীয়, পারমাণবিক বল ও মহাকর্ষের মৌলিক ব্যাখ্যা এই ফিল্ড বা ক্ষেত্রের ওপর ভিত্তি করে গড়ে উঠেছে এই কারণে। তাহলে স্ট্রিং আলাদা হবে কেন? স্ট্রিংয়ের এমন একটা ফিল্ড থিওরি দরকার, যেটা এই তত্ত্বের সবগুলো বিষয়কে একটা মাত্র সমীকরণে সংক্ষিপ্তকরণ করতে পারবে।

১৯৭৪ সালে এ সমস্যা মোকাবিলা করার সিদ্ধান্ত নিই আমি। ওসাকা বিশ্ববিদ্যালয়ের আমার সহকর্মী কেইজি কিক্কাওয়ার সঙ্গে সফলভাবে স্ট্রিংয়ের ক্ষেত্র তত্ত্ব বের করে আনতে সক্ষম হই। প্রায় দেড় ইঞ্চি লম্বা এক সমীকরণে, স্ট্রিং থিওরিতে থাকা সব তথ্য সংক্ষেপে সংকলিত করতে পারি আমরা দুজন। স্ট্রিংয়ের ক্ষেত্র তত্ত্ব সূত্রবদ্ধ হয়ে যাওয়ার পর, আমি বৃহত্তর পদার্থবিজ্ঞান সম্প্রদায়কে এর শক্তি ও সৌন্দর্য বোঝাতে সক্ষম হই। সেই গ্রীষ্মে কলোরাডোর অ্যাসপেন সেন্টারে তাত্ত্বিক পদার্থবিজ্ঞানের এক কনফারেন্সে অংশ নিলাম। সেখানে এক সেমিনারের আয়োজন করি পদার্থবিদদের ছোট ও নির্বাচিত একটা দলের জন্য। আমি বেশ নার্ভাস ছিলাম। কারণ, দর্শকদের মধ্যে ছিলেন দুজন নোবেল বিজয়ী বিজ্ঞানী। তাঁরা মারে গেল-মান এবং রিচার্ড ফাইনম্যান। তীক্ষ্ণ আর ভয়ংকর প্রশ্ন করার ব্যাপারে তাঁরা ছিলেন কুখ্যাত। তাঁদের প্রশ্নের তোড়ে প্রায়ই হতবুদ্ধি হয়ে যান বক্তারা। (একবার দর্শকদের সামনে বক্তৃতা দিচ্ছিলেন স্টিভেন ওয়াইনবার্গ। ব্ল্যাকবোর্ডে তিনি একটা কোণ এঁকে সেটা ডব্লিউ বর্ণ দিয়ে চিহ্নিত করলেন। কারণ, তাঁর সম্মানে ওই কোণকে বলা হয় ওয়াইনবার্গ কোণ। ফাইনম্যান জিজ্ঞেস করলেন, ব্ল্যাকবোর্ডে লেখা ডব্লিউ দিয়ে কী বোঝাচ্ছে। ওয়াইনবার্গ উত্তর দিতে শুরু করতেই ফাইনম্যান চিৎকার করে বললেন, ‘রং!’। তাতে শিগগিরই হাসিতে ফেটে পড়লেন দর্শকেরা। ফাইনম্যান হয়তো দর্শকদের বিনোদিত করতে চেয়েছিলেন। কিন্তু সেবার আসলে শেষ হাসিটা হাসেন ওয়াইনবার্গ। এই কোণটি ওয়াইনবার্গের তত্ত্বের একটা গুরুত্বপূর্ণ অংশের প্রতীক, যা বিদ্যুৎ-চুম্বকীয় ও দুর্বল মিথস্ক্রিয়াকে একীভূত করে। এটাই একসময় পরে তাঁকে নোবেল পুরস্কার এনে দেয়।)

সেমিনারে আমার বক্তৃতায় জোরালোভাবে বললাম, স্ট্রিং থিওরির জন্য স্ট্রিং ফিল্ড থিওরি সবচেয়ে সরল ও সবচেয়ে সুসংহত পদ্ধতি এনে দেবে। কারণ, একসময় বিভিন্ন বিযুক্ত সূত্রগুলোর একটা বড় ধরনের বিচিত্র গুচ্ছ ছিল তত্ত্বটি। স্ট্রিং ফিল্ড থিওরির মাধ্যমে গোটা তত্ত্বকে দেড় ইঞ্চি দৈর্ঘ্যের একটা মাত্র সমীকরণের সংক্ষিপ্ত করা যাবে। এতে ভেনেজিয়ানো মডেলের সব বৈশিষ্ট্য, অসীম আসন্নতার সব পদ ও ঘূর্ণমান স্ট্রিংয়ের সবগুলো ধর্ম—এই ফরচুন কুকির ওপর এঁটে যাওয়া একটা সমীকরণ থেকে বের করে আনা সম্ভব। আমার বক্তৃতায় স্ট্রিং থিওরিতে সৌন্দর্য আর শক্তি দেওয়া প্রতিসাম্যতাগুলোর প্রতিও জোর দিলাম। স্থান-কালের মধ্যে যখন স্ট্রিংগুলো চলাফেরা করে, তারা দ্বিমাত্রিক তল (ফিতার সঙ্গে মিল আছে) থেকে বেরিয়ে আসে। এই দ্বিমাত্রিক তলকে বর্ণনা করতে কোনো স্থানাঙ্ক ব্যবহার করলেও এই তত্ত্ব একই থাকে। এর পরের ঘটনা আমি কখনো ভুলব না। ফাইনম্যান আমার কাছে এসে বললেন, “স্ট্রিং থিওরির পুরোটার সঙ্গে আমি হয়তো একমত নই, কিন্তু তুমি যে বক্তৃতা দিলে, সেটা আমার শোনা চমৎকার বক্তৃতাগুলোর একটি।’

দশ মাত্রা

স্ট্রিং থিওরি সফলতা পাওয়ার সঙ্গে সঙ্গে এর জটগুলোও খুলে যেতে লাগল বেশ দ্রুত। রগার্স বিশ্ববিদ্যালয়ের ক্লদ লাভলেস আবিষ্কার করলেন, ভেনেজিয়ানোর আদি মডেলে ছোট্ট একটা গাণিতিক ত্রুটি ছিল। এ ত্রুটি দূর করা সম্ভব, যদি স্থান-কালের মাত্রা ২৬টি হয়। একইভাবে নেভ্যু, সোয়ার্জ এবং রেমন্ডের সুপারস্ট্রিং মডেলও কেবল দশ মাত্রায় থাকা সম্ভব। এসব দেখে হতবাক হলেন পদার্থবিদেরা। বিজ্ঞানের গোটা ইতিহাসে আগে কখনো এমনটি দেখা যায়নি। কোনো তত্ত্ব নিজেই নিজের মাত্রা বেছে নিচ্ছে, এমনটি কোথাও খুঁজে পাওয়া যাবে না। যেমন নিউটন আর আইনস্টাইনের তত্ত্বগুলো সূত্রবদ্ধ করা যায় যেকোনো মাত্রায়। মহাকর্ষের বিখ্যাত বিপরীত বর্গীয় সূত্রকে চার মাত্রার মধ্যে বিপরীত ঘনকীয় সূত্র হিসেবে বিবৃত করা যায়। কিন্তু স্ট্রিং থিওরি কেবল থাকতে পারে নির্দিষ্ট মাত্রায়।

প্রায়োগিক দিক থেকে দেখলে, এটা একটা বিপর্যয়ই বটে। সর্বজনীনভাবে বিশ্বাস করা হয়, আমাদের বিশ্ব স্থানের তিন মাত্রা (দৈর্ঘ্য, প্রস্থ ও বেধ) এবং সময়ের একটা মাত্রায় বিরাজ করছে। সেখানে দশ মাত্রিক মহাবিশ্ব কবুল করার অর্থ, এই তত্ত্বটা আসলে বিজ্ঞান কল্পকাহিনির রাজ্যে ঢুকে পড়েছে। কাজেই স্বাভাবিকভাবে স্ট্রিং তাত্ত্বিকেরা হয়ে উঠলেন ঠাট্টা আর রসিকতার লক্ষ্যবস্তু। (জন সোয়ার্জ একবার রিচার্ড ফাইনম্যানের সঙ্গে একই এলিভেটরে চড়েছিলেন। রসিকতার সুরে ফাইনম্যান তাঁকে বললেন, “আচ্ছা, জন, তুমি আজকে ঠিক কত মাত্রায় আছ?’) তবে স্ট্রিং পদার্থবিদেরা এই মডেলটাকে যতই উদ্ধারের চেষ্টা করুক না কেন, তা শিগগিরই মৃত্যুমুখে পতিত হলো। এই তত্ত্ব নিয়ে গবেষণা চালিয়ে গেলেন শুধু প্রচণ্ড জেদি আর আপসহীন গুটি কয়েকজন। সে সময় সেটা ছিল নিঃসঙ্গ এক প্রচেষ্টা।

সেই বিষণ্ন ও হতাশাব্যঞ্জক সময়ে এই তত্ত্বের ওপর গবেষণা চালিয়ে যাওয়া দুজন আপসহীন বিজ্ঞানী হলেন যুক্তরাষ্ট্রের ক্যাল টেকের জন সোয়ার্জ এবং প্যারিসের ইকোল নরমেল সুপারিরির জোয়েল শার্ক। এরপর থেকে এই স্ট্রিং মডেলটি শুধু শক্তিশালী নিউক্লিয়ার মিথস্ক্রিয়া ব্যাখ্যা করতে পারত বলে মনে করা হতো। কিন্তু এতে একটা সমস্যাও ছিল : মডেলটি এমন একটা কণার ভবিষ্যদ্বাণী করল, যা শক্তিশালী মিথস্ক্রিয়ায় ঘটতে দেখা যায় না। সেটা চমকপ্রদ একটা কণা, যার ভর শূন্য, যার স্পিন দুই কোয়ান্টাম একক। বিরক্তিকর এই কণাটির বাতিল করার সব রকম চেষ্টাই বিফলে গেল। যতবারই স্পিন-২ যুক্ত কণাটিকে দূর করার চেষ্টা চালানো হয়, ততবারই মডেলটি ভেঙে যায়। সেই সঙ্গে হারিয়ে যায় তার ম্যাজিক্যাল বৈশিষ্ট্যগুলোও। কোনোভাবে এই অবাঞ্ছিত স্পিন-২ কণাটিই যেন গোটা মডেলটার গোপনীয়তা ধরে রেখেছে বলে মনে হলো।

এরপর এক দুঃসাহসিক অনুমান করে বসলেন শার্ক এবং সোয়ার্জ। হয়তো এই ত্রুটিই আসলে তাদের জন্য আশীর্বাদও হয়ে উঠতে পারে। এই ক্লান্তিকর স্পিন-২ সম্পন্ন কণাটিকে যদি গ্রাভিটন হিসেবে ধরে নেওয়া যায়, তাহলে তত্ত্বটিকে আইনস্টাইনের মহাকর্ষ সূত্রের সঙ্গে যোগসূত্র তৈরি করা সম্ভব (গ্রাভিটন হলো গ্রাভিটি বা মহাকর্ষের কণা, যা আইনস্টাইনের সূত্র থেকে আসে)! (অন্য কথায়, সুপারস্ট্রিংয়ের সর্বনিম্ন কম্পন বা সুর থেকে আইনস্টাইনের সাধারণ আপেক্ষিকতা সরলভাবে আবির্ভূত হয়। ) মজার ব্যাপার হলো, অন্য কোয়ান্টাম তত্ত্বগুলোতে পদার্থবিদেরা মহাকর্ষের উল্লেখ না করতে পারার কারণে মাথার ঘাম পায়ে ফেলছিলেন। কিন্তু দেখা গেল স্ট্রিং থিওরি সহজাতভাবে মহাকর্ষ দাবি করে। (আসলে এটাই স্ট্রিং থিওরির অন্যতম আকর্ষণীয় বৈশিষ্ট্য। অর্থাৎ এতে অনিবার্যভাবে মহাকর্ষ যোগ করতে হবে, নয়তো তত্ত্বটি হয়ে ওঠে বেমানান।) দুঃসাহসিক একটা লাফে বিজ্ঞানীরা বুঝতে পারলেন, স্ট্রিং মডেল ভুলভাবে ভুল সমস্যায় প্রয়োগ করা হয়েছে। এটা শুধু সবল নিউক্লিয়ার মিথস্ক্রিয়ার তত্ত্ব নয়, বরং সবকিছুর তত্ত্ব (থিওরি অব এভরিথিং)। উইটেন জোর দিয়ে বলেছেন, স্ট্রিং থিওরির অন্যতম চমকপ্রদ বৈশিষ্ট্য হলো এটা মহাকর্ষের উপস্থিতি দাবি করে। স্ট্যান্ডার্ড ফিল্ড থিওরিগুলো দশকের পর দশক যখন মহাকর্ষকে অন্তর্ভুক্ত করতে ব্যর্থ হয়েছে, সেখানে স্ট্রিং থিওরিতে মহাকর্ষ থাকা বাধ্যতামূলক।

তবে শার্ক ও সোয়ার্জের এই গুরুত্বপূর্ণ ধারণাটি সর্বজনীনভাবে উপেক্ষিত হয়েছিল। স্ট্রিং থিওরি একই সঙ্গে মহাকর্ষ এবং অতিপারমাণবিক জগৎকে ব্যাখ্যা করে। তাই এর মানে, স্ট্রিংগুলোকে লম্বায় হতে হবে মাত্র ১০^-৩৩ সেমি (প্ল্যাঙ্ক দৈর্ঘ্য)। সহজ কথায়, এদের দৈর্ঘ্য হবে একটা প্রোটনের চেয়ে বিলিয়ন বিলিয়ন ভাগ ছোট। সে সময় অধিকাংশ বিজ্ঞানীর পক্ষে এটা মেনে নেওয়া কঠিন ছিল।

কিন্তু ১৯৮০-এর দশকের মাঝামাঝিতে একটা ইউনিফায়েড ফিল্ড থিওরি প্রণয়নের অন্য সব প্রচেষ্টা বারবার হোঁচট খাচ্ছিল। যেসব তত্ত্বে মহাকর্ষকে স্ট্যান্ডার্ড মডেলের সঙ্গে সরলভাবে সংযুক্ত করার চেষ্টা করা হচ্ছিল, সেগুলো যেন অসীমের জলাভূমিতে ডুবে যাচ্ছিল (এটা কিছুক্ষণের মধ্যেই ব্যাখ্যা করব)। মহাকর্ষকে যখনই কেউ অন্যান্য কোয়ান্টাম বলের সঙ্গে কৃত্রিমভাবে গাঁটছড়া বাঁধার চেষ্টা করছিল, তখনই তা গাণিতিকভাবে বেমানান হয়ে যাচ্ছিল। হত্যা করা হচ্ছিল তত্ত্বটিকে। (আইনস্টাইন বিশ্বাস করতেন, মহাবিশ্ব সৃষ্টির বেলায় ঈশ্বরের হয়তো কোনো কিছু বেছে নেওয়ার সুযোগ ছিল না। একটা কারণে এটা হতে পারে যে শুধু একটামাত্র তত্ত্ব সবগুলো গাণিতিকভাবে অসংগতি থেকে মুক্ত ছিল।)

দুই ধরনের গাণিতিক অসংগতি ছিল সেখানে। প্রথমটি হলো অসীমের সমস্যা। সাধারণত কোয়ান্টাম ফ্ল্যাকচুয়েশন খুব ছোট। কোয়ান্টাম প্রভাব সাধারণত নিউটনের গতির সূত্রগুলোকে সংশোধন করে খুব অল্পই। তাই অধিকাংশ ক্ষেত্রে ম্যাক্রোস্কোপিক বা বৃহৎ পরিসরের জগতে তাদের নাকচ করা যায়। কারণ, সেগুলো এতই ছোট যে তা নজরেই পড়ে না। তবে মহাকর্ষ যখন কোয়ান্টাম থিওরিতে পরিণত হয়, তখন এসব কোয়ান্টাম ফ্ল্যাকচুয়েশন অসীমে পরিণত হয়, যা আসলে অর্থহীন। দ্বিতীয় গাণিতিক অসংগতিটি ছিল অস্বাভাবিকতা। এটা তত্ত্বের ছোট ধরনের বিচ্যুতি। কোনো তত্ত্বে যখন কোয়ান্টাম ফ্ল্যাকচুয়েশন যোগ করা হয়, তখন এটা দেখা যায়। এই অস্বাভাবিকতা তত্ত্বটির আদি প্রতিসাম্যতা নষ্ট করে ফেলে। তার ফলে এর আসল শক্তিও হারিয়ে যায়।

উদাহরণস্বরূপ একটা রকেট ডিজাইনারের কথা ভাবুন। একে অবশ্যই এমন একটা মসৃণ, চকচকে গতিময় যান বানাতে হবে। বায়ুমণ্ডলকে ফালি করে কেটে ওপরে উঠে যেতে যাতে সমস্যা না হয়। বাতাসের ঘর্ষণ ও ধাক্কা কমিয়ে আনার জন্য রকেটটিকে অবশ্যই চরম প্রতিসাম্য করে বানাতে হবে (এ ক্ষেত্রে সিলিন্ডার আকৃতির প্রতিসাম্যতা দরকার, যাতে রকেটটিকে তার অক্ষের চারপাশে ঘোরালেও একই থাকে)। এই প্রতিসাম্যতাকে বলা হয় O(2)। কিন্তু এখানে সম্ভাব্য দুটি সমস্যা আছে। প্রথমটি হলো, রকেটটি বিপুল গতিতে চলার কারণে তার পাখায় কম্পনের সৃষ্টি হতে পারে। সাধারণত সাবসনিক (শব্দের গতির চেয়ে কম) বিমানগুলোতে এই কম্পন বেশ কম। তবে হাইপারসনিক (শব্দের গতির চেয়ে বেশি) বেগে চলতে গেলে এই ফ্ল্যাকচুয়েশন বেড়ে যেতে পারে তীব্রভাবে। ফলে পাখা দুটিও একসময় ভেঙে যেতে পারে। একইভাবে মহাকর্ষের যেকোনো কোয়ান্টাম তত্ত্বে বিপর্যয় ঘটায় বিচ্যুতি। স্বাভাবিকভাবে, এগুলো এতই অল্প যে তাদের অগ্রাহ্য করা চলে। কিন্তু মহাকর্ষের কোয়ান্টাম তত্ত্বে আপনার মুখ উড়িয়ে দেওয়ার জন্য সেগুলো যথেষ্ট।

রকেট শিপের দ্বিতীয় সমস্যাটি হলো, এটি কাঠামোতে ক্ষুদ্র ফাটলের সৃষ্টি করতে পারে। এই ত্রুটি রকেট শিপের আসল O(2) প্রতিসাম্যতাকে ফেলে দিতে পারে এক বিপর্যয়ের মুখে। এটি যত ক্ষুদ্রই হোক না কেন, এই ত্রুটিই ধীরে ধীরে ছড়িয়ে পড়ে রকেটের কাঠামোকে টুকরো টুকরো করে ভেঙেও ফেলতে পারে। একইভাবে এ ধরনের কোনো ‘ফাটল’ মহাকর্ষ তত্ত্বের প্রতিসাম্যতার জন্য মৃত্যু ডেকে আনার শামিল।

এই সমস্যা সমাধানের দুটি উপায় আছে। প্রথমটি হলো একটা ব্যান্ড- এইড সমাধান খোঁজ করা। অর্থাৎ ফাটলকে আঠা দিয়ে মেরামত করা। পাশাপাশি লাঠি দিয়ে পাখা দুটোকে শক্ত করে বেঁধে একটা অবলম্বন দেওয়া। এর মাধ্যমে আশা করা হয় যে রকেটটি আর বায়ুমণ্ডলে বিস্ফোরিত হবে না। ঐতিহাসিকভাবে এই পদ্ধতি ব্যবহার করে কোয়ান্টাম তত্ত্বের সঙ্গে মহাকর্ষের মেলবন্ধনের চেষ্টা করেছেন অধিকাংশ পদার্থবিজ্ঞানী। এই সমস্যা দুটিকে মোটা চাদরের নিচে রেখে ঘষামাজা করার চেষ্টা চলেছে। দ্বিতীয় পদ্ধতিটি হলো, সবকিছু আবারও নতুন করে শুরু করা। অর্থাৎ নতুন আকৃতি ও নতুন চমকপ্রদ কোনো উপাদান ব্যবহার করা, যা মহাকাশ ভ্রমণের চাপ সহ্য করতে পারবে। মহাকর্ষের একটা কোয়ান্টাম তত্ত্ব জোড়াতালি দেওয়ার চেষ্টায় দশকের পর দশক ব্যয় করেছেন পদার্থবিজ্ঞানীরা। কিন্তু তার বিনিময়ে হতাশাজনকভাবে নতুন নতুন বিচ্যুতি আর অস্বাভাবিকতা ধাঁধার খোঁজ পাওয়া গেছে। ক্রমেই তাঁরা বুঝতে পেরেছেন, এই সমাধান থেকে ব্যান্ড-এইড পদ্ধতি বাদ দিয়ে সম্পূর্ণ নতুন কোনো তত্ত্ব খুঁজে বের করতে হবে।

স্ট্রিংয়ের শোভাযাত্রা

মজার ব্যাপার হলো, ১৯৮৪ সালে স্ট্রিং থিওরির বিরুদ্ধ স্রোত হুট করেই উল্টে গেল। ক্যালটেকের জন সোয়ার্জ এবং তৎকালে লন্ডনের কুইন মেরিজ কলেজের মাইক গ্রিন দেখালেন, স্ট্রিং থিওরি সব রকম অসংগতিবর্জিত। এই অসংগতিই যুগে যুগে হত্যা করেছিল অন্য বেশ কিছু তত্ত্বকে। পদার্থবিদেরা আগে থেকেই জানতেন, স্ট্রিং থিওরি গাণিতিক বিচ্যুতি থেকে মুক্ত। কিন্তু সোয়ার্জ ও গ্রিন দেখালেন, এটা অস্বাভাবিকতা থেকেও মুক্ত। ফলে থিওরি অব এভিরিথিংয়ের শীর্ষস্থানীয় (বর্তমানেও একমাত্র) পদপ্রার্থী হয়ে ওঠে স্ট্রিং থিওরি।

এককালে যে তত্ত্বটাকে অনিবার্যভাবে মৃত বলে মনে করা হতো, হঠাৎ করে সেটাই বেঁচে উঠল নতুনভাবে। এভাবে একটা থিওরি অব নাথিং থেকে শিগগিরই থিওরি অব এভরিথিং হয়ে উঠল স্ট্রিং থিওরি। অসংখ্য পদার্থবিদ মরিয়া হয়ে স্ট্রিং থিওরিসংক্রান্ত পেপারগুলো পড়ার আপ্রাণ চেষ্টা করতে লাগলেন। সারা বিশ্বের গবেষণা ল্যাবরেটরি থেকে এ বিষয়ে লেখা পেপার ঝরে পড়তে লাগল তুষারধসের মতো। লাইব্রেরিগুলোতে পুরোনো যেসব পেপারে এত দিনে ধুলোকণার পুরো স্তূপ জমে উঠেছিল, আচমকা সেগুলোই হয়ে উঠল পদার্থবিদ্যার সবচেয়ে উত্তেজক বিষয়বস্তুতে। প্যারালাল ওয়ার্ল্ড বা সমান্তরাল মহাবিশ্বের যে আইডিয়াকে একসময় বিদঘুটে বলে ভাবা হতো, সেটাই তখন হয়ে উঠল পদার্থবিজ্ঞান সম্প্রদায়ের আলোচনার কেন্দ্ৰবিন্দু। শত শত কনফারেন্স এবং আক্ষরিক অর্থে হাজারো পেপার লেখা হতে লাগল এই বিষয়কে ঘিরে।

(১৯৯১ সালের আগস্টে গুটি কয়েক পদার্থবিদ ‘নোবেলজ্বরে’ আক্রান্ত হলেন। ডিসকভার ম্যাগাজিনও প্রচ্ছদজুড়ে উত্তেজক শিরোনাম যোগ করল, ‘দ্য নিউ থিওরি অব এভরিথিং: আ ফিজিসিস্ট ট্যাকলস দ্য আলটিমেট কসমিক রিডল।’ প্রবন্ধটিতে খ্যাতি আর গৌরব অর্জনের সাধনায় থাকা এক পদার্থবিদের উদ্ধৃতি যোগ করা হলো। তিনি বড়াই করে বললেন, ‘আমি বিনয়ী কেউ নই। এ তত্ত্বটা কাজ করলে, এতে একটা নোবেল পুরস্কার পাওয়া যাবে।’ স্ট্রিং থিওরি এখনো তার শৈশব অবস্থায় আছে—এমন সমালোচনার মুখে তিনি পাল্টা গুলি ছুড়ে বললেন, “বড় বড় স্ট্রিং ব্যক্তিত্বরা বলছেন, স্ট্রিংয়ের প্রমাণের জন্য চার শ বছর লাগবে। কিন্তু আমি বলি, তাঁদের চুপ থাকা উচিত।’)

শিগগিরই একটা গোল্ড রাশ শুরু হলো। সোনার খোঁজে দিশেহারা হয়ে পড়িমরি করে ছুটতে লাগল সবাই।

একসময় এই ‘সুপারস্ট্রিং শোভাযাত্রার বাদকদলের’ বিরুদ্ধে সমালোচনার ঝড় ওঠে। হার্ভার্ডের এক পদার্থবিদ বিদ্রূপ করে বলেন, স্ট্রিং থিওরি আসলে পদার্থবিজ্ঞানের কোনো শাখা নয়, এটা যদি ধর্মেরও কোনো শাখা না হয়, তাহলে বিশুদ্ধ গণিতের কিংবা দর্শনের শাখা। অভিযোগের নেতৃত্বে এসে হার্ভার্ডের নোবেল বিজয়ী শেলডন গ্ল্যাসো সুপারস্ট্রিং শোভাযাত্রার বাদকদলকে স্টার ওয়ার্স অনুষ্ঠানের সঙ্গে তুলনা করলেন (স্টার ওয়ার্সেও অনেক উৎস দেখানো হয়, কিন্তু কোনোটাই পরীক্ষা করে দেখা যায় না)। গ্ল্যাসো বললেন, অনেক তরুণ পদার্থবিদ স্ট্রিং থিওরিতে কাজ করছে দেখে তিনি বেশ খুশি। কারণ, এর ফলে তারা তাঁর কাছ থেকে শত হাত দূরে থাকতে পারছে। উইটেন একবার মন্তব্য করেছিলেন, বিগত পঞ্চাশ বছর কোয়ান্টাম মেকানিকস যেমন পদার্থবিজ্ঞানকে শাসন করেছে, তেমনি আগামী পঞ্চাশ বছর স্ট্রিং থিওরি হয়তো পদার্থবিজ্ঞানকে শাসন করবে। এ ব্যাপারে গ্ল্যাসোর কাছে মন্তব্য চাওয়া হলে তিনি বললেন, স্ট্রিং থিওরি পদার্থবিজ্ঞানকে সেভাবেই শাসন করবে, যেমনটা কালুজা-ক্লেইন থিওরি (যাকে পাগলাটে অর্থহীন বলে মনে করা হতো) গত পঞ্চাশ বছর করেছিল। আসলে এই তত্ত্ব তা করতে পারেনি। স্ট্রিং তাত্ত্বিকদের হার্ভার্ড থেকে বাইরে রাখার চেষ্টা করা হতো। কিন্তু পরের প্রজন্মের পদার্থবিদেরা স্ট্রিং থিওরি আঁকড়ে ধরতে শুরু করার সঙ্গে সঙ্গে তাতে কোনো কোনো নোবেল বিজয়ী বিজ্ঞানীর নিঃসঙ্গ কণ্ঠস্বর হারিয়ে যেতে লাগল। (তারপর থেকে বেশ কয়েকজন তরুণ স্ট্রিং তাত্ত্বিককে নিয়োগ দেয় হার্ভার্ড বিশ্ববিদ্যালয়। )

মহাজাগতিক সংগীত

আইনস্টাইন একবার বলেছিলেন, কোনো তত্ত্ব যদি একটা শিশুর বোঝার মতো কোনো ভৌত চিত্র হাজির করতে না পারে, তাহলে ওটা আসলে অর্থহীন। সৌভাগ্যক্রমে স্ট্রিং থিওরির পেছনে একটা সরল ভৌত চিত্র আছে। সেটা এমন একটা চিত্র, যার ভিত্তি সংগীত।

স্ট্রিং থিওরি অনুসারে, আপনার কাছে যদি একটা সুপারমাইক্রোস্কোপ থাকে এবং তা দিয়ে যদি কোনো ইলেকট্রনের মাঝখানে উঁকি দেওয়া সম্ভব হয়, তাহলে সেখানে কোনো বিন্দু কণা নয়, বরং একটা কম্পনশীল স্টিং বা সুতা হিসেবে দেখা যাবে। (এই স্ট্রিং এতই খুদে যে তা একটা প্রোটনের চেয়ে এক বিলিয়ন বিলিয়ন ভাগ ছোট। এটি প্ল্যাঙ্ক দৈর্ঘ্যের সমান ১০^-৩৩ সেন্টিমিটার। কাজেই সব অতিপারমাণবিক কণাকে বিন্দুর মতো দেখা যায়।) আমরা যদি এই সুতায় টান দিতে পারতাম, তাহলে এর কম্পন হয়তো বদলে যেত। তখন ইলেকট্রনটা হয়তো রূপান্তরিত হতো একটা নিউট্রিনো কণায়। একে আবারও টানা হলে, সেটা হয়তো একটা কোয়ার্কে রূপান্তরিত হতো। আসলে আপনি একে যত জোরেই টান মারুন না কেন, তা আমাদের জানা কোনো না কোনো অতিপারমাণবিক কণায় বদলে যাবে। এভাবে স্ট্রিং থিওরি অনায়াসে ব্যাখ্যা করতে পারে—অতিপারমাণবিক কণার সংখ্যা এত বেশি কেন। এখানে আসলে ‘সুর’ ছাড়া আর কিছু নেই। আর এই সুর বাজানো যায় একটা সুপারস্ট্রিংয়ে। একে একটা ভায়োলিনের তারের ওপর A বা B বা C শার্পের সঙ্গে তুলনা করা যায়, যারা মৌলিক নয়। এই তারগুলো সহজভাবে বিভিন্নভাবে প্লাকিং করে বা টেনে, সংগীতের সব সুর সৃষ্টি করা যায়। যেমন B ফ্ল্যাট G-এর চেয়ে খুব বেশি মৌলিক নয়। তাদের সবগুলোই একটা বেহালার তারের ওপর সুর ছাড়া আর কিছু নয়। একইভাবে ইলেকট্রন ও কোয়ার্কও মৌলিক নয়, বরং স্ট্রিংই হলো মৌলিক। আসলে মহাবিশ্বের সব উপকণাকে তারের ওপর ভিন্ন ভিন্ন কম্পন হিসেবে দেখা যায়। এসব স্ট্রিংয়ের হারমনি বা ঐকতান হলো পদার্থবিজ্ঞানের সূত্র।

স্ট্রিং টুকরো টুকরো হয়ে এবং আবার একত্র হয়ে মিথস্ক্রিয়া করতে পারে। এভাবে যে মিথস্ক্রিয়ার সৃষ্টি হয়, সেগুলোই আমরা পরমাণুর ভেতরে ইলেকট্রন, প্রোটনে দেখতে পাই। এই পদ্ধতিতে স্ট্রিং থিওরির ভেতর দিয়ে আমরা পারমাণবিক ও নিউক্লিয়ার পদার্থবিজ্ঞানের সব সূত্র নতুন করে পেতে পারি। তারের ওপর যে মেলোডি লেখা থাকে, সেটা রসায়নের সূত্রের সঙ্গে সংশ্লিষ্ট। আর মহাবিশ্বকে এখন একটা তারের ওপর বিশাল এক সিম্ফনি হিসেবে দেখা যেতে পারে।

স্ট্রিং থিওরি শুধু কোয়ান্টাম তত্ত্বের কণাগুলোকে মহাবিশ্বের মিউজিক্যাল নোট হিসেবে দেখে তা-ই নয়, এটা আইনস্টাইনের আপেক্ষিক তত্ত্বকেও ব্যাখ্যা করতে পারে। তারের সর্বনিম্ন কম্পন হিসেবে, দুই স্পিন যুক্ত কণা, যার ভর শূন্য, যাকে গ্র্যাভিটন কণা হিসেবে ব্যাখ্যা করা যায়। গ্র্যাভিটনকে বলা হয় মহাকর্ষের কোয়ান্টাম বা কণা। আমরা যদি এসব গ্র্যাভিটনের মিথস্ক্রিয়া গণনা করি, তাহলে আইনস্টাইনের পুরোনো মহাকর্ষের তত্ত্বকে কোয়ান্টাম রূপে পাওয়া যাবে। স্ট্রিং যখন চলাফেরা করে এবং ভেঙে আবারও নতুন করে গঠিত হয়, তখন তা স্থান-কালে বিপুল বিধিনিষেধ আরোপ করে। এসব সীমাবদ্ধতা বিশ্লেষণ করলে আবারও আইনস্টাইনের পুরোনো সাধারণ আপেক্ষিক তত্ত্ব খুঁজে পাওয়া যায়। কাজেই স্ট্রিং থিওরি কোনো বাড়তি কাজ ছাড়াই পরিচ্ছন্নভাবে আইনস্টাইনের তত্ত্ব ব্যাখ্যা করে। এডওয়ার্ড উইটেন একবার বলেছিলেন, আইনস্টাইন যদি কখনো আপেক্ষিকতা আবিষ্কার না-ও করতেন, তাহলে তাঁর তত্ত্বটি স্ট্রিং থিওরির উপজাত হিসেবে আবিষ্কৃত হতো। সেই অর্থে সাধারণ আপেক্ষিকতা পাওয়া যেত একেবারে বিনা মূল্যে।

স্ট্রিং থিওরির সৌন্দর্য হলো, একে সংগীতের সঙ্গে তুলনা করা যায়। এখানে সংগীত একটা মেটাফোর বা রূপকের জোগান দেয়, যার মাধ্যমে আমরা একই সঙ্গে অতিপারমাণবিক পরিসর এবং মহাজাগতিক পরিসরে মহাবিশ্বের প্রকৃতি বুঝতে পারি। নামকরা বেহালাবাদক ইয়েহুদি মেনুহিন একবার লিখেছিলেন, ‘বিশৃঙ্খলা থেকে শৃঙ্খলা বের করে আনে সংগীত। বিচ্যুতির ওপর ছন্দ আরোপ করে, বিযুক্ততার ওপর অবিরাম মেলোডি আরোপ করে। আবার বেখাপ্পা কোনো কিছুর ওপর আরোপ করে সুসংগত হারমনি বা ঐকতান।

আইনস্টাইন হয়তো লিখতেন, ইউনিফায়েড ফিল্ড থিওরির জন্য তাঁর এত দিনের অনুসন্ধান শেষ পর্যন্ত তাঁকে ‘ঈশ্বরের মন পড়ার’ অনুমতি দিয়েছে। স্ট্রিং থিওরি সঠিক হলে আমরা এখন দেখব যে ঈশ্বরের মন মহাজাগতিক সংগীতের প্রতীক, যা দশ মাত্রিক উচ্চতর স্থানে অনুরণিত হচ্ছে। গডফ্রিড লিবনিজ একবার বলেছিলেন, ‘সংগীত হলো আত্মার গুপ্ত গাণিতিক চর্চা। একে যে গণনা করা হচ্ছে, সে ব্যাপারে তা অসচেতন।’

ঐতিহাসিকভাবে সংগীত ও বিজ্ঞানের মধ্যে সম্পর্ক প্রতিষ্ঠিত হয়েছিল সেই খ্রিষ্টপূর্ব পঞ্চম অব্দে। গ্রিক পিথাগোরিয়ান অনুসারীরা হারমনির সূত্র আবিষ্কার করল। সেগুলোকে ব্যাখ্যাও করল গাণিতিকভাবে। তারা দেখতে পেল, লায়ার তার টানলে যে স্বর পাওয়া যায়, তা তারের দৈর্ঘ্যের সঙ্গে সম্পর্কিত। লায়ার তারের দৈর্ঘ্য দ্বিগুণ করা হলে সুরটা একটা পুরো অষ্টক নিচে চলে যায়। আবার তারের দৈর্ঘ্য দুই-তৃতীয়াংশ কমানো হলে স্বর পাল্টে পঞ্চমে চলে যায়। কাজেই সংগীত ও হারমনির সূত্র নিখুঁতভাবে সংখ্যার সঙ্গে সম্পর্কিত বলে দেখা গেল। তাই অবাক হওয়ার কিছু নেই, পিথাগোরিয়ানদের মূলমন্ত্র ছিল, ‘সবকিছুই সংখ্যা।’ আসলে এই ফলাফলে তারা এতই খুশি হয়েছিল যে হারমনির এই সূত্রকে তারা গোটা মহাবিশ্বে প্রয়োগ করার দুঃসাহস দেখিয়েছিল। অবশ্য শেষ পর্যন্ত বিফলে গিয়েছিল তাদের সেই প্রচেষ্টা। তার পেছনের কারণ ছিল বস্তুর বিপুল জটিলতা। তবে এক অর্থে স্ট্রিং থিওরি সঙ্গে নিয়ে এখন পিথাগোরিয়ানদের সেই স্বপ্নের কাছেই যেন ফিরে গেছেন পদার্থবিদেরা।

ঐতিহাসিক এই যোগসূত্র সম্পর্কে জেমি জেমস একবার মন্তব্য করেন, ‘সংগীত ও বিজ্ঞান (একসময়) একেবারে অভিন্ন বলে গণ্য করা হতো। তাই যারা বলত, তাদের মধ্যে পার্থক্য আছে, তাদের অজ্ঞ ভাবা হতো। কিন্তু এখন কেউ যদি প্রস্তাব করে, তাদের মধ্যে কোনো সাধারণ ব্যাপার আছে, তাহলে তাকে মূর্খ হিসেবে চিহ্নিত করে বসতে পারে একদল। আর আরেক দল তাকে অনুরাগী হিসেবে আখ্যায়িত করবে। সবচেয়ে মারাত্মক ব্যাপার হলো, উভয় দলই জনপ্ৰিয়।’

হাইপারস্পেসের সমস্যা

কিন্তু উচ্চতর মাত্রা শুধু বিশুদ্ধ গণিতে সীমাবদ্ধ না থেকে যদি সত্যিই প্রকৃতিতে বিরাজ করে, তাহলে স্ট্রিং তাত্ত্বিকেরা আবারও একই ধরনের সমস্যার মুখোমুখি হবেন। ১৯২১ সালে যেমন সমস্যায় পড়েছিলেন থিওডর কালুজা এবং ফেলিক্স ক্লেইন। সে সময় প্রথমবার উচ্চতর মাত্রিক তত্ত্ব সূত্রবদ্ধ করতে গিয়ে এ সমস্যার মুখে পড়েন এই দুই বিজ্ঞানী। সমস্যাটি হলো : ওই সব উচ্চতর মাত্রা কোথায় আছে?

এককালের অখ্যাত গণিতবিদ কালুজা একবার আইনস্টাইনকে এক চিঠিতে আইনস্টাইনের সমীকরণ পাঁচ মাত্রার সূত্রবদ্ধ করার প্রস্তাব দেন (এই পাঁচটির মধ্যে একটি সময়ের আর চারটি স্থানের মাত্রা)। গাণিতিকভাবে এটা কোনো সমস্যাই নয়। কারণ, আইনস্টাইনের সমীকরণ অনায়াসে যেকোনো মাত্রায় লেখা সম্ভব। কিন্তু ওই চিঠিতে একটা অভিনব পর্যবেক্ষণ ছিল : হাতে- কলমে পঞ্চমাত্রিক সমীকরণের মধ্যে থাকা চার মাত্রিক টুকরোগুলো আলাদা করা হলে স্বয়ংক্রিয়ভাবে বা অনেকটা ম্যাজিকের মতো ম্যাক্সওয়েলের আলোর তত্ত্ব পাওয়া যায়! অন্য কথায়, আমরা যদি একটা পঞ্চম মাত্রা যোগ করি, তাহলে ম্যাক্সওয়েলের বিদ্যুৎ-চুম্বকীয় বলের তত্ত্বটি আইনস্টাইনের মহাকর্ষ সমীকরণ থেকে লাফ দিয়ে বেরিয়ে আসে। আমরা পঞ্চম মাত্রা চোখে দেখতে না পারলেও পঞ্চম মাত্রায় তরঙ্গ গঠিত হতে পারে, যা আলোকতরঙ্গের সঙ্গে মিলে যায়! এটি বেশ সন্তোষজনক ফল। কারণ, ১৫০ বছর ধরে বেশ কয়েক প্রজন্ম পদার্থবিদ আর ইঞ্জিনিয়ারদের ম্যাক্সওয়েলের কঠিন সূত্রগুলো মুখস্থ করতে হয়েছে। এখন এই জটিল সমীকরণগুলো পঞ্চম মাত্রার ভেতরে সরলতম কম্পনে অনায়াসে বেরিয়ে আসতে লাগল।

একটা অগভীর পুকুরে পদ্মফুলের পাতার নিচে একটা মাছের সাঁতার কাটার কথা কল্পনা করুন। তাদের মহাবিশ্ব মাত্র দুই মাত্রার বলে ধরে নিন। আমাদের ত্রিমাত্রিক বিশ্ব হয়তো তাদের দৃষ্টিসীমা বা জ্ঞানের বাইরে। কিন্তু একটা উপায়ে তারা তৃতীয় মাত্রার উপস্থিতি শনাক্ত করতে পারবে। বৃষ্টি পড়ার সময়, বেশ স্পষ্টভাবে ঢেউয়ের ছায়া পুকুরের পৃষ্ঠতলে চলাফেরা করতে দেখতে পাবে মাছগুলো। একইভাবে আমরাও পঞ্চম মাত্রা দেখতে পাই না। কিন্তু পঞ্চম মাত্রার ঢেউ বা তরঙ্গ আমাদের কাছে প্রকাশিত হয় আলো হিসেবে।

(কালুজার তত্ত্ব প্রতিসাম্যতার শক্তি বিষয়ে একটা চমৎকার ও গভীর এক উদ্‌ঘাটন। এটিই পরে প্রমাণ করে যে আইনস্টাইনের পুরোনো তত্ত্বে আরও মাত্রা যোগ করা হলে এবং সেগুলোকে কম্পনশীল করা হলে, এসব উচ্চতর মাত্রার কম্পন দুর্বল ও শক্তিশালী নিউক্লিয়ার বলগুলোর মধ্যে থাকা ডব্লিউ ও জেড বোসন এবং গ্লুয়নের প্রতিরূপ তৈরি করবে! কালুজার প্রস্তাবিত এই কর্মসূচি সঠিক হলে মহাবিশ্ব আমাদের আগের ভাবনার চেয়েও অনেক বেশি সরল হিসেবে প্রতিভাত হবে। উচ্চতর ও উচ্চতর মাত্রায় শুধু কম্পনের কারণে এই বিশ্বকে নিয়ন্ত্রণকারী অনেক বলের প্রতিরূপ গঠিত হতে পারে।)

এই ফলে বেশ হতবাক হয়েছিলেন খোদ আইনস্টাইনও। কিন্তু এটা দেখতে বেশ চমৎকার মনে হলেও এতে কিছু সমস্যাও ছিল। বেশ কয়েক বছর বেশ কিছু সমস্যা আবিষ্কৃত হয় এবং একসময় কালুজার ধারণাটি অকেজো করে তোলে। প্রথমত তত্ত্বটি বিচ্যুতি আর অস্বাভাবিকতাসহ বেশ কিছু ধাঁধার জন্ম দেয়। সেগুলো কোয়ান্টাম মহাকর্ষ তত্ত্বগুলোর জন্য সাধারণ এক বৈশিষ্ট্য। দ্বিতীয়ত এখানে বেশ কিছু বিব্রতকর ভৌত প্রশ্নও উঠে আসে : আমরা পঞ্চম মাত্রা দেখতে পাই না কেন? আকাশের দিকে তির ছোড়া হলে তা অন্য মাত্রায় অদৃশ্য হয়ে যায় না কেন? ধোঁয়ার কথা চিন্তা করুন। এরা ধীরে ধীরে ছড়িয়ে পড়ে স্থানের প্রতিটি অঞ্চলে। ধোঁয়াকে কখনোই উচ্চতর কোনো মাত্রায় হারিয়ে যেতে দেখা যায় না। তাই পদার্থবিদেরা বুঝতে পারলেন যে উচ্চতর মাত্রা যদি আদৌ থাকে, তাহলে তা একটা পরমাণুর চেয়ে ক্ষুদ্র হবে। গত শতাব্দীতে উচ্চতর মাত্রার ধারণায় নিয়ে কথা বলেছেন অধ্যাত্মবাদী ও গণিতবিদেরা। কিন্তু এতকাল তা উপহাস করে বাতিল করে দিয়েছেন পদার্থবিদেরা। কারণ, কোনো বস্তুকে কেউই কখনো কোনো উচ্চতর মাত্রায় ঢুকতে দেখেনি।

তত্ত্বটিকে উদ্ধার করতে পদার্থবিদেরা তাই প্রস্তাব করলেন যে উচ্চতর এসব মাত্রা এতই ছোট যে প্রকৃতিতে তাদের দেখা সম্ভব হবে না। আমাদের বিশ্ব চতুর্থমাত্রিক বিশ্ব। এর মানে হলো পঞ্চম মাত্রা একটা পরমাণুর চেয়েও খুদে কোনো বৃত্তের মধ্যে কুঁকড়ে আছে। একে পরীক্ষামূলকভাবে পর্যবেক্ষণ করা যায় না সে কারণেই।

ঠিক একই ধরনের সমস্যার মুখে পড়তে হয়েছিল স্ট্রিং থিওরিকেও। আমাদেরকেও এই অনাকাঙ্ক্ষিত উচ্চতর মাত্রাগুলোকে একটা খুদে বলের মধ্যে সংকুচিত করে রাখতে হয়েছে (এ প্রক্রিয়াকে বলা হয় কমপ্যাক্টিফিকেশন)। স্ট্রিং থিওরি অনুসারে, মহাবিশ্ব আসলে ১০ মাত্রার। সেখানে সবগুলো বল স্ট্রিংয়ের মাধ্যমে একীভূত হয়ে থাকে। তবে দশ-মাত্রিক হাইপারস্পেস অস্থিতিশীল। মহাবিস্ফোরণে দশটির মধ্যে ছয়টি এটা ক্ষুদ্র বলের মধ্যে কুঁকড়ে যেতে শুরু করে এবং বাইরের দিকে প্রসারিত হতে থাকে বাকি চারটি মাত্রা। অন্য মাত্রাগুলো আমরা দেখতে পারি না, তার কারণ হলো, সেগুলো একটা পরমাণুর চেয়েও অনেক ছোট। কাজেই তার ভেতরে কোনো কিছুই যেতে পারে না। (উদাহরণস্বরূপ, একটা গার্ডেন হোস আর একটা খড়কে দূর থেকে তাদের দৈর্ঘ্যের কারণে একমাত্রিক বস্তু বলে মনে হয়। কিন্তু ওগুলোকে খুব কাছ থেকে খেয়াল করলে, দেখা যাবে যে সেগুলো আসলে দ্বিমাত্রিক পৃষ্ঠতল বা সিলিন্ডার। কিন্তু দ্বিতীয় মাত্রাটি কুঁকড়ে থাকার কারণে সেটা দেখা যায় না।)

স্ট্রিং কেন

একটা ইউনিফায়েড ফিল্ড থিওরির আগের সব প্রচেষ্টা ব্যর্থ হলেও, একে একে সবগুলো চ্যালেঞ্জ মোকাবিলা করে টিকে গেছে স্ট্রিং থিওরি। আসলে এর কোনো প্রতিদ্বন্দ্বী নেই। দুটি কারণে স্ট্রিং থিওরি সফলতা পেয়েছে, যেখানে অন্য বেশ কিছু তত্ত্ব ব্যর্থ হয়েছে।

প্রথমত, একটা প্রসারিত বস্তুর (স্ট্রিং) ওপর ভিত্তি করে গড়ে ওঠার কারণে বিন্দু কণার সঙ্গে সংশ্লিষ্ট বেশ কিছু বিচ্যুতিগত সমস্যা এড়াতে পারে এই তত্ত্ব। নিউটন যেমন পর্যবেক্ষণ করেছিলেন, একটা বিন্দু কণার চারদিকে থাকা মহাকর্ষ বলের কাছাকাছি গেলে তা অসীম হয়ে যায়। (নিউটনের বিখ্যাত বিপরীত বর্গীয় সূত্রে মহাকর্ষ বল 1/r^2 হারে বাড়ে। তাই তার কাছাকাছি আমরা যেতে থাকলে তা অসীমের দিকে যেতে থাকে। অর্থাৎ যখন r শূন্য হয়ে যায়, তখন মহাকর্ষ বল বাড়ে 1/0, যার মান অসীম।)

এমনকি কোয়ান্টাম তত্ত্বেও আমরা যখন কোনো কোয়ান্টাম বিন্দু কণার কাছাকাছি যাই, তখন বলটি অসীম হয়। এগুলোসহ বিব্রতকর অন্য বিচ্যুতিগুলো মেরামত করতে কয়েক দশক ধরে ধারাবাহিকভাবে এই রহস্যময় নিয়মগুলো উন্মোচন করেন ফাইনম্যান এবং আরও অনেকে। কিন্তু মহাকর্ষের একটা কোয়ান্টাম তত্ত্বে ক্ষেত্রের সবগুলো অসীম দূর করতে ফাইনম্যানের আবিষ্কৃত ব্যাগভর্তি কৌশলও যথেষ্ট ছিল না। সমস্যাটি হলো, বিন্দু কণাগুলো অসীমভাবে ক্ষুদ্র। তার মানে, তাদের বলগুলো ও শক্তি সম্ভাবনীয়ভাবে অসীম।

কিন্তু সতর্কভাবে স্ট্রিং থিওরি বিশ্লেষণ করে দেখা যায়, দুটি কৌশল এসব বিব্রতকর বিচ্যুতি দূর করতে পারে। প্রথম কৌশলটির কারণ হলো স্ট্রিংয়ের টপোলজি। আর দ্বিতীয়টির কারণ হলো তার প্রতিসাম্যতা। একে বলা হয় সুপারসিমেট্রি বা অতিপ্রতিসাম্যতা।

বিন্দু কণার টপোলজি থেকে স্ট্রিং থিওরির টপোলজি একেবারেই আলাদা। সে কারণে এর বিচ্যুতিতেও পার্থক্য থাকে। (মোটা দাগে বললে, স্ট্রিংয়ের একটা সসীম দৈর্ঘ্য থাকার কারণে, স্ট্রিংয়ের কাছে গেলে এই বলগুলো আর অসীমের দিকে যেতে পারে না। স্ট্রিংয়ের কাছে গেলে বলগুলো মাত্র 1/L^2 হারে বাড়ে। এখানে L হলো স্ট্রিংয়ের দৈর্ঘ্য, যা প্ল্যাঙ্ক দৈর্ঘ্য ১০^-৩৩ সেন্টিমিটারের সমান। দৈর্ঘ্য L বিচ্যুতিগুলো দূর করে।) একটা স্ট্রিং বিন্দু কণা না হয়ে তার একটা নির্দিষ্ট আকার থাকার কারণে দেখানো যায় যে এই বিচ্যুতিগুলোকে দূর করে দেয় স্ট্রিং। এর ফলে সব ভৌত পরিমাণ সসীম হয়ে যায়।

এ কারণে একে সুস্পষ্ট বলে মনে হলেও, স্ট্রিং থিওরির বিচ্যুতিগুলো দূর হয়ে সসীম হয়। এ ঘটনার নির্দিষ্ট গাণিতিক প্রকাশ বেশ কঠিন। আবার একে প্রকাশ করা হয় উপবৃত্তাকার মডিউলার ফাংশনের মাধ্যমে। এই ফাংশন গণিতের অন্যতম অদ্ভুত ফাংশন। এর ইতিহাস এতই চমকপ্রদ যে হলিউডের এক চলচ্চিত্রে মূল ভূমিকায় দেখা গিয়েছিল একে। গুড উইল হান্টিং নামের মুভিটির গল্প কেমব্রিজ বিশ্ববিদ্যালয়ের কাছের অমার্জিত শ্রমজীবী এক ছেলের গল্প। এই চরিত্রে অভিনয় করেছেন ম্যাট ডেমন। ছেলেটির মধ্যে একসময় বিস্ময়কর গাণিতিক দক্ষতা দেখা যায়। যন্ত্রণাদায়ক প্রতিবেশীদের সঙ্গে লড়াইয়ে না নেমে এমআইটির দারোয়ান হিসেবে কাজে যোগ দেয় ছেলেটি। এমআইটির অধ্যাপকেরা হতবাক হয়ে দেখেন, রাস্তার এই ছেলেটি আসলে বিস্ময়কর এক গণিতপ্রতিভা। জটিল সব গাণিতিক সমস্যা খুব সহজে সমাধান করতে পারে ছেলেটা। আরও দেখা গেল, ছেলেটি উচ্চতর গণিত শিখেছে নিজে নিজেই। অধ্যাপকদের মধ্যে একজন উপলব্ধি করেন, এই ছেলেটিই হতে যাচ্ছে ‘পরবর্তী রামানুজন’।

গুড উইল হান্টিং মুভিটি আসলে শ্রীনিবাস রামানুজনের জীবনের ছায়া অবলম্বনে বানানো হয়েছিল। তিনি ছিলেন বিশ শতকের অন্যতম সেরা গণিতপ্রতিভা। ভারতের মাদ্রাজের কাছের এক শহরে গত শতকের শেষ দিকে দারিদ্র্য আর বিচ্ছিন্নতার মধ্য দিয়ে বেড়ে ওঠেন রামানুজন। বিচ্ছিন্নতার মধ্যে বাস করতে করতে উনিশ শতকের ইউরোপের গণিতবিদদের আবিষ্কৃত অনেক কিছুই তাঁকে শিখতে হয়েছিল নিজে নিজে। তাঁর ক্যারিয়ার অনেকটা সুপারনোভার মতো। কারণ, তাঁর গাণিতিক মেধা অতি সংক্ষিপ্ত সময়ে আকাশ আলোকিত করেছিল। দুর্ভাগ্যজনকভাবে, যক্ষ্মা রোগে ভুগে ১৯২০ সালে মাত্র ৩৭ বছর বয়সে মারা যান রামানুজন। গুড উইল হান্টিং মুভির ম্যাট ডেমনের মতো গাণিতিক সমীকরণের স্বপ্ন দেখতেন তিনিও। এর মধ্যে একটা হলো উপবৃত্তাকার মডিউলার ফাংশন। এ ফাংশনটি অদ্ভুত হলেও এর চমৎকার কিছু গাণিতিক বৈশিষ্ট্য রয়েছে। তবে সেগুলো আমাদের চেনাজানা মাত্রিক জগতে নয়, বরং ২৪ মাত্রায়। রামানুজনের মৃত্যুর পর তাঁর হারিয়ে যাওয়া নোটবুকের সন্ধান পাওয়া যায়। গণিতবিদেরা এখনো এই নোটবুকের অর্থ উদ্ধারের চেষ্টা করছেন। রামানুজনের কাজগুলোর দিকে খেয়াল করলে আমরা দেখতে পাব, একে আট মাত্রায় সাধারণীকরণও করা যায়, যা সরাসরি স্ট্রিং থিওরিতে প্রয়োগযোগ্য। একটা ভৌত তত্ত্ব কাঠামোবদ্ধ করতে এর সঙ্গে দুটো অতিরিক্ত মাত্রা যোগ করেন পদার্থবিদেরা। (যেমন আলোর দুটি ভৌত পোলারাইজেশন আছে। এ ঘটনাটা ব্যবহার করে তৈরি করা হয় পোলারাইজড সানগ্লাস। এটা বাঁ-ডানে বা ওপর-নিচে কম্পিত হতে পারে। কিন্তু ম্যাক্সওয়েলের সমীকরণে আলোর গাণিতিক বিবৃতি চারটি উপাদান দেয়। এই চারটি কম্পনের মধ্যে দুটি আসলে অতিরিক্ত বা অনাবশ্যক।) রামানুজনের ফাংশনে আমরা যখন আরও দুটি মাত্রা যোগ করি, তখন গণিতের ম্যাজিক নম্বরটি হয়ে যায় ১০ এবং ২৬। সেটা নিখুঁতভাবে স্ট্রিং থিওরির ম্যাজিক নম্বরের সঙ্গে মিলে যায়। কাজেই এক অর্থে বলা যায়, রামানুজন প্রথম বিশ্বযুদ্ধের আগেই স্ট্রিং থিওরি নিয়ে কাজ করেছেন!

এই উপবৃত্তাকার মডিউলার ফাংশনের (এলিপটিকেল মডিউলার ফাংশন বিস্ময়কর বৈশিষ্ট্যগুলো ব্যাখ্যা করে, এই তত্ত্বটি কেন অবশ্যই দশ মাত্রায় বিরাজ করতে হবে। কেবল এই নির্দিষ্টসংখ্যক মাত্রাতে বেশির ভাগ বিচ্যুতি ঘটে যেন সেটা কোনো ম্যাজিক। অথচ এই বিচ্যুতির উৎপাতে স্রেফ হারিয়ে গেছে অন্য তত্ত্বগুলো। তবে স্ট্রিংগুলোর টপোলজি নিজে থেকে সব বিচ্যুতি দূর করতে যথেষ্ট শক্তিশালী নয়। তত্ত্বের বাকি বিচ্যুতিগুলো স্ট্রিং তত্ত্বের দ্বিতীয় বৈশিষ্ট্য দূরে করে দেয়। সেটা বৈশিষ্ট্যটা হলো তার সিমেট্রি বা প্রতিসাম্যতা।

সুপারসিমেস্ট্রি বা অতিপ্রতিসাম্য

স্ট্রিংয়ে কিছু বৃহত্তর সিমেট্রি থাকে। চতুর্থ অধ্যায়ে স্ফীতি ও স্ট্যান্ডার্ড মডেলের আলোচনায় দেখা গেছে, প্রতিসাম্যতা থেকে আমরা সুন্দর একটি উপায় পাই। এর মধ্যে অতিপারমাণবিক কণাগুলোকে সন্তোষজনক ও অভিজাত একটা সজ্জায় সাজানো যায়। তিন ধরনের কোয়ার্ককে সিমেট্রি SU(3) অনুযায়ী সাজানো যায়। সেখানে নিজেদের মধ্যে আন্তবিনিময়ে অংশ নেয় তিনটি কোয়ার্ক। GUT তত্ত্বে বিশ্বাস করা হয়, পাঁচ ধরনের কোয়ার্ক ও লেপটন হয়তো সিমেট্রি SU(5) অনুযায়ী সাজানো সম্ভব।

স্ট্রিং থিওরিতে, এসব সিমেট্রি তত্ত্বের ভেতরের অবশিষ্ট বিচ্যুতি ও অস্বাভাবিকতা (অ্যানোমালি) বাতিল করে। প্রতিসাম্যতা আমাদের নিয়ন্ত্রণে থাকা সবচেয়ে সুন্দর ও শক্তিশালী হাতিয়ারগুলোর মধ্যে অন্যতম। তাই অনেকে হয়তো প্রত্যাশা করতে পারে যে মহাবিশ্বের এ তত্ত্বটি অবশ্যই বিজ্ঞানের জানা সবচেয়ে অভিজাত ও শক্তিশালী প্রতিসাম্যতা ধারণ করবে। যৌক্তিক পছন্দটি হলো, এমন একটা প্রতিসাম্যতা, যা শুধু কোয়ার্কই নয়, বরং প্রকৃতিতে দেখতে পাওয়া সবগুলো কণার আন্তবিনিময়ে অংশ নেয়। অর্থাৎ যদি সব অতিপারমাণবিক কণাকে তাদের মধ্যে রদবদল করে, তাহলে সমীকরণগুলো আগের মতো একই থাকবে। এটি নির্দিষ্টভাবে সুপারস্টিংয়ের সিমেট্রি বা প্রতিসাম্যতার ব্যাখ্যা করে, যাকে বলা হয় সুপারসিমেট্রি বা অতিপ্রতিসাম্যতা। এটিই একমাত্র প্রতিসাম্য, যা পদার্থবিজ্ঞানের জানা সব অতিপারমাণবিক কণার মধ্যে আন্তবিনিময় করে। এই প্রতিসাম্যতা মহাবিশ্বের সবগুলো কণাকে একটামাত্র অভিজাত, একীভূত করে সাজাতে পারে। সেজন্য এটা প্রতিসাম্যতার একটা আদর্শ প্রার্থী।

,

মহাবিশ্বের বল ও কণাগুলোর দিকে তাকালে স্পিনের ওপর ভিত্তি করে তাদের দুটি ভাগে বিভক্ত করা যায়। যথা ফার্মিয়ন ও বোসন। কণাগুলো অনেকটা খুদে লাটিমের মতো আচরণ করে, যারা বিভিন্ন হারে স্পিন করে বা ঘুরতে পারে। যেমন আলোর কণা ফোটন বিদ্যুৎ-চুম্বকীয় বলের বাহক, যার স্পিন ১। দুর্বল ও শক্তিশালী নিউক্লিয়ার বলের বাহক ডব্লিউ-বোসন ও গ্লুয়ন। এদের স্পিনও ১। মহাকর্ষের কণা গ্র্যাভিটনের স্পিন ২। পূর্ণ সংখ্যার এসব স্পিনকে বলা হয় বোসন। একইভাবে পদার্থ কণাকে এমন অতিপারমাণবিক কণা দিয়ে ব্যাখ্যা করা হয়, যাদের স্পিন অর্ধপূর্ণ সংখ্যা—১/২, ৩/২, ৫/২ ইত্যাদি। (অর্ধপূর্ণ সংখ্যার স্পিনসম্পন্ন কণাদের বলে ফার্মিয়ন। এর মধ্যে আছে ইলেকট্রন, নিউট্রিনো আর কোয়ার্ক।) কাজেই সুপারসিমেট্রি বেশ অভিজাতভাবে বোসন আর ফার্মিয়নের মধ্যে, বল ও পদার্থের মধ্যে দ্বৈততার প্রতিনিধিত্ব করে।

সুপারসিমেট্রি তত্ত্বে সবগুলো অতিপারমাণবিক কণার একটা করে পার্টনার বা সঙ্গী থাকে। মানে, প্রতিটি ফার্মিয়ন একটা বোসনের সঙ্গে জোড় বাঁধে। অবশ্য আমরা সব সুপারসিমেট্রিক পার্টনারগুলোকে প্রকৃতিতে কখনো দেখিনি। তারপরও পদার্থবিদেরা ইলেকট্রনের সঙ্গীর নাম দিয়েছেন সিলেকট্রন, যার স্পিন ০। (ইলেকট্রনের সঙ্গে একটা s বা এস যোগ করে কণাটির সুপারপার্টনারের নামকরণ করা হয়েছে।) দুর্বল মিথস্ক্রিয়ার অন্তর্ভুক্ত লেপটন কণার সুপারপার্টনারকে বলা হয় এসলেপ্টন বা স্লেপ্টন। একইভাবে কোয়ার্কের ০ স্পিনসম্পন্ন সঙ্গীর নাম এসকোয়ার্ক। সাধারণভাবে আমাদের জানা কণাগুলোর (কোয়ার্ক, লেপটন, গ্র্যাভিটন, ফোটন ও অন্যান্য) সঙ্গীদের বলা হয় এসপার্টিকেল বা সুপারপার্টিকেট। অ্যাটম স্ম্যাশারে এখনো কোনো এসপার্টিকেল খুঁজে পাওয়া যায়নি (এর কারণ হতে পারে, আমাদের যন্ত্রগুলো হয়তো তাদের তৈরি করার মতো যথেষ্ট শক্তিশালী নয়)।

অতিপারমাণবিক কণা হয় ফার্মিয়ন, নয়তো বোসন। তাই একটা সুপারসিমেট্রিক তত্ত্বের সব জানা অতিপারমাণবিক কণাকে একটা সরল প্রতিসাম্যতায় একীভূত করার সম্ভাবনা থাকে। আমাদের কাছে এখন এমন এক বৃহৎ প্রতিসাম্যতা আছে, যার মধ্যে গোটা মহাবিশ্বকে অন্তর্ভুক্ত করা যায়।

একটা তুষারকণার কথা ভাবুন। তুষারকণার ছয়টি তীক্ষ্ণ শীর্ষের প্রতিটিকে একেকটা অতিপারমাণবিক কণার প্রতীক ধরা যাক। প্রতিটি শীর্ষ একটা বোসন হবে এবং তাকে যা অনুসরণ করবে সেটি হবে ফার্মিয়ন। সুপার তুষারকণার সৌন্দর্য হলো, একে ঘোরানো হলেও তার চেহারা একই থাকবে। এভাবে সুপার তুষারকণা সবগুলো কণা ও তাদের সুপারপার্টনারকে একীভূত করতে পারে। সুতরাং হাইপোথেটিক্যাল ইউনিফায়েড ফিল্ড থিওরি সূত্রবদ্ধ করার চেষ্টা চালালে স্বাভাবিকভাবে সেখানে প্রার্থী হয়ে উঠবে এই সুপার তুষারকণা।

অতিপ্রতিসাম্যতা অবশিষ্ট অসীমগুলোকে দূর করতে সহায়তা করে। এই অসীমগুলোই অন্য তত্ত্বগুলোর জন্য একসময় মারাত্মক হয়ে উঠেছিল। আগে বলেছি, বেশির ভাগ বিচ্যুতিই দূর হয়ে স্ট্রিংয়ের টপোলজির কারণে। অর্থাৎ স্ট্রিংয়ের একটা সসীম দৈর্ঘ্য থাকার কারণে বলগুলো অসীমের দিকে যেতে পারে না। বাকি বিচ্যুতিগুলো পরীক্ষার সময় দেখা যায়, বোসন ও ফার্মিয়নের মিথস্ক্রিয়ার কারণে তারা দুই ধরনের। তবে এই দুই ধরন সব সময় বিপরীত চিহ্ন নিয়ে ঘটে। তাতে বোসনের অবদান নিখুঁতভাবে ফার্মিয়নের অবদানকে বাতিল করে দিতে পারে। অন্য কথায়, ফার্মিয়নিক ও বোসনিক অবদান সব সময় বিপরীত চিহ্নের হয়, যা তত্ত্বের বাকি অসীমগুলোকে বাতিল করে। কাজেই অতিপ্রতিসাম্যতা একটা সুন্দর সজ্জার চেয়েও বেশি কিছু। এটি শুধু নান্দনিকভাবে প্রতিসাম্যতাকে সন্তুষ্ট করে না (কারণ, এটা প্রকৃতির সব কণাকে একীভূত করে), বরং স্টিং থিওরির বিচ্যুতিগুলোকেও অনিবার্যভাবে বাতিল করে।

মসৃণ ও গতিময় সেই রকেট ডিজাইনের কথা আরেকবার স্মরণ করা যাক। সেখানে পাখার কম্পন হয়তো একসময় বেড়ে পাখাগুলোকে ভেঙে ফেলতে পারত। এর একটি সমাধান হলো, পাখাগুলো ডিজাইন করতে প্রতিসাম্যতার শক্তি ব্যবহার করা। তাতে একটি পাখার কম্পন আরেকটি পাখার কম্পন বাতিল করে দিতে পারে। একটি পাখার কম্পন যদি ঘড়ির কাঁটার দিকে হয়, আরেকটি পাখার কম্পন যদি ঘড়ির কাঁটার বিপরীত দিকে হয়, তাহলে সেগুলো বাতিল করবে পরস্পরকে। কাজেই রকেটের এই প্রতিসাম্যতা শুধু কৃত্রিম নয়, বরং শৈল্পিক যন্ত্র, যা পাখাগুলোর প্রবল চাপকে বাতিল ও ভারসাম্যে রাখে। একইভাবে সুপারসিমেট্রিও বোসনিক আর ফার্মিওনিক অংশগুলো পরস্পরকে বাতিল করার মাধ্যমে বিচ্যুতিগুলো দূর হয়।

(সুপারসিমেট্রি আবার একগুচ্ছ বড় ধরনের টেকনিক্যাল সমস্যারও সমাধান করতে পারে। সেগুলো GUT তত্ত্বের জন্য খুবই মারাত্মক। GUT তত্ত্বে জটিল গাণিতিক অসংগতিগুলো দূর করার জন্য সুপারসিমেট্রি দরকার। )

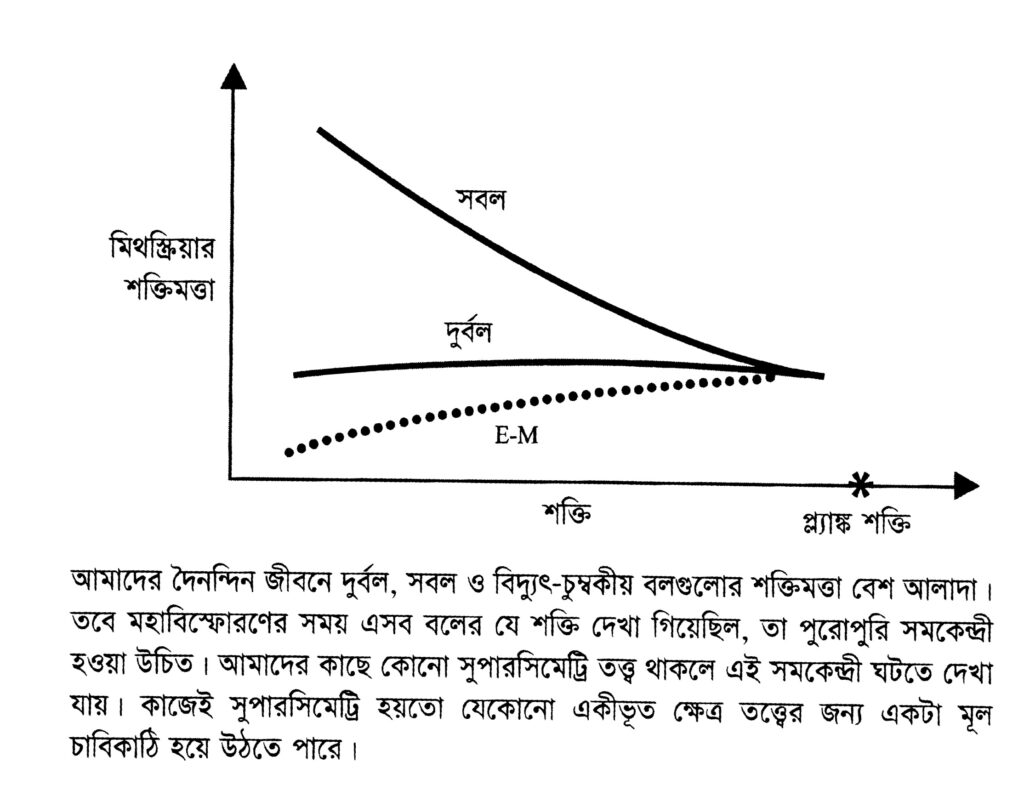
সুপারসিমেট্রি একটা শক্তিশালী আইডিয়ার প্রতীক হলেও, বর্তমানে একে সমর্থনের মতো কোনো পরীক্ষামূলক প্রমাণ নেই। কারণ, হয়তো আমাদের পরিচিত ইলেকট্রন ও প্রোটনের সুপার পার্টনারগুলো এত ভারী যে তাদের বর্তমানের প্রচলিত পার্টিকেল অ্যাকসিলারেটরে উৎপাদন করা সম্ভব নয়। তবে বিশ্বাস জাগানোর মতো একটা প্রমাণও আছে, সেটা সুপারসিমেট্রির দিকে ইঙ্গিত করে। আমরা এখন জানি, তিনটি কোয়ান্টাম বলের শক্তিমত্তা বেশ আলাদা। আসলে নিম্ন শক্তিতে দুর্বল বলের চেয়ে শক্তিশালী বল ৩০ গুণ বেশি শক্তিশালী এবং বিদ্যুৎ-চুম্বকীয় বলের চেয়ে ১০০ গুণ বেশি শক্তিশালী। তবে সব সময় তা একই রকম ছিল না। আমাদের ধারণা, মহাবিস্ফোরণের ঠিক পরপরই এই বলগুলোর শক্তিমত্তা সমান সমান ছিল। পেছনের দিকে হিসাব করে এই তিনটি বলের শক্তিমত্তা সময়ের শুরুতে কেমন হতে পারে, তা গণনা করেছেন পদার্থবিদেরা। স্ট্যান্ডার্ড মডেল বিশ্লেষণ করে পদার্থবিদেরা দেখেছেন, বল তিনটি মহাবিস্ফোরণের সময় শক্তিমত্তায় সমকেন্দ্রী ছিল, কিন্তু নিখুঁতভাবে সমান ছিল না। তবে একটা সুপারসিমেট্রি যোগ করলে বল তিনটি সঠিকভাবে খাপ খায়। আবার সেগুলো শক্তিমত্তাতেও সমান হয়ে যায়, ঠিক যেমন একটা ইউনিফায়েড ফিল্ড থিওরি প্রস্তাব করে। অবশ্যই এটা সরাসরি সুপারসিমেট্রির কোনো প্রমাণ নয়। তা না হলেও অন্তত এটা দেখায়, সুপারসিমেট্রি আমাদের জানা পদার্থবিজ্ঞানের সঙ্গে বেশ মানানসই।

স্ট্যান্ডার্ড মডেলের উদ্ভব

সুপারস্ট্রিংয়ের কোনো মানানসই প্যারামিটার না থাকলেও স্ট্রিং থিওরি এমন এক সমাধানের প্রস্তাব করে, যা বিস্ময়করভাবে স্ট্যান্ডার্ড মডেলের সঙ্গে প্রায় মিলে যায়। স্ট্যান্ডার্ড মডেলের মধ্যে আছে বিচিত্র ধরনের অদ্ভুত অতিপারমাণবিক কণা এবং ১৯টি মুক্ত প্যারামিটার (যেমন কণাদের ভর ও কাপলিংয়ের শক্তিমত্তা)। আবার স্ট্যান্ডার্ড মডেলে সবগুলো কোয়ার্ক ও লেপটনের তিনটি একই রকম ও বাড়তি প্রতিলিপি আছে। সেগুলো দেখতে অপ্রয়োজনীয় বলে মনে হয়। ভাগ্যক্রমে, স্ট্যান্ডার্ড মডেলের অনেকগুলো গুণগত ধর্ম অনায়াসে বের করে আনতে পারে স্ট্রিং থিওরি। অনেকটা শূন্য থেকে কিছু পাওয়ার মতো। ১৯৮৪ সালে টেক্সাস বিশ্ববিদ্যালয়ের ফিলিপ ক্যানডিলাস, সান্তা বারবারায় ক্যালিফোর্নিয়া বিশ্ববিদ্যালয়ের গ্যারি হোরোউইজ ও অ্যাড্রিউ স্ট্রোমিনজার এবং এডওয়ার্ড উইটেন প্রমাণ করেন, স্ট্রিং থিওরির ১০টির মধ্যে ৬টি মাত্রা যদি গুটিয়ে থাকে তারপরও সুপারসিমেট্রি সংরক্ষিত থাকে বাকি চারটি মাত্রায়। এই খুদে ছয় মাত্রিক বিশ্বকে ব্যাখ্যা করা যায় কালাবি-ইয়াউ ম্যানিফোল্ড দিয়ে। কালাবি-ইয়াউ স্থানের কিছু সরল বাছাইয়ের মাধ্যমে তাঁরা দেখান, স্ট্রিংয়ের প্রতিসাম্যতা ভেঙে গিয়ে তা লক্ষণীয়ভাবে স্ট্যান্ডার্ড মডেলের একটা তত্ত্বের মতো দাঁড়াতে পারে।

এইভাবে স্ট্যান্ডার্ড মডেলের কেন তিনটি বাড়তি প্রজন্ম থাকে, তার সরল উত্তরও দিতে পারে তার স্ট্রিং থিওরি। স্ট্রিং থিওরিতে কোয়ার্ক মডেলের প্রজন্ম সংখ্যা বা প্রাচুর্য কালাবি-ইয়াউ ম্যানিফোল্ডের ‘ছিদ্রের’ সংখ্যার সঙ্গে সম্পর্কিত। (যেমন একটা ডোনাট, একটা টিউবের ভেতরের অংশ এবং একটা কফি কাপ—সবগুলোর পৃষ্ঠতলে একটা ছিদ্র বা গর্ত থাকে। চোখের চশমায় থাকে দুটি গর্ত। আর কালাবি-ইয়াউ পৃষ্ঠতলে অনেকগুলো ছিদ্র বা গর্ত থাকতে পারে।) কাজেই সরলভাবে নির্দিষ্টসংখ্যক গর্তসম্পন্ন কালাবি-ইয়াউ ম্যানিফোল্ড পছন্দ করে আমরা বাড়তি কোয়ার্কের বিভিন্ন প্রজন্মের একটা স্ট্যান্ডার্ড মডেল গঠন করতে পারি। (আমরা কখনো কালাবি-ইয়াউ স্পেস দেখতে পাই না। কারণ, এটা খুব ছোট। আবার এই স্পেসে যে ডোনাটের মতো গর্ত থাকে, সেটাও আমরা কখনো দেখতে পাই না।) বেশ কয়েক বছর ধরে, সম্ভাব্য সব কালাবি-ইয়াউ স্থান তালিকাভুক্ত করার আপ্রাণ চেষ্টা করছেন পদার্থবিদেরা। কারণ, তাঁরা বুঝতে পেরেছেন, এই ছয়মাত্রিক স্থানের টপোলজি আমাদের চারমাত্রিক মহাবিশ্বের কোয়ার্ক ও লেপটন নির্ধারণ করে।

এম-থিওরি

স্ট্রিং থিওরি ঘিরে ১৯৮৪ সালে যে উত্তেজনার সৃষ্টি হয়েছিল, তা তো চিরকাল স্থায়ী হতে পারে না। ১৯৯০ দশকের মাঝামাঝি সুপারস্ট্রিংয়ের শোভাযাত্রার বাদকদল ধীরে ধীরে তাদের শক্তি হারাতে থাকে পদার্থবিদদের কাছে। তত্ত্ব থেকে উঠে আসা জটিল সমস্যাগুলোর পেছনে চাপা পড়তে থাকে। সেই সঙ্গে তাদের সামনে উঠে আসতে থাকে সহজ সমস্যাগুলো। এর মধ্যে একটা সমস্যা ছিল, স্ট্রিং সমীকরণের কোটি কোটি সমাধান আবিষ্কৃত হওয়া। স্থান- কালের কুঁকড়ে যাওয়াকে বিভিন্নভাবে দেখিয়ে স্ট্রিংয়ের সমাধানগুলো শুধু চার মাত্রায় নয়, বরং যেকোনো মাত্রা লেখা সম্ভব হয়েছিল। স্ট্রিংয়ের কয়েক কোটি সমাধানের প্রতিটিই গাণিতিকভাবে স্বনির্ভর মহাবিশ্বের সঙ্গে সম্পর্কিত।

পদার্থবিদেরা হঠাৎ করে স্ট্রিংয়ের এসব একগাদা সমাধানের তলায় ডুবে যেতে লাগলেন। বিশেষ করে এর মধ্যে অনেকগুলোকে আমাদের মহাবিশ্বের সঙ্গে বেশ মিল আছে বলে দেখা গেল। কালাবি-ইয়াউ স্থানের একটা উপযুক্ত পছন্দের মাধ্যমে সেটা তুলনামূলকভাবে সহজেই স্ট্যান্ডার্ড মডেলের অনেকগুলো বৈশিষ্ট্য দেখাতে পারে (স্ট্যান্ডার্ড মডেলের অদ্ভুত কোয়ার্ক ও লেপটনের গুচ্ছসহ, এমনকি তার বাড়তি প্রতিলিপিগুলোসহ)। তবে স্ট্যাডার্ড মডেলের ১৯টি প্যারামিটারের নির্দিষ্ট মানসহ এবং তিনটি বাড়তি প্রজন্মসহ একটা নিখুঁত স্ট্যান্ডার্ড মডেল খুঁজে পাওয়া খুব কঠিন (এমনকি সেটা এখনো অনেক বড় চ্যালেঞ্জ)। (বিস্ময়করসংখ্যক স্ট্রিংয়ের সমাধানগুলো স্বাগত জানান পদার্থবিদেরা। বিশেষ করে যারা মাল্টিভার্স আইডিয়ায় বিশ্বাস রাখেন। কারণ, প্রতিটি সমাধান সম্পূর্ণ স্বনির্ভর প্যারালাল মহাবিশ্বের প্রতিনিধিত্ব করে। কিন্তু বিপুলসংখ্যক মহাবিশ্বের জঙ্গলের মধ্যে সঠিকভাবে আমাদের নিজেদের মহাবিশ্ব খুঁজে পাওয়া বেশ কঠিন। সেটা পদার্থবিদদের জন্য বড্ড পীড়াদায়ক ছিল। )

এটা এত কঠিন হওয়ার একটা কারণ হলো, শেষ পর্যন্ত সুপারসিমেট্রি অবশ্যই ভেঙে ফেলতে হবে। কারণ, আমাদের নিম্ন-শক্তির বিশ্বে কোনো সুপারসিমেট্রি দেখা যায় না। যেমন প্রকৃতিতে সিলেকট্রন বা ইলেকট্রনের সুপারপার্টনার দেখা যায় না। সুপারসিমেট্রি যদি না ভেঙে যেত বা অবিচ্ছিন্ন থেকে যেত, তাহলে প্রতিটি কণার ভর তার সুপারপার্টিকেলের সমান হওয়ার কথা। সুপারসিমেট্রি ভেঙে যায় বলে মনে করেন পদার্থবিদেরা। ফলে সুপারপার্টিকেল বা অতিকণার ভর অনেক বড় হয়। আর তা আমাদের বর্তমানের প্রচলিত পার্টিকেল অ্যাকসিলারেটরের আওতার বাইরে। কিন্তু সুপারসিমেট্রি কেন ভেঙে গেল তার বিশ্বাসযোগ্য কোনো কৌশল এখনো পাওয়া যায়নি।

সান্তা বারবারায় কেভিল ইনস্টিটিউট ফর থিওরিটিক্যাল ফিজিকসের ডেভিড গ্রস মন্তব্য করেছেন, তিনটি স্থানিক মাত্রায় স্ট্রিং থিওরির কোটি কোটি সমাধান রয়েছে। সেগুলো বেশ বিব্রতকর। কারণ, তাদের মধ্য থেকে বেছে নেওয়ার ভালো কোনো উপায় নেই।

এ ছাড়া এতে আরও কিছু বিরক্তিকর প্রশ্নও আছে। এগুলোর মধ্যে সবচেয়ে বিব্রতকরটি হলো মোট পাঁচটি স্বনির্ভর স্ট্রিং থিওরি আছে। আমাদের মহাবিশ্ব পাঁচটি আলাদা একীভূত ক্ষেত্র তত্ত্ব সহ্য করতে পারে—তা ভাবাও কঠিন। আইনস্টাইন বিশ্বাস করতেন, মহাবিশ্ব সৃষ্টিতে ঈশ্বরের কোনো বিকল্প ছিল না। তাহলে ঈশ্বর কেন তাদের পাঁচটি তৈরি করবেন?

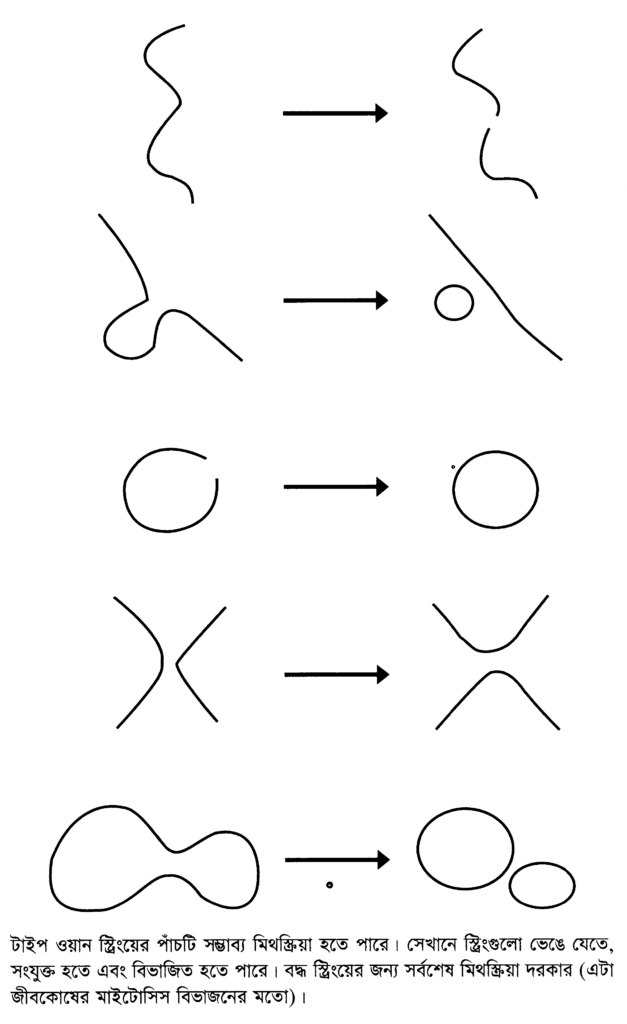
ভেনিজিয়ানো ফর্মুলার ওপর ভিত্তি করে গড়ে ওঠা আসল তত্ত্বটিকে বলা হয় টাইপ ওয়ান সুপারস্ট্রিং থিওরি। টাইপ ওয়ান তত্ত্বের ভিত্তি একই সঙ্গে উন্মুক্ত স্ট্রিং (যে স্ট্রিংয়ের দুই প্রান্ত থাকে) এবং বদ্ধ স্ট্রিং (বৃত্তাকার স্ট্রিং) তত্ত্বটিকে ১৯৭০-এর দশকের গোড়ার দিকে সবচেয়ে ভালোভাবে গবেষণা করা হয়েছে। (স্ট্রিং ক্ষেত্র তত্ত্ব ব্যবহার করে, কিক্কাওয়া এবং আমি টাইপ ওয়ান স্ট্রিংয়ের মিথস্ক্রিয়ার সম্পূর্ণ তালিকা তৈরি করেছি। আমরা দেখিয়েছি, টাইপ ওয়ান স্ট্রিংয়ের জন্য পাঁচটি মিথস্ক্রিয়া দরকার; বদ্ধ স্ট্রিংয়ের জন্য আমরা দেখিয়েছি, সেখানে শুধু একধরনের মিথস্ক্রিয়া দরকার।)

কিক্কায়া এবং আমি এটাও দেখিয়েছি, শুধু বদ্ধ স্ট্রিং দিয়েও পুরোপুরি স্বনির্ভর তত্ত্ব গঠন করা সম্ভব (লুপের মতো বদ্ধ স্ট্রিং)। বর্তমানে এদের বলা হয় টাইপ টু স্ট্রিং থিওরি। সেখানে স্ট্রিংগুলো একটা বৃত্তাকার স্ট্রিং চিমটি দেওয়ার মাধ্যমে দুটো ছোট স্ট্রিংয়ের সঙ্গে মিথস্ক্রিয়া করে (এর সঙ্গে জীবকোষের মাইটোসিস বিভাজনের মিল আছে)।

সবচেয়ে বাস্তবসম্মত স্ট্রিং থিওরিকে বলা হয় হেটেরোটিক স্ট্রিং। এটি সূত্রবদ্ধ করেছিল প্রিন্সটন গ্রুপ (এ দলে ছিলেন ডেভিড গ্রস, এমিল মার্টিনেক, রায়ান রোম এবং জেফরি হার্ভি)। হেটেরোটিক স্ট্রিং E(8) × E(8) বা O(32) নামের সিমেট্রি গ্রুপের সঙ্গে মানানসই, যা GUT তত্ত্বগুলোকে গ্রাস করার জন্য যথেষ্ট বড়। হেটেরোটিক স্ট্রিং পুরোপুরি বদ্ধ স্ট্রিংয়ের ওপর নির্ভরশীল। ১৯৮০ ও ১৯৯০-এর দশকে, বিজ্ঞানীরা যখন সুপারস্ট্রিংয়ের কথা উল্লেখ করেন, তখন তাঁরা নীরবে হেটেরোটিক স্ট্রিংয়ের কথাও উল্লেখ করেছিলেন। কারণ, স্ট্যান্ডার্ড মডেল ও GUT তত্ত্বগুলো বিশ্লেষণের জন্য এটা বেশ উন্নত যেমন E(8) × E(8) সিমেট্রি গ্রুপ E(8)-তে ভেঙে যেতে পারে। তারপর তা ভেঙে যেতে পারে E(6) সিমেট্রিতে। এটি স্ট্যান্ডার্ড মডেলের SU(3) × SU(2) × U(1) সিমেট্রিকে অন্তর্ভুক্ত করার জন্য বেশ বড় বলে দেখা যায়।

সুপারগ্র্যাভিটির রহস্য

পাঁচটি সুপারস্ট্রিং তত্ত্ব ছাড়াও এখানে নাছোড়বান্দার মতো আরেকটি প্রশ্ন আছে। সেটি স্ট্রিং থিওরি সমাধান করার উত্তেজনায় একদা ভুলে গিয়েছিল সবাই। ১৯৭৬ সালে নতুন একটা বিষয় আবিষ্কার করেন স্টোনি ব্রুকে নিউইয়র্ক স্টেট ইউনিভার্সিটিতে কর্মরত তিন পদার্থবিদ। তাঁরা হলেন পিটার ভ্যান নিউভেনহুইজেন, সার্জিও ফেরারা এবং ডেনিয়েল ফ্রিডম্যান। তাঁরা দেখলেন, আইনস্টাইনের মহাকর্ষের মৌলিক তত্ত্বটি সুপারসিমেট্রিক হতে পারে, যদি নতুন একটা ফিল্ড প্রবর্তন করা যায়। অর্থাৎ আসল মহাকর্ষ ক্ষেত্রের একটা সুপারপার্টনার (যাকে বলা হয় গ্র্যাভিটিনো। এর অর্থ, ছোট্ট গ্র্যাভিটন, যার স্পিন ৩/২)। নতুন এ তত্ত্বকে বলা হয় সুপারগ্র্যাভিটি বা অতিমহাকর্ষ। অসীম ক্রমের স্বর আর অনুরণনসহ সুপারগ্র্যাভিটির মাত্র দুটি কণা থাকে। ১৯৭৮ সালে ইউজিন ক্রেমার, জোয়েল শার্ক এবং ইকোল নরমেল সুপিরিয়রের বিজ্ঞানী বার্নাড জুলিয়া দেখান, বেশির ভাগ সাধারণ অতিমহাকর্ষকে ১১ মাত্রায় লেখা যায়। (আমরা যদি অতিমহাকর্ষ তত্ত্বকে ১২ বা ১৩ মাত্রায় লিখতে চাই, তাহলে গাণিতিক অসংগতি দেখা দিতে পারে।) ১৯৭০-এর দশকের শেষ দিকে এবং ১৯৮০-এর দশকের গোড়ার দিকে ভাবা হতো যে অতিমহাকর্ষ হয়তো কিংবদন্তিতুল্য একীভূত ক্ষেত্র

ত্ত্ব। তত্ত্বটি স্টিফেন হকিংকেও এ কথা বলতে অনুপ্রাণিত করেছিল তাত্ত্বিক পদার্থবিদ্যার সমাপ্তি’ দৃশ্যমান হচ্ছে। কেমব্রিজ বিশ্ববিদ্যালয়ের গণিতের লুকাসিয়ান চেয়ারে আসীন হওয়ার সময় উদ্বোধনী ভাষণে এ কথা বলেন তিনি। এই চেয়ারেই একসময় আসীন ছিলেন স্বয়ং আইজ্যাক নিউটন। কিন্তু আগের তত্ত্বগুলোও জটিল যেরকম সমস্যার মুখে পড়ে মৃত্যু ঘটেছিল, শিগগিরই একই সমস্যার মুখে পড়ে অতিমহাকর্ষও। তবে সাধারণ ক্ষেত্র তত্ত্বের তুলনায় এতে অসীমের পরিমাণ কম। তবু চূড়ান্ত বিশ্লেষণে অতিমহাকর্ষ সসীম হয় না এবং অস্বাভাবিকতার ধাঁধায় পড়ার সম্ভাবনা থাকে। অন্য সবগুলো ক্ষেত্র তত্ত্বের মতো এটাও বিজ্ঞানীদের মুখ রক্ষা করতে পারেনি (একমাত্র ব্যতিক্রম স্ট্রিং থিওরি)।

১১ মাত্রায় থাকতে পারা আরেকটি সুপারসিমেট্রি তত্ত্ব হলো সুপারমেমব্রেন থিওরি। স্ট্রিং মাত্র একমাত্রিক, যা তার দৈর্ঘ্য নির্ধারণ করে। কিন্তু তা হলেও সুপারমেমব্রেনের দুটি বা তারও বেশি মাত্রা থাকতে পারে। কারণ, এটি একটা পৃষ্ঠতলের প্রতিনিধিত্ব করে। লক্ষণীয় ব্যাপার হলো, এটি দেখায় যে দুই ধরনের মেমব্রেন (একটা দুই ব্রেন এবং পাঁচটি ব্রেন) ১১ মাত্রায় স্বনির্ভর।

তবে সুপারমেমব্রেনেরও কিছু সমস্যা আছে। এদের নিয়ে কাজ করা মারাত্মকভাবে কঠিন। আবার তাদের কোয়ান্টাম তত্ত্বগুলোও আসলে বিচ্যুত বা বিপথগামী। বেহালার তার এত সরল যে গ্রিক পিথাগোরিয়ানরা দুই হাজার বছর আগে তার হারমনির সূত্র নির্ণয় করতে পেরেছিল। অন্যদিকে মেমব্রেন এত জটিল ও কঠিন যে এখনো কারও কাছেই তাদের ওপর সংগীতভিত্তিক কোনো সন্তোষজনক তত্ত্ব নেই। আবার এটাও দেখা গেছে, এসব মেমব্রেন অস্থিতিশীল এবং ক্রমান্বয়ে ক্ষয় হয়ে বিন্দু কণায় পরিণত হয়।

কাজেই ১৯৯০ দশকের মাঝামাঝি এসে পদার্থবিদদের কাছে অনেকগুলো রহস্য ছিল। ১০ মাত্রায় পাঁচটি স্ট্রিং থিওরি আছে কেন? আর ১১ মাত্রায় সুপারগ্র্যাভিটি এবং সুপারমেমব্রেন নামের দুটি তত্ত্ব আছে কেন? সর্বোপরি তাদের সবগুলোই সুপারসিমেট্রি ধারণ করে।

এগারো মাত্রা

১৯৯৪ সালে হঠাৎ একটা বোমা ফাটল। আরেকটা বড় ধরনের ঘটনা পুরো দৃশ্যপট পাল্টে দিল আরেকবার। কেমব্রিজ বিশ্ববিদ্যালয়ের এডওয়ার্ড উইটেন এবং পল টাউনসেন্ড গাণিতিকভাবে দেখতে পান, দশ-মাত্রিক স্ট্রিং থিওরি আসলে একটা উচ্চতর, রহস্যময়, অজানা জায়গা থেকে আসা এগারো-মাত্রিক তত্ত্বের আসন্নতা। যেমন উইটেন দেখালেন, আমরা যদি মেমব্রেনের মতো কোনো তত্ত্ব এগারো মাত্রায় নিয়ে যাই এবং একটা মাত্রাকে কুঁকড়ে ছোট করে ফেলি, তাহলে সেটা দশমাত্রিক টাইপ টু স্ট্রিং থিওরিতে পরিণত হয়।

শিগগিরই আরও দেখা গেল, পাঁচটি স্ট্রিং থিওরির সবগুলো একই হিসেবে দেখানো যায়। অর্থাৎ একই রহস্যময় এগারো-মাত্রিক তত্ত্বের ভিন্ন ভিন্ন আসন্নতা। বিভিন্ন মেমব্রেন এগারো-মাত্রায় থাকতে পারার কারণে উইটেন নতুন এ তত্ত্বকে বললেন, এম-থিওরি। কিন্তু এটা শুধু পাঁচটি ভিন্ন ভিন্ন স্ট্রিং তত্ত্বগুলোকে একীভূতই করল না, সঙ্গে বোনাস হিসেবে ব্যাখ্যা করল অতিমহাকর্ষের রহস্যও।

আপনার হয়তো মনে আছে, অতিমহাকর্ষ হলো এগারো-মাত্রিক তত্ত্ব। এখানে মাত্র শূন্য ভরের দুটি কণা থাকে। সেগুলো হলো আইনস্টাইনের গ্র্যাভিটন, প্লাস তার সুপারসিমেট্রিক পার্টনার (যার নাম গ্র্যাভিটিনো)। তবে এম-থিওরিতে বিভিন্ন ভরের অসীমসংখ্যক কণা থাকে (যার সঙ্গে অসীম কম্পন সংশ্লিষ্ট, যা এগারো-মাত্রিক মেমব্রেনের কোনো কিছুতে তরঙ্গ সৃষ্টি করতে পারে)। কিন্তু এম-থিওরিও অতিমহাকর্ষের অস্তিত্বকে ব্যাখ্যা করতে পারে, যদি আমরা ধরে নিই যে এম-থিওরির একটা ক্ষুদ্র অংশ (শুধু ভরহীন কণা) হলো পুরোনো অতিমহাকর্ষ তত্ত্ব। অন্য কথায়, সুপারগ্র্যাভিটি বা অতিমহাকর্ষ তত্ত্ব হলো এম-থিওরির একটা ক্ষুদ্র সাবসেট। একইভাবে আমরা যদি এই রহস্যময় এগারো-মাত্রিক মেমব্রেনের মতো তত্ত্ব এবং কুঁকড়ে যাওয়া একটা মাত্রা গ্রহণ করি, তাহলে মেমব্রেনগুলো স্ট্রিংয়ে পরিণত হয়। আসলে এটা নিখুঁতভাবে টাইপ টু স্ট্রিং থিওরিতে পাল্টে যায়! উদাহরণ হিসেবে, আমরা যদি এগারো-মাত্রার কোনো গোলকের দিকে তাকাই, তারপর কুঁকড়ে যাওয়া একটা মাত্রার দিকে তাকাই, তাহলে গোলকটি ভেঙে যাবে এবং তার মেরুগুলো একটা বদ্ধ স্ট্রিংয়ে পরিণত হবে। আমরা দেখতে পাই, এগারোতম মাত্রাটিকে একটা ছোট্ট বৃত্তের মধ্যে কুঁকড়ে ফেলা হলে স্ট্রিং থিওরিকে এগারো মাত্রায় এক মেমব্রেনের টুকরো হিসেবে দেখা যায়।

কাজেই দশ-মাত্রা ও এগারো-মাত্রার পদার্থবিজ্ঞানের সবগুলোকে একটামাত্র তত্ত্বে একীভূত করার একটা চমৎকার ও সরল পথ খুঁজে পাওয়া যায়! এটা ছিল একটা ধারণাগত কৌশল।

এই বোমা ফাটানোর মতো আবিষ্কারের কারণে যে তীব্র অভিঘাতের জন্ম দিয়েছিল, সেই স্মৃতি আমার মনে এখনো দাগ কেটে আছে। তখন কেমব্ৰিজ বিশ্ববিদ্যালয়ে এক বক্তৃতা দিচ্ছিলাম আমি। বেশ উদারতা দেখিয়ে পল টাউনসেন্ড দর্শকদের সঙ্গে আমাকে পরিচয় করিয়ে দিলেন। কিন্তু আমার বক্তৃতার আগে, নতুন এ ফলাফল প্রবল উত্তেজিত হয়ে ব্যাখ্যা করলেন তিনি। জানালেন, এগারোতম মাত্রায় বিভিন্ন স্ট্রিং থিওরিকে একটামাত্র তত্ত্বে একীভূত করা যায়। আমার বক্তৃতার শিরোনাম উল্লেখ করলেন দশম মাত্রা। আমি কথা শুরু করার আগে আমাকে বললেন, এটা যদি সফলভাবে প্রমাণ করা যায়, তাহলে আমার বক্তৃতার শিরোনাম অচল হয়ে যাবে।

আমি মনে মনে ভাবলাম, ‘আহ।’ হয় তিনি পাগল হয়ে গেছেন, নয়তো পদার্থবিজ্ঞান সম্প্রদায় পুরোপুরি উল্টো দিকে যাচ্ছে।

নিজের কানে শুনেও কথাটা বিশ্বাস করতে পারছিলাম না আমি। তাই পাল্টা প্রশ্ন করলাম তাঁকে। আমি উল্লেখ করলাম, এগারো-মাত্রার সুপারমেমব্রেন অর্থহীন (তিনি এই তত্ত্ব সূত্রবদ্ধ করতে সহায়তা করেছেন)। কারণ, এটি গাণিতিকভাবে জটিল, এমনকি বিশ্রীও বটে। আবার এটা অস্থিতিশীলও বটে। তিনি স্বীকার করলেন, এটা একটা সমস্যাই বটে। কিন্তু এসব প্রশ্ন ভবিষ্যতে সমাধান হয়ে যাবে বলে বেশ আত্মবিশ্বাসী ছিলেন।

আমি আরও বললাম, এগারো-মাত্রার অতিমহাকর্ষ সসীম নয়, তা স্ট্রিং থিওরি বাদে অন্যান্য তত্ত্বের মতো উড়ে যাবে। তিনি শান্তস্বরে জবাব দিলেন, এটা এখন আর কোনো সমস্যা নয়। কারণ, অতিমহাকর্ষ একটা বৃহৎ তত্ত্বের ও এখনো রহস্যময় তত্ত্ব বা এম তত্ত্বের একটা আসন্নতা ছাড়া কিছু নয়। এম- তত্ত্ব সসীম। এটা আসলে মেমব্রেনের সাপেক্ষে এগারোতম মাত্রায় সূত্রবদ্ধ করা স্ট্রিং থিওরি।

এরপর বললাম, সুপারমেমব্রেন তো অগ্রহণযোগ্য। কারণ, এখনো একে কেউ ব্যাখ্যা করতে পারেনি। মেমব্রেনগুলো সংঘর্ষ হওয়ার সময় ও নতুন করে গঠিত হওয়ার সময় কীভাবে মিথস্ক্রিয়া করে (অনেক বছর আগে স্ট্রিং থিওরিবিষয়ক আমার নিজের পিএইচডি থিসিসে এটা করেছিলাম)। তিনি স্বীকার করলেন, এটা অবশ্য একটা সমস্যা। কিন্তু এটাও ভবিষ্যতে সমাধানের ব্যাপারে বেশ আত্মবিশ্বাসী দেখা গেল তাঁকে।

সবশেষে আমি বললাম, এম-তত্ত্ব আসলে কোনো তত্ত্ব নয়। কারণ, এর মৌলিক সমীকরণগুলো এখনো অজানা। স্ট্রিং থিওরির ক্ষেত্র তত্ত্ব আছে (একে সরল স্ট্রিং ক্ষেত্র সমীকরণ দিয়ে প্রকাশ করা যায়। বহু বছর আগে আমি সেগুলো লিখেছিলাম, যা গোটা তত্ত্বটার সারসংক্ষেপ)। কিন্তু স্ট্রিং থিওরির মতো মেমব্রেনের কোনো ক্ষেত্র তত্ত্ব নেই। এ বিষয়টিও তিনি মেনে নিলেন। কিন্তু এম-তত্ত্বের সমীকরণ ধীরে ধীরে খুঁজে পাওয়ার ব্যাপারে বেশ আত্মবিশ্বাসী তিনি।

আমি মনে মনে কিছুক্ষণ হাবুডুবু খেতে লাগলাম। তাঁর কথা সত্যি হলে, আরেকবার আমূল পরিবর্তনের মধ্যে যাবে স্ট্রিং থিওরি। মেমব্রেনকে একদা পদার্থবিজ্ঞানের ইতিহাসের আস্তাকুঁড়ে ছুড়ে ফেলা হয়েছিল। সেটাই হঠাৎ আবারও নতুন করে প্রাণ ফিরে পেতে লাগল।

এই বিপ্লবের উৎস হলো স্ট্রিং থিওরি তখনো পেছনের দিকে বিকশিত হচ্ছিল। এমনকি গোটা তত্ত্বটির ভিত্তি হিসেবে যে সরল ভৌত নীতি আছে, সে সম্পর্কে এখনো কেউ জানে না। একে আমি মরুভূমিতে হাঁটতে গিয়ে দুর্ঘটনাবশত একটা ছোট, সুন্দর নুড়ি পাথরের সঙ্গে হোঁচট খাওয়ার মতো কল্পনা করতে পছন্দ করি। বালু সরালে দেখা যায় সেই ছোট নুড়ি পাথরটা আসলে একটা বিশাল আকৃতির পিরামিডের শীর্ষ। সেটা টনকে টন বালুর নিচে চাপা পড়ে আছে। কয়েক দশক ধরে কষ্টকরভাবে বালু সরিয়ে আমরা একটা রহস্যময় হায়ারোগ্লিফিক, গুপ্ত কক্ষ ও সুড়ঙ্গ আবিষ্কার করেছি। একদিন হয়তো আমরা নিচতলাটাও খুঁজে পাব। তখন অবশেষে দরজাটাও খুলে দেওয়া সম্ভব হবে।

ব্রেন ওয়ার্ল্ড

এম-তত্ত্বের একটা অভিনব বৈশিষ্ট্য হলো এটা শুধু স্ট্রিংয়ের সূচনা করে না, সঙ্গে বিভিন্ন মাত্রার মেমব্রেনের আস্তানা হিসেবেও কাজ করে। এই চিত্রে বিন্দুকণাকে বলা হয় ‘জিরো ব্রেন’ বা শূন্য স্তর। কারণ, এরা অসীম পরিমাণ ক্ষুদ্র এবং এদের কোনো মাত্রাও নেই। সে ক্ষেত্রে একটা স্ট্রিং হলো ‘ওয়ান ব্রেন’ বা এক স্তরী। কারণ, এটি তার দৈর্ঘ্যের ভিত্তিতে একমাত্রিক বস্তু। একটা মেমব্রেন হলো ‘টু- ব্রেন’ বা দ্বিস্তরী। একটা বাস্কেটবলের পৃষ্ঠতলের মতো, যার দৈর্ঘ্য ও প্রস্থ থাকে। (একটা বাস্কেটবল তিন মাত্রায় ভাসতে পারে, কিন্তু এটি মাত্র দ্বিমাত্রিক। ) আমাদের মহাবিশ্ব কোনো এক ধরনের ‘ত্রি-ব্রেন’ বা ত্রিস্তরী। অর্থাৎ এটি একটা ত্রিমাত্রিক বস্তু, যার দৈর্ঘ্য, প্রস্থ ও বেধ আছে। (একজন রসিকতা করে বলেছিল, স্থানের যদি পি (p) মাত্রা থাকে এবং পি যদি পূর্ণসংখ্যা হয়, তাহলে আমাদের মহাবিশ্ব হলো একটা পি-ব্রেন। একে উচ্চারণ করা হয় পি-ব্রেইন। যে তালিকায় সবগুলো পি-ব্রেইন দেখানো হয়, তাকে বলা হয় ব্রেইন-স্ক্যান। )

কিছু উপায়ে আমরা একটা মেমব্রেন নিয়ে তা ভেঙে একটা স্ট্রিং পেতে পারি। এগারোতম মাত্রা মুড়ে দেওয়ার বদলে একটা এগারো-মাত্রিক মেমব্রেনের মেরু কেটে ফেলে একটা বৃত্তাকার ফিতা তৈরি করা যায়। ফিতাটিকে সংকুচিত হয়ে ঘনবদ্ধ হতে দিলে ফিতাটি পরিণত হবে একটা দশ- মাত্রিক স্ট্রিংয়ে। পেতর হোরাভা এবং এডওয়ার্ড উইটেন দেখিয়েছেন, আমরা এভাবে হেটারোটিক স্ট্রিং পাই।

আসলে এটাও দেখানো যায় যে এগারো-মাত্রিক এম-তত্ত্বকে কমিয়ে দশ মাত্রায় নামিয়ে আনার পাঁচটি উপায় আছে। এভাবে আমরা পাঁচটি সুপারস্ট্রিং থিওরি পেতে পারি। পাঁচটি ভিন্ন ভিন্ন স্ট্রিং থিওরি থাকার কারণ কী, সে ব্যাপারে আমাদের একটা দ্রুত, অন্তজ্ঞানমূলক উত্তর দেয় এম-তত্ত্ব। একটা বড় পাহাড়চূড়ার ওপর দাঁড়িয়ে নিচের সমতলের দিকে তাকিয়ে থাকার কথা একবার কল্পনা করুন। তৃতীয় মাত্রার এই সুবিধাজনক জায়গা থেকে আমরা সমতলভূমির বিভিন্ন অংশকে একটা একীভূত সংহতিপূর্ণ ছবি হিসেবে দেখতে পাই। ঠিক যেন এগারোতম মাত্রার সুবিধাজনক জায়গা থেকে নিচের দশম মাত্রা দেখার মতো ব্যাপার। আমরা আসলে পাঁচটি সুপারস্ট্রিং থিওরির আজব কাঁথার এগারোতম মাত্রার বিভিন্ন সেলাই করা তালির মতো ছাড়া আর কিছুই দেখি না।

দ্বৈততা

সেদিন পল টাউনসেন্ড আমার করা বেশির ভাগ প্রশ্নের উত্তর না দিলেও আমি বুঝতে পেরেছি, এই ধারণার যথার্থতা ছিল আরও অন্য কোনো সিমেট্রির শক্তি। পদার্থবিজ্ঞানে শুধু এম-তত্ত্বেরই সবচেয়ে বড় প্রতিসাম্য সমষ্টি আছে, তা সঠিক নয়। তবে এর আরও কিছু কৌশল আছে। এর মধ্যে অন্যতম হলো ডুয়ালিটি বা দ্বৈততা। এটিই এম-তত্ত্বকে পাঁচটি সুপারস্ট্রিং থিওরির সবগুলোকে শোষণ করে একটা তত্ত্বে নিয়ে আসার রহস্যময় ক্ষমতা দিয়েছে।

বিদ্যুৎ ও চুম্বকত্বের কথা বিবেচনা করুন। এখানে কাজ করে ম্যাক্সওয়েলের সমীকরণ। অনেক আগে থেকে বোঝা গিয়েছিল যে বৈদ্যুতিক ক্ষেত্রকে কোনো চুম্বকীয় ক্ষেত্রের সঙ্গে বিনিময় করলে সমীকরণগুলোর চেহারা প্রায় একই থাকে। এখানে প্রতিসাম্যতা একেবারে হুবহু থাকে, যদি ম্যাক্সওয়েলর সমীকরণে মনোপল বা একমেরুত্ব (চুম্বকীয় এক মেরু) যোগ করা যায়। বৈদ্যুতিক ক্ষেত্রের সঙ্গে চুম্বকীয় ক্ষেত্র বিনিময় করলে এবং বৈদ্যুতিক চার্জ e-এর সঙ্গে চুম্বকীয় চার্জ g-এর বিপরীতমুখিতা আন্তবিনিময় করা হলে ম্যাক্সওয়েলের সমীকরণগুলো যথাযথভাবে একই থাকবে। এর মানে, বিদ্যুৎ (যদি বৈদ্যুতিক চার্জ কম থাকে) যথাযথভাবে চুম্বকের সমতুল্য (যদি চুম্বকীয় চার্জ বেশি থাকে)। এই সমতুল্যতাকে বলা হয় ডুয়ালিটি বা দ্বৈততা।

অতীতে এই দ্বৈততাকে একটা বৈজ্ঞানিক কৌতূহলের চেয়ে বেশি কিছু ভাবা হয়নি। কারণ, কেউই এখন পর্যন্ত মনোপোল দেখেনি। তবে পদার্থবিদেরা একটা ব্যাপার লক্ষ করেছেন, ম্যাক্সওয়েলের সমীকরণে একটা গোপন প্রতিসাম্যতা আছে, যা প্রকৃতি দৃশ্যত ব্যবহার করে না (অন্তত মহাবিশ্বের আমাদের এই এলাকায়)

একইভাবে পাঁচটি স্ট্রিং থিওরির সবগুলো পরস্পরের দ্বৈত। টাইপ ওয়ান ও হেটারোটিক SO(32) স্ট্রিং থিওরির কথা ভাবুন। সাধারণত এই দুটি তত্ত্ব কখনো দেখতে একই মনে হয় না। টাইপ ওয়ান থিওরির ভিত্তি উন্মুক্ত ও বদ্ধ স্ট্রিং, যা পাঁচটি ভিন্ন উপায়ে মিথস্ক্রিয়া করতে পারে। এখানে স্ট্রিং আলাদা হয়ে যায় ও জোড়া লাগে। অন্যদিকে SO(32) স্ট্রিংয়ের ভিত্তি পুরোটাই বদ্ধ স্ট্রিং, যার একটামাত্র সম্ভাব্য মিথস্ক্রিয়ার উপায় আছে। সেটা একটা জীবকোষের মাইটোসিস প্রক্রিয়ায় মতো বিভাজিত হওয়া। টাইপ ওয়ান স্ট্রিংকে পুরোপুরি দশ-মাত্রিক স্থানে সংজ্ঞায়িত করা হয়। অন্যদিকে SO(32) স্ট্রিংকে সংজ্ঞায়িত করা হয় ২৬-মাত্রিক স্থানের এক গুচ্ছ কম্পনের সঙ্গে।

সাধারণত আমরা দুটি তত্ত্বের মধ্যে কোনো বৈসাদৃশ্য খুঁজে পাই না। তবে বিদ্যুৎ-চুম্বকীয়র মতো এই তত্ত্বগুলোরও একটা শক্তিশালী দ্বৈততা আছে। মিথস্ক্রিয়ার শক্তিমত্তা বাড়ার সুযোগ দেওয়া হলে টাইপ ওয়ান স্ট্রিং SO (32) হেটারোটিক স্ট্রিংয়ে বদলে যায়, ঠিক ভোজবাজির মতো। (এই ফলাফল এতই অপ্রত্যাশিত যে আমি প্রথম এই ফলাফল দেখে চরম বিস্ময় মাথা নাড়াতে বাধ্য হয়েছিলাম। পদার্থবিজ্ঞানে সব দিক দিয়ে দৃশ্যত বৈসাদৃশ্য দুটি তত্ত্বকে গাণিতিভাবে সমতুল্য দেখাতে পাওয়াটা বিরল ঘটনা।)

লিসা র‍্যান্ডেল

সবচেয়ে বড় সুবিধাটা সম্ভবত স্ট্রিং থিওরির চেয়ে এম-তত্ত্বে এসব উচ্চতর মাত্রা থাকে। সেগুলো ছোট নয়, বেশ বড়; এমনকি তা গবেষণাগারে পরীক্ষাযোগ্য। স্ট্রিং থিওরিতে উচ্চতর মাত্রাগুলোর মধ্যে ছয়টি অবশ্যই একটা খুদে বলের মধ্যে কুঁকড়ে থাকে। একে বলা হয় কালাবি-ইয়াউ ম্যানিফোল্ড। এগুলো এত ছোট যে বর্তমানের প্রচলিত যন্ত্রপাতি দিয়ে তাদের পর্যবেক্ষণ করা সম্ভব নয়। এ ছয় মাত্রার সবগুলোই নিবিড়ভাবে থাকে। তাই কোনো উচ্চতর মাত্রায় ঢোকা অসম্ভব। যারা ভবিষ্যতের কোনো একদিন ওয়ার্মহোলের কমপ্যাক্টিফায়েড হাইপারস্পেসের ভেতর দিকে সংক্ষিপ্ত শর্টকাট না নিয়ে কোনো অসীম হাইপারস্পেসে ভাসার আশা করে, তাদের জন্য এটা বেশ হতাশাজনক।

তবে এম-তত্ত্বের মেমব্রেনের বৈশিষ্ট্যও আছে। আমাদের গোটা মহাবিশ্বকে অন্য আরেকটা বড়সড় মহাবিশ্বের ভেতর একটা মেমব্রেনের মতো ভেসে আছে—এমন চিন্তা করাও সম্ভব। ফলে ওই উচ্চতর মাত্রার সবগুলোই কোনো বলের মধ্যে কুঁকড়ে যাবে না। তাদের কয়েকটি আসলে বেশ বড় হবে। সেগুলো অসীম পর্যন্তও বিস্তৃত হতে পারে।

মহাবিশ্বের নতুন এই চিত্রটি কাজে লাগানোর চেষ্টা করা করছেন হার্ভার্ডের পদার্থবিদ লিসা র‍্যান্ডেল। তার চেহারা অভিনেত্রী জোডি ফস্টারের মতো। তীব্র প্রতিযোগিতাময়, টেস্টোটেরন-চালিত, প্রবলভাবে পুরুষশাসিত তাত্ত্বিক পদার্থবিজ্ঞানের বাইরের কেউ বলে মনে হয় র‍্যান্ডেলকে। মহাবিশ্ব সত্যিই উচ্চতর মাত্রার স্থানে ভাসমান একটা তিন-ব্রেন হলে অন্যান্য তিনটি বলের চেয়ে মহাকর্ষ এত বেশি দুর্বল কেন, তা হয়তো ব্যাখ্যা করা যাবে। এই আইডিয়া নিয়েই কাজ করেছেন তিনি।

র‍্যান্ডেল বেড়ে উঠেছেন নিউইয়র্কের কুইন্সে (নিউইয়র্কের এই নগরটি আর্চি বাঙ্কারের কারণে অমর হয়ে আছে)। শৈশবে পদার্থবিজ্ঞানের প্রতি তাঁর বিশেষ কোনো আগ্রহ দেখা যায়নি। অবশ্য আমি বিশ্বাস করি, শিশু অবস্থায় আমরা সবাই একেকজন বিজ্ঞানী হিসেবেই জন্ম নিই। তবে বড় হওয়ার পর সবাই বিজ্ঞানের প্রতি সেই ভালোবাসাটা আর ধরে রাখতে পারি না। এর অন্যতম কারণ হলো, আমরা একসময় গণিতের শক্ত দেয়ালে ধাক্কা খাই।

আমরা পছন্দ করি বা না করি, বিজ্ঞানে ক্যারিয়ার গড়তে চাইলে একসময় অবশ্যই প্রকৃতির ভাষা বা গণিত শিখতে হবে। গণিত ছাড়া প্রকৃতির নৃত্যে সক্রিয় অংশীদার না হয়ে কেবল পরোক্ষ দর্শক হয়ে থাকতে হবে। আইনস্টাইন বলেছিলেন, ‘বিশুদ্ধ গণিত হলো, তার নিজের পথে যৌক্তিক ধারণার কাব্য।’ আরেকটা তুলনা করা যাক। অনেকেই হয়তো ফরাসি সভ্যতা ও সাহিত্যের ভক্ত। কিন্তু ফরাসিদের মন সত্যিকারভাবে বুঝতে হলে তাকে অবশ্যই ফরাসি ভাষা ও ফরাসি ক্রিয়াপদের ধাতুরূপ শিখতে হবে। একই কথা খাটে বিজ্ঞান আর গণিতের বেলাতেও। গ্যালিলিও একবার লিখেছিলেন, ভাষা না শিখে [মহাবিশ্ব] পড়া যায় না। এটি লেখা হয়েছে গণিতের ভাষায়। বর্ণগুলো লেখা হয়েছে ত্রিভুজ, বৃত্ত ও অন্যান্য জ্যামিতিক আদলে। এগুলো ছাড়া এক বর্ণও বোঝা মানুষের পক্ষে সম্ভব নয়।’

কিন্তু সব বিজ্ঞানীর মধ্যে নিজেদের সবচেয়ে অপ্রায়োগিক বলে আত্মতৃপ্তিতে ভোগেন গণিতবিদেরা। গণিত যত বিমূর্ত ও অকেজো হয়, ততই যেন ভালো। ১৯৮০-এর দশকে হার্ভার্ডে আন্ডারগ্র্যাজুয়েট করার সময় একটা কারণে ভিন্ন দিকে যাওয়ার কথা ভাবেন র‍্যান্ডেল। সেটা হলো, পদার্থবিজ্ঞান মহাবিশ্বের বিভিন্ন মডেল তৈরি করতে পারে। এটাই বেশ পছন্দ হলো তাঁর। আমরা পদার্থবিদেরা যখন নতুন তত্ত্বের প্রস্তাব করি, সেগুলোর সাধারণত ভিত্তি একগুচ্ছ সমীকরণ। নতুন ভৌত তত্ত্ব সচরাচর সরল, আদর্শ মডেলের ওপর ভিত্তি করে গড়ে ওঠে, যা একটা পরিঘটনার আসন্নতা। এসব মডেল সাধারণ গ্রাফসংবলিত, চিত্রভিত্তিক ও সহজে বোধগম্য। যেমন ধরা যাক, কোয়ার্ক মডেল গড়ে উঠেছে এই ধারণার ওপর—প্রোটনের মধ্যে তিনটি ছোট ছোট উপাদান থাকে। এদের বলা হয় কোয়ার্ক। মহাবিশ্বের অনেকখানি ব্যাখ্যা করতে পারা এসব ভৌত চিত্রভিত্তিক এই সরল মডেল দেখে মুগ্ধ হন র‍্যান্ডেল।

১৯৯০-এর দশকে এম-তত্ত্বে আগ্রহী হন তিনি। কারণ, গোটা মহাবিশ্ব একটা মেমব্রেন হওয়ার সম্ভাবনা চোখে পড়ে র‍্যান্ডেলের। মহাকর্ষের সম্ভবত সবচেয়ে গোলমেলে ধর্ম তার শক্তিমত্তা স্বয়ংক্রিয়ভাবে অনেক ছোট। এদিকে মনোযোগী হয়ে ওঠেন তিনি। নিউটন কিংবা আইনস্টাইন কেউই এই মৌলিক ও রহস্যময় প্রশ্নের জবাব দিতে পারেননি। মহাবিশ্বের অন্য তিনটি বলের (বিদ্যুৎ-চুম্বকীয়, দুর্বল নিউক্লিয়ার বল ও সবল নিউক্লিয়ার বল) শক্তিমত্তা যেখানে মোটামুটি প্রায় একই, সেখানে মহাকর্ষ বেপরোয়া রকম আলাদা।

বিশেষ করে বলতে গেলে, কোয়ান্টাম মহাকর্ষের সঙ্গে সম্পর্কিত ভরের তুলনায় কোয়ার্কদের ভর খুব কম। ‘এই অসংগতি মোটেও হেলাফেলা করার মতো নয়। দুটি ভরের মাপদণ্ড ১০^১৬ গুণ আলাদা! যেসব তত্ত্ব শুধু এই বিপুল অনুপাত ব্যাখ্যা করে, তারা হয়তো স্ট্যান্ডার্ড মডেলের অন্তর্নিহিত তত্ত্বগুলোর প্রার্থী হতে পারে।’, বলেন লিসা র‍্যান্ডাল।

মহাকর্ষ এতটা দুর্বল হওয়ার জন্যই ‘নক্ষত্ররা এত বড় হয় কেন’, তা ব্যাখ্যা করা যায়। বিপুল আকৃতির সূর্যের তুলনায় পৃথিবী, তার সাগর- মহাসাগর, পাহাড়-পর্বত আর মহাদেশ একটা খুদে কণা ছাড়া কিছুই নয়। কিন্তু মহাকর্ষ এত দুর্বল বলেই, হাইড্রোজেন চেপে ধরার জন্য গোটা নক্ষত্রের সমান ভরের প্রয়োজন হয়। ফলে তা প্রোটনের বৈদ্যুতিক বলের বিকর্ষণের বিরুদ্ধে টেক্কা দিতে পারে। কাজেই নক্ষত্ররা বিপুল ভরের হয়, কারণ অন্যান্য বলের সঙ্গে তুলনা করলে মহাকর্ষ অতি দুৰ্বল।

এম-তত্ত্ব পদার্থবিজ্ঞানে এতই উত্তেজনার জন্ম দিয়েছে যে এই তত্ত্বটিকে আমাদের মহাবিশ্বে প্রয়োগের চেষ্টা করে দেখছেন বেশ কটি দল। মহাবিশ্ব পাঁচ-মাত্রিক একটা বিশ্বের ভেতর একটা তিন-ব্রেন ভাসমান বলে ধরে নেওয়া হয়েছে। এবার তিন-ব্রেনের পৃষ্ঠতলের কম্পন আমাদের চারপাশের পরমাণুর সঙ্গে জড়িত। কাজেই এসব কম্পন কখনো তিন-ব্রেন ছেড়ে চলে যায় না। আবার তাতে তা চলে যেতে পারে না পঞ্চম মাত্রাতেও। এমনকি আমাদের মহাবিশ্ব পঞ্চম মাত্রার ভেতর ভাসমান হলেও আমাদের পরমাণুগুলো আমাদের মহাবিশ্ব ছেড়ে চলে যায় না। কারণ, পরমাণুগুলো তিন-ব্রেনের পৃষ্ঠতলের ওপর কম্পনের প্রতীক। তাহলে এর মাধ্যমে কালুজা এবং আইনস্টাইনের ১৯২১ সালে করা সেই প্রশ্নের উত্তর পাওয়া যায় : পঞ্চম মাত্রাটি কোথায়? এর উত্তর হলো : আমরা একটা পঞ্চম মাত্রায় ভাসছি, কিন্তু এর ভেতর ঢুকতে পারছি না। কারণ, আমাদের দেহ একটা তিন-ব্রেনের পৃষ্ঠতলে আটকে গেছে।

কিন্তু এই চিত্রে সম্ভাব্য একটা ত্রুটিও আছে। মহাকর্ষ আসলে স্থানের বক্রতার প্রতীক। কাজেই আমরা অকপটে আশা করতে পারি, মহাকর্ষ শুধু তিন-ব্রেন নয়, বরং পাঁচ-মাত্রিক স্থানের পুরোটা পূরণ করতে পারবে। সেটি করতে গিয়ে তিন-ব্রেন ছেড়ে যেতে হালকা হয়ে যাবে মহাকর্ষ বল। ফলে মহাকর্ষ বল দুর্বল হয়ে যাবে। এ তত্ত্বের সমর্থনে এটা বেশ ভালো ব্যাপার। কারণ, আমরা জানি, মহাকর্ষ অন্য বলগুলোর চেয়ে অনেক অনেক দুর্বল। কিন্তু এটা মহাকর্ষকে অনেক বেশি দুর্বল করে দেবে: নিউটনের বিপরীত বর্গীয় সূত্র তাতে লঙ্ঘিত হবে। কিন্তু তারপরও বিপরীত বর্গীয় সূত্রটি সঠিকভাবে কাজ করবে গ্রহ, নক্ষত্র ও ছায়াপথের জন্য। স্থানের কোথাও মহাকর্ষের জন্য বিপরীত ঘনক্ষেত্রের সূত্র খুঁজে পাওয়া যায় না। (একটা ঘরকে আলোকিত করে রাখা একটা লাইটবাল্বের কথা ভাবুন। আলো গোলকীয়ভাবে ছড়িয়ে পড়বে। এই গোলকজুড়ে হালকা হয়ে যাবে আলোর শক্তিমত্তা। কাজেই এই গোলকের ব্যাসার্ধ দ্বিগুণ করা হলে আলো ছড়িয়ে পড়বে চারগুণ ক্ষেত্রফল এলাকায়। সাধারণভাবে একটা লাইটবাল্ব যদি n- মাত্রিক স্থানে থাকে, তাহলে তার আলো যে গোলকজুড়ে হালকা হবে, তার ক্ষেত্রফল বাড়বে তার ব্যাসার্ধ n^-1 ঘাতে বাড়ার হারে।)

এই প্রশ্নের উত্তর দিতে চেষ্টা করেছেন একদল পদার্থবিদ। এ দলে আছে এন আরকানিহামাদ, এস ডাইমোপোলস এবং জি ভালি। তাদের প্রস্তাব, সম্ভবত পঞ্চম মাত্রা অসীম নয়, বরং আমাদের কাছে থেকে এক মিলিমিটার দূরে অবস্থিত, যা আমাদের মহাবিশ্বের ঠিক ওপরে ভাসছে। ঠিক এইচ জি ওয়েলসের বিজ্ঞান কল্পকাহিনির মতো। (পঞ্চম মাত্রা এক মিলিমিটারের বেশি দূরে হলে সেটা হয়তো নিউটনের বিপরীত বর্গীয় সূত্রের একটা পরিমাপযোগ্যভভাবে লঙ্ঘন করতে পারে।) পঞ্চম মাত্রা এক মিলিমিটার দূরে হলে, ছোট দূরত্বে নিউটনের মহাকর্ষ সূত্রের ক্ষুদ্র বিচ্যুতি দেখে এই ভবিষ্যদ্বাণী পরীক্ষা করে দেখা সম্ভব। অনেক বড় দূরত্বেরও বেশ নিখুঁতভাবে কাজ করে নিউটনের মহাকর্ষ সূত্র। কিন্তু একে কখনো এক মিলিমিটার পরিসরে পরীক্ষা করে দেখা হয়নি। পরীক্ষকেরা এখন নিউটনের বিপরীত বর্গীয় সূত্র থেকে ক্ষুদ্র বিচ্যুতি পরীক্ষার জন্য ব্যস্তভাবে ছুটতে শুরু করেছেন। এই ফলাফলটি বর্তমানে বেশ কয়েকটি চলমান পরীক্ষার বিষয়। সে বিষয়ে নবম অধ্যায়ে আমরা দেখতে পাব।

পঞ্চম মাত্রাটি এক মিলিমিটার দূরে অবস্থিত নয়, হয়তো তা অসীম দূরত্বে—এই সম্ভাবনা খতিয়ে দেখতে নতুন একটা পদ্ধতি অবলম্বনের সিদ্ধান্ত নেন র‍্যান্ডাল ও তাঁর সহকর্মী রমন সুন্দ্রম। সেটি করতে তাঁদের ব্যাখ্যা করতে হয়েছিল, পঞ্চম মাত্রা নিউটনের মহাকর্ষ সূত্র নষ্ট না করে কীভাবে অসীমে বিস্তৃত থাকতে পারে। এখানেই ধাঁধাটির একটা সম্ভাব্য উত্তর খুঁজে পান র‍্যান্ডাল। তিনি দেখতে পান, তিন-ব্রেনের একটা নিজস্ব মহাকর্ষীয় টান আছে, যেটি গ্র্যাভিটনকে পঞ্চম মাত্রায় অবাধে প্রবাহিত হতে বাধা দেয়। গ্র্যাভিটন তিন-ব্রেনে দৃঢ়ভাবে আটকে থাকে (অনেকটা ফ্লাইপেপারে আটকে পড়া মাছির মতো)। কারণ, তিন-ব্রেন মাধ্যমে মহাকর্ষ বিস্তৃত হয়। কাজেই নিউটনের সূত্র মাপার চেষ্টা করলে দেখা যায় যে তা আমাদের মহাবিশ্বে সঠিকের কাছাকাছি। তিন-ব্রেন থেকে বেরিয়ে এলে ও পঞ্চম মাত্রায় এসে মহাকর্ষ হালকা আর দুর্বল হয়ে যায়। কিন্তু তা খুব বেশি দূর যেতে পারে না। বিপরীত বর্গীয় সূত্র তখনো মোটা দাগে রক্ষিত হয়। কারণ, তিন-ব্রেনের প্রতিও মহাকর্ষ আকর্ষীধৰ্মী। (আবার আমাদের সঙ্গে সমান্তরালভাবে দ্বিতীয় আরেকটা মেমব্রেন থাকার সম্ভাবনার সঙ্গে পরিচয় করিয়ে দেন র‍্যান্ডাল। এই দুই মেমব্রেনজুড়ে মহাকর্ষের অতি

সূক্ষ্ম মিথস্ক্রিয়া যদি গণনা করা হয়, তাহলে তা সংখ্যাগতভাবে মহাকর্ষের দুর্বলতার ব্যাখ্যা করতে পারার মতো করে খাপ খায় না।)

‘অতিরিক্ত মাত্রা [হায়ারকি সমস্যার] উৎসের জন্য বিকল্প উপায়ের জোগান দেয়, সেটা প্রথম প্রস্তাব করার সময় ব্যাপক উত্তেজনা দেখা দিয়েছিল।’ র‍্যান্ডাল বলেন। ‘অতিরিক্ত স্থানিক মাত্রা দেখতে হয়তো প্রথমে কোনো খ্যাপাটে ধারণা বলে মনে হতে পারে, কিন্তু দৃঢ় কিছু কারণে বিশ্বাস করতে হবে যে এখানে আসলে স্থানের অতিরিক্ত মাত্রা আছে।’

এই পদার্থবিদদের কথা সঠিক হলে, মহাকর্ষও আসলে অন্যান্য বলের মতো শক্তিশালী। এখানে ব্যতিক্রম শুধু এই যে মহাকর্ষ ক্ষয় হয়ে যায়। কারণ, এর কিছু অংশ লিক হয়ে যায় উচ্চতর মাত্রিক স্থানে। এই তত্ত্বের একটা গভীর পরিণতি হলো, শক্তি দশায় এসব কোয়ান্টাম প্রভাব পরিমাপযোগ্য, তা হয়তো আগের ভাবনার মতো প্ল্যাঙ্ক শক্তি নয় (১০^১৯ বিলিয়ন ইলেকট্রন ভোল্ট)। সম্ভবত কয়েক ট্রিলিয়ন ইলেকট্রন ভোল্ট দরকার হতে পারে। সে ক্ষেত্রে চলতি দশকের মধ্যে কোয়ান্টাম মহাকর্ষীয় প্রভাব অর্জন করতে সক্ষম হবে লার্জ হ্যাড্রন কলায়ডার। স্ট্যান্ডার্ড মডেলের অতিপারমাণবিক কণার বাইরে বিচিত্র কণার সন্ধানে এই পরীক্ষণ বেশ আগ্রহ জাগিয়ে তুলতে পেরেছে পদার্থবিদদের মধ্যে। হয়তো কোয়ান্টাম মহাকর্ষীয় প্রভাব কিছু দিনের মধ্যে আমাদের হাতের নাগালে চলে আসবে।

আবার ডার্ক ম্যাটার বা গুপ্তবস্তুর রহস্য বিষয়ে কিছুটা অনুমানমূলক হলেও একটা যুক্তিসংগত জবাব দেয় মেমব্রেন। এইচ জি ওয়েলসের দ্য ইনভিজিবল ম্যান উপন্যাসে মূল চরিত্র চতুর্থ মাত্রার মধ্যে ভাসছিল। সে জন্যই সবার চোখে অদৃশ্য হয়ে ছিল সে। একইভাবে কল্পনা করা যাক, আমাদের নিজেদের মহাবিশ্বের ঠিক ওপরে একটা সমান্তরাল মহাবিশ্ব ভেসে আছে। এই সমান্তরাল মহাবিশ্বের যেকোনো ছায়াপথ আমাদের কাছে অদৃশ্য হয়ে থাকবে।

কিন্তু হাইপারস্পেসের বক্রতার কারণে যেহেতু মহাকর্ষ সৃষ্টি হয়, তাই মহাকর্ষ এ মহাবিশ্ব থেকে ও মহাবিশ্বের মধ্যে ছড়িয়ে যেতে পারবে। এই মহাবিশ্বের যেকোনো বড় ছায়াপথ হাইপারস্পেসজুড়ে আমাদের মহাবিশ্বের কোনো ছায়াপথের দিকে আকৃষ্ট হবে। তাতে দেখা যাবে, তাদের মহাকর্ষীয় টান নিউটনের সূত্রের প্রত্যাশার চেয়েও অনেক বেশি শক্তিশালী। কারণ, এর পেছনে আরেকটি ছায়াপথ লুকিয়ে আছে, যা হয়তো পার্শ্ববর্তী কোনো ব্রেনে ভাসছে। আমাদের ছায়াপথের ওপরের এই গোপন ছায়াপথ হয়তো পুরোপুরি অদৃশ্য হবে। কারণ, তা আরেকটি মাত্রায় ভেসে আছে। কিন্তু এটি আমাদের ছায়াপথের চারপাশে ৯০ ভাগ ভরসম্পন্ন একটা বলয় হিসেবে আবির্ভূত হবে। কাজেই গুপ্তবস্তুর উপস্থিতির কারণ হয়তো কোনো সমান্তরাল মহাবিশ্ব।

সংঘর্ষমুখী মহাবিশ্ব

গুরুতরভাবে কসমোলজিতে এম-তত্ত্ব ব্যবহার করা হয়তো কিছুটা আগাম হয়ে যেতে পারে। তারপরও ‘ব্রেন পদার্থবিদ্যা’ ব্যবহার করে মহাবিশ্বের জন্য প্রচলিত স্ফীতি তত্ত্বের পদ্ধতিতে নতুন মোড় তৈরির চেষ্টা করছেন পদার্থবিদেরা। তিনটি সম্ভাব্য কসমোলজির ক্ষেত্রে এটা কিছুটা দৃষ্টি আকর্ষণ করতে পেরেছে।

প্রথম ক্ষেত্রে এটা কসমোলজির একটা প্রশ্নের উত্তর দেওয়ার চেষ্টা করেছে : আমরা চার মাত্রিক স্থান-কালে বাস করি কেন? তাত্ত্বিকভাবে, এম-তত্ত্ব এগারো মাত্রা পর্যন্ত সব মাত্রায় সূত্রবদ্ধ করা যায়। কাজেই চার মাত্রা বেছে নেওয়ার ব্যাপারটা মনে হয় বেশ রহস্যজনক। রবার্ট ব্র্যান্ডেনবার্গার এবং কামরান ভাফার অনুমান, হয়তো স্ট্রিংয়ের বিশেষ কোনো জ্যামিতির কারণে এটা হতে পারে।

এই চিত্রে, মহাবিশ্বের শুরুটা হয়তো হয়েছিল নিখুঁত প্রতিসাম্যতার মধ্যে দিয়ে। সেখানে সব উচ্চতর মাত্রা দৃঢ়ভাবে প্ল্যাঙ্ক স্কেলে কুঁকড়ে ছিল। এ সময় মহাবিশ্বকে প্রসারিত হতে বাধা দিয়েছিল, স্ট্রিংয়ের লুপ, যা দৃঢ়ভাবে কুঁকড়ে ছিল বিভিন্ন মাত্রার চারদিকে। প্রসারিত হতে পারে না, এমন একটা সংকুচিত কয়েলের কথা চিন্তা করুন। কারণ, তা স্ট্রিংয়ের মাধ্যমে দৃঢ়ভাবে আবদ্ধ। স্ট্রিংগুলো যদি কোনোভাবে ভেঙে যায়, তখন কয়েলটি হঠাৎ করে মুক্ত হয়ে লাফিয়ে উঠবে এবং প্রসারিত হতে থাকবে।

এই ক্ষুদ্র মাত্রাগুলোতে মহাবিশ্বকে প্রসারিত হতে বাধা দেওয়া হয়েছিল। কারণ, আমাদের কাছে এলোমেলো বা ঝোড়ো স্ট্রিং ও অ্যান্টিস্ট্রিং উভয়ই ছিল (মোটা দাগে বললে, অ্যান্টিস্ট্রিং বক্রতা/বাতাস হলো বিপরীত দিক থেকে আসা স্ট্রিং)। একটা স্ট্রিং আরেকটা অ্যান্টিস্ট্রিংয়ের সঙ্গে সংঘর্ষ হলে সেটা নিশ্চিহ্ন হয়ে অদৃশ্য হয়ে যেতে পারে। অনেকটা একটা সুতার গিঁট বা পাক খোলার মতো করে। অনেক বড় মাত্রাগুলোতে এত বেশি জায়গা থাকে যে স্ট্রিং আর অ্যান্টিস্ট্রিংয়ের সংঘর্ষ হওয়ার ঘটনা বিরল। আবার তাদের পাকও খোলে না। তবে ব্রানডেনবার্গার এবং ভাফা দেখিয়েছেন, তিনটি বা তার চেয়ে কম স্থানিক মাত্রায় অ্যান্টিস্ট্রিংয়ের সঙ্গে স্ট্রিংগুলোর সংঘর্ষ ঘটার সম্ভাবনা বেশি। একবার এই সংঘর্ষ ঘটলে স্ট্রিংয়ের পাক খুলে যায় এবং এ মাত্রাগুলো দ্রুত বাইরে চলে গিয়ে আমাদের মহাবিস্ফোরণ উপহার দেয়। এই চিত্রের আকর্ষণীয় দিক হলো, স্ট্রিংয়ের টপোলজি মোটামুটিভাবে ব্যাখ্যা করতে পারে, আমরা কেন চারপাশে পরিচিত স্থান-কালের মাত্রা দেখতে পাই। উচ্চ-মাত্রিক মহাবিশ্বগুলোও সম্ভব, কিন্তু সেগুলো দেখার সম্ভাবনা কম। কারণ, তারা দৃঢ়ভাবে স্ট্রিং আর অ্যান্টিস্ট্রিংয়ের মাধ্যমে আবদ্ধ হয়ে আছে।

তবে এখানে এম-তত্ত্বে আরও কিছু সম্ভাবনা আছে। মহাবিশ্বগুলো যদি পরস্পরকে চেপে ধরে কিংবা কুড়ি থেকে অঙ্কুরিত করে নতুন মহাবিশ্বের জন্ম দেয়, তাহলে হয়তো এর উল্টোটাও ঘটা সম্ভব। অর্থাৎ মহাবিশ্বগুলোর মধ্যে সংঘর্ষ ঘটে এ প্রক্রিয়ায় স্ফুলিঙ্গ তৈরি হলো এবং এরপর নতুন মহাবিশ্বের জন্ম হলো। এই চিত্রে মহাবিস্ফোরণ সংঘটিত হওয়ার কারণ হয়তো একটা মহাবিশ্বের কুঁড়ি থেকে অঙ্কুরিত না হয়ে দুটি সমান্তরাল ব্রেন-মহাবিশ্বের সংঘর্ষ।

দ্বিতীয় তত্ত্বটির প্রস্তাব করেছিলেন প্রিন্সটনে পল স্ট্রেইনহার্ট, পেনসিলভানিয়া বিশ্ববিদ্যালয়ের বার্ট ওভুরাট এবং কেমব্রিজ বিশ্ববিদ্যালয়ের নিল টুরোক। এম-ব্রেনের অভিনব বৈশিষ্ট্যের সঙ্গে সম্পর্কযুক্ত করতে ‘ইকপাইরোটিক’ মহাবিশ্বের (গ্রিক ভাষায় যার অর্থ দাবানল) জন্ম দিয়েছিলেন তাঁরা। এতে অতিরিক্ত কিছু মাত্রা আকারে বেশ বড় ও এমনকি অসীমও হতে পারে। দুটি সমতল, সমজাতীয় আর সমান্তরাল তিন-ব্রেন দিয়ে এগুলো শুরু হয়। এগুলো সর্বনিম্ন শক্তি অবস্থার প্রতীক। মূলত, তাদের শুরু হয় শূন্য ও শীতল মহাবিশ্ব হিসেবে। তবে মহাকর্ষ তাদের পরস্পরের দিকে টানতে থাকে। এতে ক্রমেই তাদের সংঘর্ষ হয় এবং এ সংঘর্ষের বিপুল গতিশক্তি রূপান্তরিত হয় পদার্থ ও বিকিরণে। এগুলোই আমাদের মহাবিশ্বের জন্ম দেয়। অনেকে একে বিগ ব্যাং থিওরির বদলে বিগ স্প্যাল্ট থিওরি বলে ডাকেন। কারণ, এই সংঘর্ষ দুটি ব্রেনের সঙ্গে সম্পর্কিত।

এই সংঘর্ষের বল দুটি মহাবিশ্বকে আলাদা করে ফেলে। দুটি ব্রেন পরস্পর থেকে আলাদা হয়ে যাওয়ার পর তারা শিগগিরই শীতল হতে থাকে। এরপর বর্তমানে আমরা যে মহাবিশ্ব দেখি, তাতে পরিণত হয়। শীতলীকরণ ও প্রসারণ চলতে থাকে কয়েক ট্রিলিয়ন বছর ধরে। এই প্রসারণ চলতে থাকে মহাবিশ্ব পরম শূন্য তাপমাত্রায় না আসা পর্যন্ত। আবার এর ফলে ঘনত্ব দাঁড়ায় স্থানের প্রতি কোয়াড্রিলিয়ন (১০^১৫)ঘন আলোকবর্ষে মাত্র একটা ইলেকট্রন। ফলাফল হিসেবে মহাবিশ্ব শূন্য ও জড় হয়ে যায়। কিন্তু মহাকর্ষ দুটি মেমব্রেনকে আকর্ষণ করতে থাকে। কয়েক ট্রিলিয়ন বছর পর তাদের মধ্যে আবারও সংঘর্ষ না হওয়া পর্যন্ত চলতে থাকে এই আকর্ষণপ্রক্রিয়া। এরপর আবারও প্রথম থেকে শুরু হয় গোটা চক্রটা।

নতুন এই মডেলটি স্ফীতি তত্ত্বের (মসৃণ বা সমতল ও অভিন্নতা) জন্য বেশ ভালো ফলের জোগান দেয়। মহাবিশ্ব এত মসৃণ কেন, সেই প্রশ্নের সমাধান করে এটা। এ চিত্রমতে, এর কারণ হলো দুটি ব্রেন মসৃণ বা সমতল হিসেবে যাত্রা শুরু করে। আবার হরাইজন বা দিগন্ত সমস্যার ব্যাখ্যা দিতে পারে এই মডেল। দিগন্ত সমস্যা হলো, মহাবিশ্বকে এত লক্ষণীয়ভাবে সব দিকে সুষম দেখায় কেন। এর কারণ, মেমব্রেনটি দীর্ঘ সময় ধরে ধীরে ধীরে সাম্যাবস্থায় পৌঁছায়। কাজেই স্ফীতি তত্ত্ব যেখানে দিগন্ত সমস্যার ব্যাখ্যা করে মহাবিশ্বের হঠাৎ স্ফীতি দিয়ে, সেখানে এই মডেল দিগন্ত সমস্যার সমাধান করে বিপরীত দিক দিয়ে। অর্থাৎ মহাবিশ্ব ধীরগতিতে সাম্যাবস্থায় পৌঁছার কারণে এটা ঘটে।

(এর মানে এটাও দাঁড়ায়, হাইপারস্পেসে অন্যান্য মেমব্রেনও ভেসে বেড়ানোর সম্ভাবনা আছে, যারা হয়তো ভবিষ্যতে আমাদের সঙ্গে সংঘর্ষের মুখে পড়বে। এরপর আরেকটা বিগ স্প্যান্ট (মহাশব্দ) ঘটাবে। আমাদের মহাবিশ্ব ত্বারিত হচ্ছে—এই বাস্তবতায় অন্য আরেকটি সংঘর্ষ ঘটার সম্ভাবনাও আছে। স্টেইনহার্ড এখানে আরেকটা কথা যোগ করেছেন, ‘হয়তো মহাবিশ্বের প্রসারণের ত্বরণ এ ধরনের কোনো সংঘর্ষের পূর্বাভাস। চিন্তাটা মোটেও সুখকর নয়।’)

যেকোনো চিত্র যেটা স্ফীতির বিরাজমান চিত্রকে নাটকীয় চ্যালেঞ্জ জানায়, তা উত্তপ্ত উত্তর দিতে বাধ্য। আসলে ওয়েবসাইটে এ-বিষয়ক পেপারটি প্রকাশের এক সপ্তাহের মধ্যে এই মডেলের একটা সমালোচনা করেন আন্দ্রেই লিন্দে এবং তাঁর স্ত্রী রেনেটা ক্যালোস (তিনি নিজেও একজন স্ট্রিং থিওরিস্ট) এবং টরন্টো বিশ্ববিদ্যালয়ের লেক কফম্যান। লিন্দে এই মডেলকে সমালোচনা করেছিলেন। কারণ, দুটি মহাবিশ্বের এই সংঘর্ষের মতো যেকোনো বড় বিপর্যয়ই একটা সিঙ্গুলারিটি বা পরম বিন্দু হয়তো তৈরি করতে পারে। সেখানে তাপমাত্রা ও ঘনত্ব হবে অসীম। ‘সেটা হতে পারে একটা কৃষ্ণগহ্বরের ভেতর একটা চেয়ার ছুড়ে ফেলার মতো। সেখানে চেয়ারের কণাগুলো বাষ্পীভূত হয়ে যাবে। বলা হয়, কৃষ্ণগহ্বরটি কোনো একভাবে চেয়ারের আকারকে সংরক্ষণ করে রাখবে।’, লিন্দে প্রতিবাদ করে বলেন।

জবাবে পাল্টা গুলি ছুড়ে স্টেইনহার্ড বললেন, ‘চার মাত্রায় যেটা একটা পরম বিন্দুর মতো দেখাবে, সেটা হয় পাঁচ মাত্রায় তেমন লাগবে না…ব্রেনগুলো যখন পরস্পরের সঙ্গে একত্রে মড়মড় শব্দে মিশে যাবে, তখন পঞ্চম মাত্রা অদৃশ্য হবে সাময়িকভাবে। অবশ্য ব্রেনগুলো নিজেরা অদৃশ্য হবে না। সুতরাং ঘনত্ব ও তাপমাত্রা অসীমে যাবে না। সময়ও চলতে শুরু করবে একই সঙ্গে। অবশ্য সাধারণ আপেক্ষিকতা এখানে নীরব হয়ে গেলেও স্ট্রিং থিওরির ক্ষেত্রে তা হবে না। আর আমাদের মডেলে যে বিষয়টিকে একসময় একটা বিপর্যয় বলে মনে করা হচ্ছিল, সেটাই এখন মনে হচ্ছে নিয়ন্ত্রণযোগ্য।’

স্টেইনহার্ডের পক্ষে ছিল এম-তত্ত্বের শক্তি, যা পরম বিন্দু দূর করার জন্য পরিচিত। আসলে এ কারণে তাত্ত্বিক পদার্থবিদদের সবগুলো অসীম দূর করতে দরকার একটা মহাকর্ষের কোয়ান্টাম তত্ত্ব। তবে এই মডেলে একটা ধারণাগত দুর্বলতার কথা উল্লেখ করেছেন লিন্দে। তিনি বলেছেন, ব্রেনগুলো শুরুতে একটা সমতল, সুষম অবস্থায় থাকে। লিন্দে বলেন, ‘আপনি যদি পরিপূর্ণতা দিয়ে শুরু করেন, তাহলে কী দেখতে পাচ্ছেন তা হয়তো ব্যাখ্যা করতে পারবেন…তবু প্রশ্নটির উত্তর মিলবে না: মহাবিশ্বের শুরুটা কেন নিখুঁতভাবে হওয়া উচিত।’ জবাবে স্টেইনহার্ড বলেছেন, ‘সমতল যোগ সমতল সমান সমান সমতল।’ অন্য কথায়, আপনাকে ধরেই নিতে হবে যে মেমব্রেনগুলো সমতল হওয়ার কারণে সর্বনিম্ন শক্তি অবস্থায় শুরু হয়েছিল।

এ ব্যাপারে অ্যালান গুথের ভাবনাটা বেশ উদার। তিনি বলেন, “আমার মনে হয় না, পল এবং নীলের বিষয়গুলো প্রমাণের কাছাকাছি চলে গেছে। কিন্তু তাদের ধারণাগুলো দেখতে বেশ মূল্যবান বলেই মনে হচ্ছে।’ স্ফীতি তত্ত্বকে ব্যাখ্যা করতে স্ট্রিং তাত্ত্বিকদের তালিকা ও চ্যালেঞ্জগুলোও তিনি দেখেছেন, ‘আমার ধারণা, দীর্ঘ মেয়াদে স্ট্রিং থিওরি এবং এম-থিওরিকে স্ফীতি তত্ত্বের সঙ্গে সম্পর্কিত করা দরকার। কারণ, স্ফীতি তত্ত্ব যে কারণে ডিজাইন করা হয়েছে, সেই সমস্যার অনস্বীকার্য সমাধান। অর্থাৎ মহাবিশ্ব এত সুষম ও সমতল কেন, এই প্রশ্নের সমাধান।’ তাই তিনি এই প্রশ্নটি করেছেন : এম-তত্ত্ব কি স্ফীতির আদর্শ মডেলটি তুলে ধরতে পারে?

সবশেষে কসমোলজির আরেকটা প্রতিদ্বন্দ্বীমূলক তত্ত্ব আছে, যা স্ট্রিং থিওরি কাজে লাগায়। সেটি হলো গ্যাবরিয়েল ভেনিজিয়ানোর প্রি-বিগ ব্যাং থিওরি। সেই ১৯৬৮ সালে স্ট্রিং থিওরি শুরু করতে সহায়তা করেন এই পদার্থবিদ। তাঁর তত্ত্বমতে, মহাবিশ্বের শুরুটা হয়েছে আসলে একটা কৃষ্ণগহ্বর হিসেবে। একটা কৃষ্ণগহ্বরের ভেতরটা দেখতে কেমন, তা যদি জানতে চেষ্টা করি, তাহলে আমাদেরকে বাইরের দিকে তাকাতে হবে।

এই তত্ত্বে মহাবিশ্ব আসলে সীমাহীনভাবে পুরোনো। এর শুরু হয়েছিল বহুদূর অতীতের প্রায় শূন্য ও শীতল এক অবস্থায়। মহাকর্ষ মহাবিশ্বের পদার্থগুলোর মধ্যে গুচ্ছ তৈরি করতে শুরু করে। সেগুলো ধীরে ধীরে বিভিন্ন এলাকায় এতই ঘনীভূত হয়ে ওঠে যে একসময় কৃষ্ণগহ্বরে পরিণত হয়। প্রতিটি কৃষ্ণগহ্বরের চারদিকে ঘটনাদিগন্তও গঠিত হতে থাকে। ফলে চিরস্থায়ীভাবে ঘটনাদিগন্তের অভ্যন্তরীণ অংশগুলো আলাদা হয়ে পড়ে বাইরের অংশ থেকে। মহাকর্ষের প্রভাবে প্রতিটি ঘটনা দিগন্তের ভেতর পদার্থগুলো ক্রমে সংকুচিত হতে থাকে। কৃষ্ণগহ্বর প্ল্যাঙ্ক দৈর্ঘ্যে না পৌঁছানো পর্যন্ত চলতে থাকে এই সংকোচন।

এই বিন্দুতে এসে স্ট্রিং থিওরি আধিপত্য বিস্তার করে। স্ট্রিং থিওরি অনুযায়ী, প্ল্যাঙ্ক দৈর্ঘ্যই হলো সর্বনিম্ন দূরত্ব। কৃষ্ণগহ্বর এরপর একটা বিশাল বিস্ফোরণের দিকে যেতে থাকে, যার কারণে সৃষ্টি হয় বিগ ব্যাং বা মহাবিস্ফোরণের। এই প্রক্রিয়া নিজে নিজেই পুনরাবৃত্তি করতে পারে মহাবিশ্বজুড়ে। তাই বহুদূরে কৃষ্ণগহ্বর, এমনকি মহাবিশ্বও থাকতে পারে।

(আমাদের মহাবিশ্ব একটা কৃষ্ণগহ্বর হতে পারে—এমন ধারণা আপাতদৃষ্টে সুদূরপ্রসারী মনে হলেও বাস্তবে আসলে ততটা নয়। আমাদের মোটামুটি জানা আছে, একটা কৃষ্ণগহ্বরকে অবশ্যই চরমভাবে ঘন হতে হবে। সেই সঙ্গে তার থাকবে একটা বিপুল শক্তিশালী আর বিপর্যয়কর মহাকর্ষ ক্ষেত্র। কিন্তু সব সময়ের জন্য এটা সত্য নয়। কৃষ্ণগহ্বরের ঘটনাদিগন্ত তার ভরের সমানুপাতিক। কৃষ্ণগহ্বরের ভর যত বেশি হবে, তার ঘটনাদিগন্ত তত বড় হবে। কিন্তু একটা বড়সড় ঘটনাদিগন্তের মানে হলো, পদার্থ একটা বড় আয়তনের মধ্যে ছড়িয়ে আছে। ফলে ভর বাড়ার সঙ্গে সঙ্গে তার ঘনত্বও কমতে থাকে। আসলে একটা কৃষ্ণগহ্বরের ভর আমাদের মহাবিশ্বের মতো হলে, তার আকার হবে আমাদের মহাবিশ্বের আকারের প্রায় সমান। আবার তার ঘনত্বও হবে আমাদের মহাবিশ্বের তুলনায় বেশ কম।)

তবে বেশ কয়েকজন জ্যোতিঃপদার্থবিদ কসমোলজিতে স্ট্রিং থিওরি এবং এম-থিওরির প্রয়োগে তেমন মুগ্ধ হতে পারেন না। সান্তা ক্রুজে ক্যালিফোর্নিয়া বিশ্ববিদ্যালয়ের জোয়েল প্রিম্যাক অন্যদের তুলনায় একটু কম দয়াশীল। তিনি বলেন, ‘আমার ধারণা, এই বিষয়গুলো বেশি বেশি উৎপাদন করা বোকামি…এসব গবেষণাপত্রের ধারণা অনিবার্যভাবে পরীক্ষাযোগ্য নয়।’ প্রিম্যাক সঠিক কি না, তা একমাত্র বলতে পারে সময়। কিন্তু স্ট্রিং থিওরির গতি বেশ ত্বরান্বিত হওয়ার কারণে হয়তো এ সমস্যার একটা সমাধান শিগগিরই পাওয়া যাবে। সেটা হয়তো আসতে পারে আমাদের স্পেস স্যাটেলাইটগুলো থেকেও। নবম অধ্যায়ে দেখতে পাবো, লিসার (LISA) মতো নতুন প্রজন্মের মহাকর্ষ তরঙ্গ ডিটেক্টর ২০২০ সালের মধ্যে মহাকাশে পাঠানোর কথা। [২০৩৪ সালে পাঠানো হবে।-অনুবাদক] এর মাধ্যমে আমরা হয়তো এসব তত্ত্ব বাতিল বা যাচাই করার সক্ষমতা অর্জন করব। যেমন স্ফীতি তত্ত্ব সঠিক হলে, আদি স্ফীতি প্রক্রিয়ার কারণে সৃষ্ট বিক্ষুব্ধ মহাকর্ষ তরঙ্গ শনাক্ত করতে পারবে লিসা। ইকপাইরোটিক মহাবিশ্ব (EkPyrotic Universe) অনুমান করে, মহাবিশ্বগুলোর মধ্যে একটা ধীরগতির সংঘর্ষ হয়েছিল। তার ফলে সৃষ্টি হয়েছিল বেশ হালকা মহাকর্ষ তরঙ্গের। এসব তত্ত্ব পরীক্ষামূলকভাবে বাতিল করতে পারার কথা লিসার। অন্য কথায়, কোনো মডেলটি সঠিক তা নির্ধারণের জন্য দরকার আদি মহাবিস্ফোরণের মাধ্যমে সৃষ্ট মহাকর্ষ তরঙ্গের সংকেতাবদ্ধ উপাত্ত। লিসা হয়তো প্রথমবারের মতো স্ফীতি, স্ট্রিং থিওরি এবং এম-থিওরির সম্পর্কিত নির্ভরযোগ্য পরীক্ষামূলক ফলাফল দিতে পারবে।

মিনি ব্ল্যাকহোল

স্ট্রিং থিওরি আসলে গোটা মহাবিশ্বের একটা তত্ত্ব। তাই একে সরাসরি পরীক্ষা করে দেখার জন্য পরীক্ষাগারে একটা মহাবিশ্ব বানানো প্রয়োজন (নবম অধ্যায়ে দেখুন)। স্বাভাবিকভাবে আশা করা যায়, মহাকর্ষ থেকে কোয়ান্টাম প্রভাবগুলো ঘটবে প্ল্যাঙ্ক শক্তি পর্যায়ে। এই প্ল্যাঙ্ক শক্তি আমাদের সবচেয়ে শক্তিশালী পার্টিকেল অ্যাকসিলেটর বা কণাত্বরক যন্ত্রের চেয়েও কোয়াড্রিলিয়ন গুণ বেশি শক্তিশালী। এ কারণে স্ট্রিংয়ের সরাসরি পরীক্ষা করা অসম্ভব হয়ে দাঁড়ায়। কিন্তু সমান্তরাল মহাবিশ্বের অস্তিত্ব যদি আমাদের মহাবিশ্ব থেকে মাত্র এক মিলিমিটারের কম দূরত্বে সত্যিই থাকে, তাহলে যে পর্যায়ে শক্তি একীভূত হয় এবং কোয়ান্টাম প্রভাব ঘটে, সেগুলো হয়তো অনেক নিচেই ঘটবে। অর্থাৎ আমাদের পরের প্রজন্মের কণা ত্বরকযন্ত্র, যেমন লার্জ হ্যাড্রন কলায়ডারে (এলএইচসি) এ পর্যায়ে পৌঁছানো সম্ভব হতে পারে। ফলে কৃষ্ণগহ্বর পদার্থবিজ্ঞানের দিকে আগ্রহও বাড়িয়ে তুলেছে এটা। বিশেষ করে মিনি ব্ল্যাকহোলের প্রতি। মিনি কৃষ্ণগহ্বর এমন আচরণ করে যেন সেগুলো কোনো অতিপারমাণবিক কণা। স্ট্রিং থিওরির কিছু ভবিষ্যদ্বাণী পরীক্ষা করে দেখতে মিনি কৃষ্ণগহ্বরকে একটা ‘গবেষণাগার’ বলা চলে। এলএইচসিতে এদের তৈরির সম্ভাবনার ব্যাপারে বেশ উত্তেজিত পদার্থবিদেরা। (একটা ইলেকট্রনের তুলনায় মিনি ব্ল্যাকহোল খুব ছোট। তাই তারা পৃথিবীকে গিলে খাওয়ার কোনো ঝুঁকিও নেই। মহাজাগতিক রশ্মি পৃথিবীতে নিয়মিত আঘাত হানে, যার কোনো ক্ষতিকর প্রভাব নেই। মহাজাগতিক রশ্মির শক্তির পরিমাণ এসব মিনি ব্ল্যাকহোলের শক্তির চেয়েও বেশি।)

একে দেখতে যতই বৈপ্লবিক মনে হোক না কেন, অতিপারমাণবিক কণার ছদ্মবেশে একটা কৃষ্ণগহ্বরের ধারণা বেশ পুরোনো। ১৯৩৫ সালে এর প্রবর্তন করেন স্বয়ং আইনস্টাইন। আইনস্টাইনের মতে, একটা ইউনিফায়েড ফিল্ড থিওরি অবশ্যই আছে। সে তত্ত্বটা অতিপারমাণবিক কণা দিয়ে তৈরি পদার্থকে স্থান-কালের নকশায় কোনো ধরনের বিকৃতি হিসেবে ব্যাখ্যা করবে। তাঁর কাছে ইলেকট্রনের মতো অতিপারমাণবিক কণারা ছিল, বিকৃত স্থানে ফাঁস বা ওয়ার্মহোল, যাকে দূর থেকে একটা কণার মতো দেখায়। নাথান রোজেনের সঙ্গে আইনস্টাইন এই ধারণা চালু করেন যে, একটা ইলেকট্রন আসলে একটা মিনি কৃষ্ণগহ্বরের ছদ্মবেশ হতে পারে। এই উপায়ে নিজের ইউনিফায়েড ফিল্ড থিওরির সঙ্গে বস্তুকে সম্পর্কিত করতে চেষ্টা করতে চেয়েছিলেন তিনি। এর মাধ্যমে অতিপারমাণবিক কণাকে বিশুদ্ধ জ্যামিতিতে আনতে পারেন।

মিনি ব্ল্যাকহোলের কথা আবারও চালু করেন স্টিফেন হকিং। তিনি প্রমাণ করেন, কৃষ্ণগহ্বর অবশ্যই বাষ্পীভূত হয়ে যায় এবং শক্তির ম্লান আভা নিঃসরণ করে। অনেক অনেক যুগ পরে একটা কৃষ্ণগহ্বর এত বেশি শক্তি নিঃসরণ করে যে তা ধীরে ধীরে সংকুচিত হতে থাকে। একসময় তা অতিপারমাণবিক কণার সমান হয়ে দাঁড়ায়।

এখন এই মিনি ব্ল্যাকহোলের ধারণা নতুন করে পরিচয় করে দিয়েছে স্ট্রিং থিওরি। মনে আছে নিশ্চয়ই, বিপুল পরিমাণ পদার্থ যখন তার শোয়ার্জশিল্ড ব্যাসার্ধে সংকুচিত হয়, তখন কৃষ্ণগহ্বর গঠিত হয়। ভর ও শক্তিকে পরস্পরের মধ্যে রূপান্তর করা যায়। তাই শক্তিকে সংকুচিত করেও কৃষ্ণগহ্বর গঠিত হওয়া সম্ভব। দুটি প্রোটনকে ১৪ ট্রিলিয়ন ইলেকট্রন ভোল্ট শক্তিতে ভেঙে অবশিষ্টাংশ থেকে এলএইচসি মিনি ব্ল্যাকহোল তৈরি করতে পারবে কি না, তা নিয়ে বেশ আগ্রহ দেখা দিয়েছে। এসব কৃষ্ণগহ্বর হবে খুব ছোট। এদের ওজন হয়তো হবে একটা ইলেকট্রনের এক হাজার ভাগের মাত্র এক ভাগ। আর তার স্থায়িত্ব হবে মাত্র ১০^-২৩ সেকেন্ড। কিন্তু এলএইচসির মাধ্যমে তৈরি অতিপারমাণবিক কণাদের গতিপথ অনুসরণের মাধ্যমে তাদের স্পষ্টভাবে দেখা সম্ভব।

পদার্থবিদেরা এটাও আশা করেন, বাইরের মহাকাশ থেকে আসা কসমিক রে বা মহাজাগতিক রশ্মিতে হয়তো মিনি কৃষ্ণগহ্বর থাকতে পারে। আর্জেন্টিনার পিয়েরে আগার কসমিক রে অবজারভেটরি এতই সংবেদী যে কিছু বড় ধরনের কসমিক রে বিস্ফোরণ শনাক্ত করতে পারে এটা। সেগুলো বিজ্ঞানের ইতিহাসে এখন পর্যন্ত একটা রেকর্ড বলা যায়। আশা করা হচ্ছে, মিনি কৃষ্ণগহ্বর প্রাকৃতিকভাবে দেখা যাবে মহাজাগতিক রশ্মিতে। এই রশ্মি পৃথিবীর বায়ুমণ্ডলের ওপরের স্তরে আঘাত হানলে বিশেষ ধরনের বিকিরণের ধারাবর্ষণ করবে। এক হিসেবে দেখা গেছে, হয়তো মিনি কৃষ্ণগহ্বরের কারণে সৃষ্ট ১০টি মহাজাগতিক রশ্মির ধারাবর্ষণ প্রতিবছর দেখতে পারবে আগার কসমিক রে ডিটেক্টর।

সুইজারল্যান্ডের এলএইচসি কিংবা আর্জেন্টিনার আগার কসমিক রে ডিটেক্টরে হয়তো এই দশকে কোনো মিনি কৃষ্ণগহ্বরের শনাক্ত হতে পারে। এর ফলে মিলবে সমান্তরাল মহাবিশ্বের অস্তিত্বের ভালো একটা প্রমাণ। অবশ্যই সেটা স্ট্রিং থিওরির যথার্থতা চূড়ান্তভাবে প্রমাণ করবে। তবে গোটা পদার্থবিজ্ঞান সম্প্রদায়কে বোঝাতে সক্ষম হবে যে স্ট্রিং থিওরি সব ধরনের পরীক্ষামূলক ফলাফলের সঙ্গে মানানসই এবং সঠিক পথেই রয়েছে স্ট্রিং থিওরি।

কৃষ্ণগহ্বর ও ইনফরমেশন প্যারাডক্স

কৃষ্ণগহ্বরবিষয়ক পদার্থবিজ্ঞানের আরও কিছু বিষয়, যেমন ইনফরমেশন প্যারাডক্সের দিকেও হয়তো আলোকপাত করবে স্ট্রিং থিওরি। নিশ্চয়ই মনে আছে, কৃষ্ণগহ্বর পুরোপুরি কালো নয়, বরং টানেলিংয়ের মাধ্যমে তা অল্প পরিমাণে বিকিরণ নিঃসরণ করে। কোয়ান্টাম তত্ত্বের কারণে সব সময় একটা অল্প সম্ভাবনা থাকে যে কৃষ্ণগহ্বরের মহাকর্ষের বজ্র আঁটুনি থেকে বিকিরণ বেরিয়ে আসতে পারবে। এর ফলেই একটা কৃষ্ণগহ্বর থেকে ধীরে ধীরে বিকিরণ চুইয়ে আসতে শুরু করে। একেই বলা হয় হকিং রেডিয়েশন বা হকিং বিকিরণ।

এই বিকিরণ একটা তাপমাত্রার সঙ্গে সম্পর্কিত (যা কৃষ্ণগহ্বরের ঘটনাদিগন্তের পৃষ্ঠতলের ক্ষেত্রফলের সমানুপাতিক)। এ সমীকরণের এক সাধারণ বিবৃতি দিয়েছেন হকিং। তবে এ ফলাফলের যথার্থ পথ ব্যাখ্যার জন্য পরিসংখ্যানিক বলবিদ্যার পরিপূর্ণ শক্তি ব্যবহার করার দরকার হয় (কৃষ্ণগহ্বরের কোয়ান্টাম দশা গণনার ওপর ভিত্তি করে)। সাধারণত পরিসংখ্যানিক বলবিদ্যা গণনা করতে হয়, একটা পরমাণু বা অণু কতটা অবস্থা বা দশা দখল করতে পারে, তার সংখ্যা গুনে। কিন্তু একটা কৃষ্ণগহ্বরের কোয়ান্টাম অবস্থা কীভাবে গণনা করা হয়? আইনস্টাইনের তত্ত্বে, কৃষ্ণগহ্বর নিখুঁতভাবে মসৃণ। তাই তাদের কোয়ান্টাম দশা গণনা বেশ সমস্যাসংকুল।

স্ট্রিং তাত্ত্বিকেরা এই ফাঁকটি পূর্ণ করার ব্যাপারে বেশ উদ্বিগ্ন। সে জন্য এম-তত্ত্ব ব্যবহার করে একটা কৃষ্ণগহ্বর বিশ্লেষণের সিদ্ধান্ত নেন হার্ভার্ডের অ্যান্ড্রিউ স্ট্রোমনিগার এবং কামরাম ভাফা। কৃষ্ণগহ্বর নিয়ে কাজ করা খুব কঠিন। তাই তারা ভিন্ন একটা পদ্ধতি অবলম্বন করেন। সেই সঙ্গে কৌশলী এক প্রশ্নও তোলেন : কোনো কৃষ্ণগহ্বরের দ্বৈততা কী হবে? (মনে করা যাক, একটা ইলেকট্রন চুম্বকীয় এক মেরুতে দ্বৈত বা দ্বিগুণ। যেমন একক উত্তর মেরুতে। তাই কোনো দুর্বল বৈদ্যুতিক ক্ষেত্রে একটা ইলেকট্রনকে পরীক্ষার মাধ্যমে (যেটা করা বেশ সহজ) আমরা অনেক অনেক জটিল পরীক্ষা বিশ্লেষণ করতে পারি : খুব বড় কোনো চুম্বকীয় ক্ষেত্রে একটা মনোপল বা এক মেরু রেখে।) আশা ছিল, কৃষ্ণগহ্বরের তুলনায় তার দ্বৈততাকে সহজে বিশ্লেষণ করা যাবে। কিন্তু তাদের ফলাফল চূড়ান্তভাবে একই হবে। ধারাবাহিক গাণিতিক কৌশলের মাধ্যমে স্ট্রোমিনগার এবং ভাফা দেখাতে সক্ষম হন, কৃষ্ণগহ্বরটি একটা ব্রেন ও পাঁচ-ব্রেনের একটা গুচ্ছের দ্বৈত ছিল। ফলে উদ্বেগ নিরসন হলো ব্যাপকভাবে। কারণ, এসব ব্রেনের কোয়ান্টাম দশা গণনার বিষয়টি জানা ছিল। স্ট্রোমিনগার এবং ভাষা এরপর কোয়ান্টাম দশার সংখ্যা গণনা করে দেখতে পান, উত্তরটি নিখুঁতভাবে হকিংয়ের ফলাফলটি নতুন করে তৈরি করেছে।

এটা ছিল সুসংবাদের খানিকমাত্র। মাঝেমধ্যে বাস্তব জগতের সঙ্গে সংযোগ না তৈরি করার কারণে স্ট্রিং থিওরিকে বেশ উদ্ভট বলে মনে হয়। কিন্তু কৃষ্ণগহ্বর তাপগতিবিদ্যার জন্য সম্ভবত সবচেয়ে অভিজাত সমাধান পাওয়া যায় এখান থেকেই

এখন কৃষ্ণগহ্বরসংক্রান্ত সবচেয়ে জটিল সমস্যাটি সমাধানের চেষ্টা করছেন স্ট্রিং তাত্ত্বিক পদার্থবিদেরা। সেটা হলো ইনফরমেশন প্যারাডক্স। হকিং যুক্তি দেখান, কৃষ্ণগহ্বরে কিছু ছুড়ে ফেলা হলে এতে থাকা সব তথ্য হারিয়ে বা ধ্বংস হয়ে যাবে চিরকালের জন্য। তা আর কখনো ফিরে পাওয়া যাবে না। (নিখুঁত অপরাধের জন্য চতুর একটা কৌশল হতে পারে এটা। কোনো অপরাধী নিজের সব অপরাধমূলক প্রমাণ নষ্ট করতে একটা কৃষ্ণগহ্বর কাজে লাগাতে পারে।) দূর থেকে একটা কৃষ্ণগহ্বরের যেসব প্যারামিটার মাপা যায়, সেগুলো হলো ভর, স্পিন ও চার্জ। কৃষ্ণগহ্বরের মধ্যে যেটাই ফেলা হোক, তার সমস্ত তথ্য হারিয়ে যাবে। (এ জন্য বলা হয় ‘কৃষ্ণগহ্বরের কোনো লোম নেই’ বা কৃষ্ণগহ্বর লোমশূন্য। সোজা কথায়, শুধু এই তিন প্যারামিটার ছাড়া এখানে সব তথ্য, সব লোম হারিয়ে যায়।)

আমাদের মহাবিশ্ব থেকে তথ্য হারিয়ে যাওয়াকে মনে হয় আইনস্টাইনের তত্ত্বের অনিবার্য পরিণতি। কিন্তু কোয়ান্টাম বলবিদ্যার নীতি লঙ্ঘন সেটা। কোয়ান্টাম বলবিদ্যামতে, তথ্য কখনো হারিয়ে বা গায়েব হয়ে যেতে পারে না। এমনকি কোনো কৃষ্ণগহ্বরের গলা দিয়ে আসল বস্তুটি নিচের দিকে নেমে গেলেও মহাবিশ্বের কোনো এক জায়গায় তথ্যটি অবশ্যই ভাসমান থাকতেও পারে।

‘অধিকাংশ পদার্থবিদ বিশ্বাস করতে চান যে তথ্য আসলে ধ্বংস হয়ে যায় না।’, হকিং লিখেছেন, ‘এর মাধ্যমে বিশ্ব হয়তো নিরাপদ ও অনুমানযোগ্য হয়ে উঠবে। কিন্তু আমার বিশ্বাস, আইনস্টাইনের সাধারণ আপেক্ষিক তত্ত্ব গুরুত্বের সঙ্গে নিলে, এটাই অনুমোদন করতে হবে যে স্থান-কাল নিজের সঙ্গে ফাঁস তৈরি করবে। তথ্যগুলো হারিয়ে যাবে এই ভাঁজের মধ্যে। তথ্য আসলে ধ্বংস হয় নাকি হয় না—তা নির্ধারণ করাই এখন তাত্ত্বিক পদার্থবিজ্ঞানের অন্যতম প্রধান প্ৰশ্ন।’

এই প্যারাডক্সের ফাঁকগুলো বেশির ভাগ স্ট্রিং তাত্ত্বিকের বিরুদ্ধে ব্যবহার করেন হকিং, কিন্তু প্যারাডক্সটির সমাধান এখনো হয়নি। তবে স্ট্রিং তাত্ত্বিকদের মধ্যে বাজি ধরার কারণে শেষ পর্যন্ত আমরা খুঁজে পাব যে হারিয়ে যাওয়া তথ্যগুলো আসলে কোথায় যায়। (যেমন আপনি যদি কৃষ্ণগহ্বরের ভেতর একটা বই ছুড়ে ফেলেন, তাহলে অনুমান করা যায় যে বইতে থাকা তত্ত্বগুলো ধীরে ধীরে আমাদের মহাবিশ্বে ফিরে আসবে। অর্থাৎ তা ফিরে আসবে বাষ্পীভূত হওয়া কোনো কৃষ্ণগহ্বর থেকে হকিং বিকিরণের ছোট কম্পন রূপে। কিংবা সেগুলো হয়তো কৃষ্ণগহ্বরের অন্য প্রান্তের কোনো হোয়াইট হোল বা শ্বেতগহ্বরে নতুন করে উদয় হবে।) এ কারণে আমি ব্যক্তিগতভাবে মনে করি, কৃষ্ণগহ্বরের অদৃশ্য হয়ে যাওয়া তথ্যের ভাগ্যে কী ঘটে—তা স্ট্রিং থিওরি ব্যবহার করে কেউ যখন গণনা করবে, তখন দেখা যাবে যে তথ্য আসলে ধ্বংস হয় না, বরং নতুন করে সূক্ষ্মভাবে অন্য কোথায় আবির্ভূত হয়।

২০০৪ সালে সবাইকে অবাক করে দিয়ে টিভি ক্যামেরার সামনে হকিং ঘোষণা করেন, ইনফরমেশন সমস্যার ব্যাপারে এতকাল আসলে ভুল করেছিলেন তিনি। সেটি নিউইয়র্ক টাইমস-এর প্রথম পাতায় বেশ গুরুত্ব দিয়ে ছাপা হয়। (৩০ বছর আগে, তিনি অন্য পদার্থবিদদের সঙ্গে বাজি ধরেছিলেন। বাজির বিষয়বস্তু ছিল—তথ্য কখনো কোনো কৃষ্ণগহ্বর চুইয়ে বাইরে যেতে পারবে না। এই বাজিতে হেরে বিজয়ীকে একটা এনসাইক্লোপিডিয়া উপহার দেন তিনি, যেখান থেকে তথ্য সহজেই উদ্ধার করা সম্ভব।) তাঁর করা সহজতর কিছু গণনা আবারও করে দেখেন তিনি। এরপর সিদ্ধান্তে আসেন, কোনো বস্তু, যেমন একটা বই যদি কৃষ্ণগহ্বরে পড়ে যায়, তাহলে সেটা হয়তো তার নিঃসরণের বিকিরণ ক্ষেত্রকে বিঘ্নিত করে। ফলে তথ্য চুইয়ে মহাবিশ্বে ফেরত আসতে পারে। বইয়ের মধ্যে থাকা তথ্য কৃষ্ণগহ্বর থেকে ধীরে ধীরে বেরিয়ে বিকিরণে সংকেতাবদ্ধ থাকবে। কিন্তু তা থাকবে বিকৃত বা জটিল রূপে।

অন্যদিকে এ কারণে অধিকাংশ কোয়ান্টাম পদার্থবিদের সঙ্গে এখন একই সারিতে এসে দাঁড়িয়েছেন হকিং। এসব পদার্থবিদ বিশ্বাস করেন, তথ্য কখনো ধ্বংস হয়ে যেতে পারে না। কিন্তু এতে একটা প্রশ্ন ওঠে : তথ্য কি তাহলে অন্য কোনো সমান্তরাল মহাবিশ্ব চলে যেতে পারে? আপাতদৃষ্টে মনে হয়, তথ্য যে ওয়ার্মহোলের ভেতর দিয়ে কোনো সমান্তরাল মহাবিশ্বে চলে যেতে পারে—এ ধারণার প্রতি তাঁর ফলাফল সন্দেহ প্রকাশ করে। তবে এ বিষয়ে

এটাই যে শেষ কথা, তা-ও কেউ বিশ্বাস করে না। স্ট্রিং থিওরি পুরোপুরি বিকশিত না হওয়া পর্যন্ত, কিংবা কোয়ান্টাম মহাকর্ষীয় গণনা সম্পূর্ণ না হওয়া পর্যন্ত কেউই বিশ্বাস করবে না যে ইনফরমেশন প্যারাডক্স পুরোপুরি সমাধান করা সম্ভব হয়েছে।

হলোগ্রাফিক মহাবিশ্ব

সবশেষে বলতে হয়, এর চেয়েও রহস্যময় একটা ভবিষ্যদ্বাণী করে এম-তত্ত্ব। কিন্তু মজার ব্যাপার হলো, সে ভবিষ্যদ্বাণী এখনো বুঝে ওঠা সম্ভব হয়নি। এর হয়তো গভীর কোনো ভৌত ও দার্শনিক পরিণতি থাকতে পারে। এই ফলাফল আমাদের প্রশ্ন করতে বাধ্য করে: মহাবিশ্ব কি তাহলে কোনো হলোগ্রাম? কোথাও কি কোনো ছায়া মহাবিশ্ব আছে, যেখানে আমাদের দেহগুলো একটা সংকুচিত দ্বিমাত্রিক অবস্থায় বর্তমান? এটা থেকে আবার আরেকটা বিব্রতকর প্রশ্নও উঠে আসে : মহাবিশ্ব কি কোনো কম্পিউটার প্রোগ্রাম? মহাবিশ্বকে কি কোনো সিডিতে রাখা সম্ভব, আমাদের অবসর সময়ে যা চালানো যায়?

এখন ক্রেডিট কার্ডে, শিশুদের মিউজিয়ামে ও অ্যামিউজমেন্ট পার্কেও হলোগ্রাম দেখা যায়। এগুলো চোখে পড়ার মতো। কারণ, এতে একটা সম্পূর্ণ ত্রিমাত্রিক ছবি দ্বিমাত্রিক তুলে ধরে রাখা যায়। সাধারণত কোনো ফটোগ্রাফের দিকে অপলক তাকিয়ে মাথাটা অন্যদিকে ঘোরালে ফটোগ্রাফের ছবির কোনো পরিবর্তন হয় না। কিন্তু হলোগ্রাম এর চেয়ে আলাদা। একটা হলোগ্রাফিক ছবির দিকে স্থির চোখে তাকিয়ে আপনার মাথা এদিক-ওদিক ঘোরালে দেখা যাবে ছবিটিও বদলে যাচ্ছে। মনে হবে যেন, আপনি ছবিটির দিকে তাকিয়ে আছেন কোনো জানালা কিংবা কিহোলের ভেতর দিয়ে। (হলোগ্রাম হয়তো ভবিষ্যতে ত্রিমাত্রিক টিভি ও মুভিতে জায়গা করে নিতে পারবে। ভবিষ্যতে আমরা হয়তো বসার ঘরে আয়েশ করে বসে দেয়ালের স্ক্রিনের দিকে তাকাব। সেখান থেকে হয়তো দূরের কোনো জায়গা থেকে আসা সম্পূর্ণ ত্রিমাত্রিক ছবি দেখা যাবে। তখন মনে হবে, টিভির ওয়াল স্ক্রিনটা আসলে একটা জানালা। আর তার ভেতর দিয়ে অনায়াসে উঁকি দেওয়া যায় নতুন নতুন দৃশ্যপটে। আবার দেয়ালের স্ক্রিনের আকৃতি যদি বড় সিলিন্ডারের মতো হয়, যা বসার ঘরের মাঝখানে বসানো থাকবে, তাহলে দেখে মনে হবে, আমরা নতুন কোনো বিশ্বের দিকে যাচ্ছি। যেদিকেই তাকাব, সেদিকেই নতুন বাস্তবতার ত্রিমাত্রিক ছবি দেখতে পাব। তখন আর বাস্তব বস্তু থেকে সহজে আলাদা করা যাবে না তাকে। )

সংক্ষেপে হলোগ্রাম হলো, একটা ত্রিমাত্রিক ছবি পুনরায় তৈরি করতে প্রয়োজনীয় সব তথ্য সংকেতাবদ্ধ করে রাখে দ্বিমাত্রিক তলের হলোগ্রাম। (ল্যাবরেটরিতে হলোগ্রাম তৈরি করা হয় একটা সেনসিটিভ ফটোগ্রাফিক প্লেটের ওপর লেজার রশ্মির তীব্র আলো ফেলে। এখানে লেজার রশ্মির সঙ্গে ব্যতিচার করা হয় আদি উৎস থেকে আসা আলোকে। দুটি উৎসের আলোর এই ব্যতিচারের ফলে এমন এক ব্যতিচার প্যাটার্ন তৈরি হয়, যা দ্বিমাত্রিক তলের ওপর ছবিটি বেশ ‘জমে’ ওঠে।)

খোদ মহাবিশ্বের ক্ষেত্রেও এটা হয়তো ব্যবহার করা চলে বলে অনুমান করেন অনেক কসমোলজিস্ট। সোজা কথায়, তাঁদের ভাষ্য, আমরা হয়তো একটা হলোগ্রামের ভেতর বসবাস করছি। এই অদ্ভুত সন্দেহটা দানা বেঁধেছিল কৃষ্ণগহ্বরের পদার্থবিজ্ঞান থেকে। বেকেস্টাইন এবং হকিং অনুমান করেন, একটা কৃষ্ণগহ্বরে থাকা সর্বমোট তথ্যের পরিমাণ তার ঘটনাদিগন্তের (যা আসলে গোলকীয়) পৃষ্ঠতলের ক্ষেত্রফলের সমানুপাতিক। এটা অদ্ভুত এক ফলাফল। কারণ, সাধারণত তথ্য যে বস্তুতে সংরক্ষিত হয়, তাতে তথ্যের পরিমাণ বস্তুটির আয়তনের সমানুপাতিক। যেমন একটা বইয়ের ভেতরের তথ্যের পরিমাণ বইটির আকারের সমানুপাতিক হয়, বইটির মলাটের পৃষ্ঠতলের ক্ষেত্রফল নয়। এটা সহজাতভাবে জানি, যখন আমরা বলি কোনো বই তার মলাট দেখে বিচার করি না। কিন্তু অন্তর্দৃষ্টি কৃষ্ণগহ্বরের ক্ষেত্রে এসে ব্যর্থ হয়। কারণ, একটা কৃষ্ণগহ্বরের মলাট (ঘটনাদিগন্ত) দেখে তাকে পুরোপুরি বিচার করা যায়।

আমরা হয়তো এই আজগুবি হাইপোথিসিস বাতিলও করতে পারি। কারণ, কৃষ্ণগহ্বরের ভেতর অদ্ভুত কিছু অস্বাভাবিকতা থাকে, যা সাধারণ অন্তর্দৃষ্টিকে গুঁড়িয়ে দেয়। তবে এই ফলাফলটি এম-তত্ত্বে প্রয়োগ করা যায়, যেটা গোটা মহাবিশ্ব সম্পর্কে আমাদের সবচেয়ে ভালো বর্ণনাটি দিতে পারে। ১৯৯৭ সালে প্রিন্সটনের ইনস্টিটিউট ফর অ্যাডভান্সড স্টাডির জোয়ান ম্যালডেসেনা দেখান, নতুন ধরনের হলোগ্রাফিক মহাবিশ্বের ইঙ্গিত করে স্ট্রিং থিওরি। এতে বেশ চাঞ্চল্যের সৃষ্টি হয় সে সময়।

একটা পাঁচ-মাত্রিক অ্যান্টি-ডি সিটার মহাবিশ্ব নিয়ে শুরু করেন তিনি। স্ট্রিং থিওরি এবং সুপারগ্র্যাভিটি তত্ত্বে এমন মহাবিশ্বের উপস্থিতি প্রায়ই দেখা যায়। একটা ডি সিটার মহাবিশ্ব হলো এমন একটা কিছু, যার একটা ধনাত্মক মহাজাগতিক ধ্রুবক আছে। মহাবিশ্বের ত্বরণ সৃষ্টি করে এই ধ্রুবক। (আমাদের মহাবিশ্ব বর্তমানে একটা ডি সিটার মহাবিশ্বের সবচেয়ে সেরা প্রতিনিধিত্ব করছে। এর একটা মহাজাগতিক ধ্রুবক ছায়াপথগুলোকে দ্রুত থেকে দ্রুতবেগে দূরে সরিয়ে দিচ্ছে। আর একটা অ্যান্টি-ডি সিটার মহাবিশ্বের মহাজাগতিক ধ্রুবক হলো ঋণাত্মক। কাজেই তা কেন্দ্রীভূত করতে পারে।) ম্যালডাসেনা দেখিয়েছেন, এই পাঁচ-মাত্রিক মহাবিশ্বের মাঝে একটা দ্বৈততা আছে। তার সীমানা একটা চার-মাত্রিক মহাবিশ্ব। অবাক ব্যাপার হচ্ছে, এই পাঁচ-মাত্রিক স্থানে বসবাসরত যেকোনো জীব গাণিতিকভাবে এই চার-মাত্রিক স্থানে বাস করা জীবের সমতুল্য হবে। তাদের আলাদা করার কোনো উপায় নেই।

স্থূল উপমা হিসেবে গোল্ডফিশ রাখার একটা বাটির মধ্যে গুটিকয়েক মাছের সাঁতার কাটার কথা ভাবুন। এই মাছেরা মনে করে, তাদের বাটিটা বাস্তবতার সঙ্গে সম্পর্কিত। এখন এসব মাছের একটা দ্বিমাত্রিক হলোগ্রাফিক ছবির কথা কল্পনা করুন, যা মাছের বাটির পৃষ্ঠতলে প্রক্ষেপ করা হচ্ছে। এই ছবিতে আসল মাছেদের নিখুঁত প্রতিলিপি আছে, ব্যতিক্রম শুধু মাছগুলো সমতলীয়। মাছের বাটিতে মাছ যেকোনো নড়াচড়া করলে তা সমতল ছবির মাধ্যমে মাছের বাটির পৃষ্ঠতলে প্রতিফলিত হবে। বাটিতে সাঁতার কাটা এবং বাটির পৃষ্ঠতলে থাকা সমতলীয় উভয় মাছেরা মনে করবে, তারা আসলে বাস্তব মাছ। আর অন্যটাকে মনে করবে বিভ্রান্তি। উভয় মাছই জীবন্ত এবং তারা প্রকৃত মাছের মতো আচরণ করবে। কিন্তু কোন বর্ণনাটি সঠিক? আসলে দুটোই সঠিক। কারণ, গাণিতিকভাবে তারা সমতুল্য। আবার তাদের আলাদা করাও যায় না।

স্ট্রিং তাত্ত্বিকদের একটা বিষয় বেশ উত্তেজিত করেছিল। সেটা হলো পাঁচ মাত্রিক অ্যান্টি-ডি সিটার স্পেস গণনা করা তুলনামূলক সহজ, যেখানে চার- মাত্রিক ক্ষেত্র তত্ত্বগুলোর নাগাল পাওয়া খুব কঠিন। (এমনকি কয়েক দশকের কঠোর পরিশ্রমের পর আজও আমাদের সবচেয়ে শক্তিশালী কম্পিউটার চার- মাত্রিক কোয়ান্টাম মডেলের সমাধান করে প্রোটন আর নিউট্রনের ভর নির্ণয় করতে পারেনি। অবশ্য এত দিনে কোয়ার্কের সমীকরণগুলো বেশ ভালোভাবে বোঝা গেছে। কিন্তু তাদের চার মাত্রায় সমাধান করে প্রোটন আর নিউট্রনের ধর্মে নিয়ে আসা আগের ভাবনার চেয়েও অনেক কঠিন বলে প্রমাণিত হয়েছে।) এই অদ্ভুত দ্বৈততা ব্যবহার করে প্রোটন ও নিউট্রনের ভর এবং তাদের ধর্ম নির্ণয় এখন একটা প্রধান লক্ষ্য হয়ে দাঁড়িয়েছে।

এই হলোগ্রাফিক ডুয়ালিটি বা দ্বৈততার হয়তো ব্যবহারিক প্রয়োগ থাকতে পারে। যেমন কৃষ্ণগহ্বরবিষয়ক পদার্থবিজ্ঞানে ইনফরমেশন প্যারাডক্স সমাধান করা। কৃষ্ণগহ্বরে কোনো বস্তু ছুড়ে দিলে তথ্য হারিয়ে যায় না—চার মাত্রায় তা প্রমাণ করা খুব কঠিন। কিন্তু এ ধরনের কোনো স্থান একটা পাঁচ- মাত্রিক বিশ্বের দ্বৈতও হতে পারে। আর সেখানে তথ্য হয়তো কখনোই হারায় না। আশার কথা হলো, চার মাত্রাতে যেসব সমস্যা সহজে বশ করা যায় না (যেমন তথ্য সমস্যার মতো কোয়ার্ক মডেলের ভর ও অন্য বিষয়গুলো), সেগুলো হয়তো একসময় পাঁচ মাত্রায় সমাধান করা যাবে। কারণ, এখানে গণিত তুলনামূলকভাবে অনেক সরল। তাই একটা সম্ভাবনা সব সময় থাকে যে এই উপমাটি আসলে বাস্তব জগতের একটা প্রতিফলন। অর্থাৎ আমাদের বসবাস আসলে একটা হলোগ্রামে।

মহাবিশ্ব কি কোনো কম্পিউটার প্রোগ্রাম

আমরা আগেই দেখেছি, জন হুইলার বিশ্বাস করতেন, সব ভৌত বাস্তবতাকে বিশুদ্ধ তথ্যে নামিয়ে আনা সম্ভব। একটা প্রশ্ন করে বেকেস্টাইন কৃষ্ণগহ্বরের তথ্যের ধারণাটি আরও এক ধাপ এগিয়ে নিয়ে অজানা, অনাবিষ্কৃত এক সাগরে নিয়ে ফেলেন। তাঁর প্রশ্নটি ছিল : মহাবিশ্ব কি আদৌ কোনো কম্পিউটার প্রোগ্রাম? আমরা কোনো মহাজাগতিক সিডিতে থাকা শুধু কোনো বিট?

আমরা কোনো কম্পিউটার প্রোগ্রামে বসবাস করি কি না—সেই প্রশ্নটি রুপালি পর্দায় চমৎকারভাবে তুলে আনা হয়েছে দ্য ম্যাট্রিকস মুভিতে। সেখানে সব ভৌত বাস্তবতাকে একটা কম্পিউটার প্রোগ্রামের ভেতর নিয়ে আসে এলিয়েনরা। কোটি কোটি মানুষ ভাবতে থাকে, তারা স্বাভাবিকভাবে তাদের দৈনন্দিন জীবন যাপন করছে। কিন্তু মানুষগুলো ঘুণাক্ষরে জানতেও পারে না, সবই আসলে একটা কম্পিউটারনিয়ন্ত্রিত ফ্যান্টাসি। তাদের সত্যিকার দেহকে ঘুম পাড়িয়ে রাখা হয়েছে একটা পড়ের ভেতর। সেখান থেকে মানুষগুলোকে শক্তির উৎস হিসেবে ব্যবহার করে এলিয়েনরা

এই মুভিতে দেখা যায়, সেখানে ছোট ছোট কম্পিউটার প্রোগ্রামও চালানো সম্ভব। সেগুলো কৃত্রিমভাবে ছোট ছোট বাস্তবতা তৈরি করতে পারবে। কেউ যদি একজন কুংফু মাস্টার কিংবা হেলিকপ্টারের পাইলট হতে চায়, তাহলে কম্পিউটারে একটা সিডি ঢুকিয়ে দিলেই হবে। ব্যস, তাতে প্রোগ্রামটা মস্তিষ্কে ঢুকে যাবে। তারপর স্রেফ ভেল্কিবাজির মতো চোখের পলকে শিখে ফেলা যাবে ওই সব জটিল দক্ষতা। সিডিটি চলার সময় পুরোপুরি নতুন এক উপবাস্তবতা তৈরি হয়। কিন্তু এখানেও একটা প্রশ্ন ওঠে, যেটা বেশ উদ্বেগজনক : বাস্তবতার সবকিছুই কি একটা সিডিতে রাখা সম্ভব? কোটি কোটি ঘুমন্ত মানুষের বাস্তবতা জাগিয়ে তুলতে কম্পিউটারের যে পরিমাণ শক্তির দরকার, তা এককথায় অকল্পনীয়। কিন্তু তাত্ত্বিকভাবে : গোটা মহাবিশ্ব কি সসীম কম্পিউটার প্রোগ্রামে ডিজিটালাইজড করা সম্ভব?

এই প্রশ্নের শিকড় খুঁজতে গেলে ফিরে যেতে হবে নিউটনের গতি সূত্রের কাছে। সেই সঙ্গে আমাদের জীবন ও বাণিজ্যের বাস্তবসম্মত প্রয়োগের দিকেও ফিরতে হবে। মার্ক টোয়েনের বিখ্যাত সেই এক উক্তি, ‘সবাই আবহাওয়া নিয়ে অভিযোগ করে, কিন্তু এটা নিয়ে কেউ কখনো কিছুই করে না।’ আধুনিক সভ্যতা এখনো একটা বজ্রপাতের গতিপথও পরিবর্তন করতে অক্ষম। কিন্তু পদার্থবিদেরা আরও মার্জিত এক প্রশ্ন করেন : আবহাওয়ার পূর্বাভাস কি দেওয়া সম্ভব? এমন কম্পিউটার প্রোগ্রাম কি বানানো সম্ভব, যা দিয়ে পৃথিবীর জটিল আবহাওয়ার প্যাটার্নের পূর্বাভাস দেওয়া যাবে? তা সম্ভব হলে, আবহাওয়া নিয়ে উদ্বিগ্ন সবার জন্য একটা বেশ ব্যবহারিক প্রয়োগ হতো। কারণ, কৃষক জানতে চান, কখন তাদের ফসল লাগাতে হবে। আবহাওয়াবিদ জানতে চান চলতি শতাব্দীতে বৈশ্বিক উষ্ণায়নের গতিবিধি।

তাত্ত্বিকভাবে নিউটনের গতি সূত্র ব্যবহার করে একটা কম্পিউটারের মাধ্যমে আবহাওয়া গঠনকারী এলোমেলো অণুগুলোর গতিপথ প্রায় সঠিকভাবে গণনা করা যাবে। কিন্তু বাস্তবে কম্পিউটার প্রোগ্রাম চরম স্কুল। কয়েক দিন বা তার চেয়ে বেশি সময়ের আবহাওয়ার পূর্বাভাস দেওয়ার জন্য নির্ভরযোগ্যও নয় যন্ত্রটা। কারণ, আবহাওয়ার পূর্বাভাসের জন্য বাতাসের প্রতিটি অণুর গতি নির্ণয় করতে হয়। কাজটা আমাদের সবচেয়ে শক্তিশালী কম্পিউটারেরও ক্ষমতার বাইরে। আবার ক্যাওস থিওরি বা বাটারফ্লাই ইফেক্ট-সংক্রান্ত কিছু সমস্যাও রয়েছে এখানে। বাটারফ্লাই ইফেক্ট অনুসারে, একটা প্রজাপতির ডানার অতি ছোট কম্পনও একটা ঢেউয়ের প্রভাব তৈরি হতে পারে। এ রকম মূল ঘটনাগুলো হয়তো ক্রমে ক্রমে বদলে দিতে পারে শত শত মাইল দূরের আবহাওয়া।

গণিতবিদেরা এ অবস্থাকে সংক্ষিপ্ত করতে বলেন—সবচেয়ে ছোট মডেল যা সঠিকভাবে আবহাওয়াকে ব্যাখ্যা করতে পারে, সেটা হলো ওই আবহাওয়া নিজেই। প্রতিটি অণুর মাইক্রো-অ্যানালাইসিস করা আমাদের পক্ষে কঠিন। আমরা সবচেয়ে ভালো যে কাজটি করতে পারি, তা হলো আগামীকালের আবহাওয়ার অনুমান এবং বৃহত্তর প্রবণতা ও প্যাটার্ন (যেমন গ্রিনহাউস ইফেক্ট) অনুমান করা।

কাজেই দেখা যাচ্ছে, একটা নিউটনের জগৎকে কোনো কম্পিউটারে প্রোগ্রামে নামিয়ে আনা খুব কঠিন। কারণ, এর সঙ্গে অনেকগুলো চলক এবং অনেক বেশি ‘প্রজাপতি’ জড়িত। কিন্তু কোয়ান্টাম জগতে অদ্ভুত সব কাণ্ডকারখানা ঘটতে পারে।

আমরা আগেই দেখেছি, বেকেস্টাইন প্রমাণ করেছেন, একটা কৃষ্ণগহ্বরে র মোট তথ্যের পরিমাণ তার ঘটনাদিগন্তের পৃষ্ঠতলের ক্ষেত্রফলের সমানুপাতিক। এটা দেখার একটা সহজাত উপায় আছে। অনেক পদার্থবিদের বিশ্বাস, সম্ভাব্য সর্বনিম্ন দূরত্ব হলো ১০^-৩৩ সেন্টিমিটারের প্ল্যাঙ্ক দৈর্ঘ্য। এই অবিশ্বাস্য ক্ষুদ্র দূরত্বে স্থান-কাল আর মসৃণ থাকে না, ফেনাময় হয়ে যায়। এর সঙ্গে ফেনায়িত বুদ্বুদের বেশ মিল। ঘটনাদিগন্তের গোলকীয় পৃষ্ঠতলকে ছোট ছোট বর্গে বিভক্ত করা যায়। তাদের প্রতিটির আকার হবে একেকটি প্ল্যাঙ্ক দৈর্ঘ্যের সমান। এই বর্গগুলোর প্রতিটি যদি একটা বিট তথ্য ধারণ করে এবং সবগুলো বর্গ একত্রে যোগ করা হলে মোটামুটিভাবে কৃষ্ণগহ্বরে থাকা মোট তথ্য নির্ণয় করা যাবে। এটা এসব ‘প্ল্যাঙ্ক বর্গের’ প্রতিটি তথ্যের সর্বনিম্ন একক নির্দেশ করে বলে মনে হয়। এটা সত্যি হলে বেকেস্টাইন দাবি করেন, ক্ষেত্র তত্ত্ব নয়, বরং তথ্য হয়তো পদার্থবিজ্ঞানের সত্যিকার ভাষা। তিনি কথাটা এভাবে বলেছেন, ‘ক্ষেত্র তত্ত্ব, তার অসীমসহ চূড়ান্ত কাহিনি হতে পারে।’

উনিশ শতকে মাইকেল ফ্যারাডের গবেষণার পর পদার্থবিদ্যাকে ফিল্ড বা ক্ষেত্রের ভাষায় সূত্রবদ্ধ করা হয়। ক্ষেত্র মসৃণ ও চলমান। চুম্বকীয়, বৈদ্যুতিক ও মহাকর্ষসহ স্থান-কালের যেকোনো বিন্দুতে শক্তিমত্তার পরিমাণ মাপে এটি। কিন্তু ক্ষেত্র তত্ত্বের ভিত্তি হলো অবিচ্ছিন্ন কাঠামো; ডিজিটালাইজড কিছু নয়। একটা ক্ষেত্র যেকোনো মান দখল করতে পারে। সেখানে ডিজিটালাইজড সংখ্যা ০ ও ১ ভিত্তিক শুধু বিচ্ছিন্ন সংখ্যার প্রতীক। এটাই আইনস্টাইনের তত্ত্বে পাওয়া একটা মসৃণ রাবারের পাত আর একটা সূক্ষ্ম তারের জালের মধ্যে পার্থক্য। রাবারের পাতকে অসীমসংখ্যক বিন্দুতে ভাগ করা যায়, কিন্তু তারের জালে থাকে একটা সর্বনিম্ন দূরত্ব, জালের ফাঁকা ঘরের দৈর্ঘ্য।

বেকেস্টাইনে প্রস্তাব হলো, ‘একটা চূড়ান্ত তত্ত্বকে শুধু ক্ষেত্রগুলো নয়, এমনকি স্থান-কালও নয়, বরং ভৌত প্রক্রিয়ার মধ্যে যেসব তথ্যের আদান- প্রদান হয়, তা অবশ্যই আমলে নিতে হবে।’

মহাবিশ্ব যদি ডিজিটালাইজড হতে পারে এবং ০ ও ১-তে নেমে আসে, তাহলে মহাবিশ্বের মোট তথ্যের পরিমাণ কত হবে? বেকেস্টাইন হিসাব করে দেখেছেন, এক সেন্টিমিটার জায়গাজুড়ে থাকা একটা কৃষ্ণগহ্বরে ১০^৬৬ বিট তথ্য থাকতে পারে। কিন্তু এক সেন্টিমিটার আকারের বস্তু এর চেয়েও বেশি বিট তথ্য ধারণ করা গেলে, হিসাব করে দেখেছেন দৃশ্যমান মহাবিশ্ব সম্ভবত অনেক বেশি তথ্য ধারণ করতে পারবে। তার পরিমাণ কোনোভাবেই ১০^১০০ বিট তথ্যের কম নয়। (একে তাত্ত্বিকভাবে এক আলোকবর্ষের দশ ভাগের এক ভাগ সমান এক গোলকে সংকুচিত করে রাখা সম্ভব। ১-এর পর ১০০টি শূন্য সম্পন্ন বিশাল এ সংখ্যাকে বলা হয় এক গুগল।)

এই মডেলটি সঠিক হলে আমাদের অদ্ভুত একটা অবস্থায় থাকার কথা। এর মানে এমনও হতে পারে, নিউটোনিয়ান জগৎ যেখানে কম্পিউটারের সিমুলেট করা যায় না (কিংবা একে শুধু তার মতো সমান কোনো সিস্টেমের মাধ্যমেই সিমুলেট করা সম্ভব), কোয়ান্টাম জগতে হয়তো খোদ মহাবিশ্বকে একটা সিডিতে রাখা হয়েছে! তাত্ত্বিকভাবে, একটা সিডিতে যদি ১০^১০০ বিট তথ্য রাখা হয়, তাহলে আমাদের মহাবিশ্বে যেকোনো ঘটনা উন্মোচিত হতে দেখা যাবে বসার ঘরে বসে থেকেই। নীতিগতভাবে, যে কেউ ওই সিডির বিট নতুন করে সাজাতে বা নতুনভাবে প্রোগ্রাম করতে পারবে। তাই ভৌত বাস্তবতা বিভিন্নভাবে এগিয়ে যাবে। কিছু অর্থে বলা যায়, স্ক্রিপ্টটা নতুন করে লেখার জন্য দরকার হবে দেবতাদের মতো ক্ষমতা।

(বেকেস্টাইন এটাও স্বীকার করেছেন, মহাবিশ্বের মোট তথ্যের পরিমাণ এর চেয়েও বেশি হতে পারে। আসলে ক্ষুদ্রতম যে আয়তনে মহাবিশ্বের সবগুলো তথ্য ধারণ করতে পারবে, সেটা হলো মহাবিশ্বের নিজের আকার। এটা সত্যি হলে, আমরা যেখান থেকে শুরু করেছিলাম আবারও সেখানেই ফিরে যাব। মোদ্দা কথায়, ক্ষুদ্রতম যে ব্যবস্থা এই মহাবিশ্বের মডেল হতে পারে, সেটা হলো মহাবিশ্ব নিজেই।

তবে ক্ষুদ্রতম দূরত্ব এবং আমরা এই মহাবিশ্বকে একটা সিডিতে ডিজিটালাইজড করতে পারব কি না, তা নিয়ে কিছুটা ভিন্ন ধরনের ব্যাখ্যা দেয় স্ট্রিং থিওরি। এম-তত্ত্বে একে বলা হয় টি-ডুয়ালিটি। মনে আছে নিশ্চয়ই, গ্রিক দার্শনিক জেনো একটা রেখাকে অসীমসংখ্যক বিন্দুতে বিভক্ত করেছিলেন। সেগুলোর কোনো সীমা ছিল না। বর্তমানে বেকেস্টাইনের মতো কোয়ান্টাম পদার্থবিদেরা বিশ্বাস করেন, সর্বনিম্ন দূরত্ব হলো ১০^-৩৩ সেন্টিমিটারের প্ল্যাঙ্ক দূরত্ব। এই দূরত্বে স্থান-কালের নকশা হয়ে যায় ফেনাময় ও বুদ্‌দময়। কিন্তু এম-তত্ত্ব নুতন চমক দেয়। ধরা যাক, একটা স্ট্রিং থিওরি নিয়ে একটা মাত্রাকে R ব্যাসার্ধের একটা বৃত্তের মধ্যে গুটিয়ে ফেলা হলো। এরপর আরেকটা স্ট্রিং নিয়ে তা আটকে ফেললাম এক মাত্রার 1/R ব্যাসার্ধের একটা বৃত্তের ভেতর। এই দুটি ভিন্ন তত্ত্বকে তুলনা করে একসময় দেখা যাবে, তারা আসলে হুবহু একই জিনিস।

এখন ধরা যাক, R অতি ক্ষুদ্র হয়ে গেল, অর্থাৎ প্ল্যাঙ্ক দৈর্ঘ্যের চেয়েও অনেক ছোট। এর মানে, প্ল্যাঙ্ক দৈর্ঘ্যের ভেতরের পদার্থবিজ্ঞান প্ল্যাঙ্ক দৈর্ঘ্যের বাইরের পদার্থবিজ্ঞানের মতো হুবহু এক। প্ল্যাঙ্ক দৈর্ঘ্যে স্থান-কাল হয়তো পিণ্ডাকৃতির ও ফেনাময় হয়ে উঠতে পারে। কিন্তু প্ল্যাঙ্ক দৈর্ঘ্যের ভেতরের পদার্থবিজ্ঞান এবং অনেক বড় দূরত্বের পদার্থবিজ্ঞান মসৃণ হতে পারে এবং আসলে একই রকম হতে পারে।

এই দ্বৈততা প্রথম পাওয়া গিয়েছিল ১৯৮৪ সালে। এটা খুঁজে পান ওসামা বিশ্ববিদ্যালয়ে আমার সহকর্মী কেইজি কিক্কাওয়া এবং তাঁর ছাত্র মাসামি ইয়ামাসামি। স্ট্রিং থিওরি আপাতদৃষ্টে সিদ্ধান্ত নেয় যে সর্বনিম্ন একটা দূরত্ব আছে, অর্থাৎ প্ল্যাঙ্ক দৈর্ঘ্য। কিন্তু পদার্থবিজ্ঞান হঠাৎ করে প্ল্যাঙ্ক দৈর্ঘ্যে এসে শেষ হয়ে যায় না। এই নতুন চমকটি হলো, প্ল্যাঙ্ক দৈর্ঘ্যের চেয়ে ছোট পদার্থবিজ্ঞান আর প্ল্যাঙ্ক দৈর্ঘ্যের চেয়ে বড় পদার্থবিজ্ঞানের সমতুল্য।

এই বিভ্রান্তিকর বা উল্টো ব্যাখ্যাটি সঠিক হলে তার মানে দাঁড়ায়, স্ট্রিং থিওরির সর্বনিম্ন দূরত্বের ভেতর অস্তিত্ব থাকতে পারে গোটা একটা মহাবিশ্ব। অন্য কথায়, মহাবিশ্বকে ব্যাখ্যা করতে আমরা এখনো অবিচ্ছিন্ন (ডিজিটালাইজড নয়) কাঠামোসহ ক্ষেত্র তত্ত্ব ব্যবহার করতে পারি। এমনকি প্ল্যাঙ্ক শক্তির ভেতরের দূরত্বের জন্যও কথাটি সত্যি। কাজেই মহাবিশ্ব হয়তো মোটেও কোনো কম্পিউটার প্রোগ্রাম নয়। যেকোনো ঘটনা, যতক্ষণ তাতে সুসংজ্ঞায়িত করার সমস্যা থাকবে, সময়ই তার উত্তরও বলে দেবে।

(এই টি-ডুয়ালিটি হলো ভেনেজিয়ানোর প্রি-বিগ ব্যাং বা মহাবিস্ফোরণের আগের মডেলের বৈধ্যতা। এর কথা আগেই বলেছি। এ মডেলে একটা কৃষ্ণগহ্বর চুপসে প্ল্যাঙ্ক দৈর্ঘ্যে চলে যায়। তারপর ছিটকে মহাবিস্ফোরণে ফিরে আসে। এই ছিটকে ওঠাটা হঠাৎ ঘটা ঘটনা নয়, বরং প্ল্যাঙ্ক দৈর্ঘ্যের চেয়ে ছোট একটা কৃষ্ণগহ্বর এবং প্ল্যাঙ্ক দৈর্ঘ্যের চেয়ে বড় একটা প্রসারণশীল মহাবিশ্বের মধ্যকার মসৃণ টি-ডুয়ালিটি।)

সমাপ্তি

এম-তত্ত্ব যদি সফল হয়, মোদ্দা কথায়, এটা যদি সত্যিই কোনো থিওরি অব এভরিথিং হয়, তাহলে আমরা এখন যে পদার্থবিজ্ঞানকে জানি বা বুঝি, তার কি সমাপ্তি ঘটবে?

এর উত্তর হলো : না। একটা উদাহরণ দেওয়া যাক। দাবার খেলার নিয়মকানুন আমাদের জানা থাকলেও, শুধু এসব নিয়মকানুন জেনেই কেউ গ্র্যান্ডমাস্টার হয়ে যেতে পারে না। একইভাবে, মহাবিশ্বের নিয়মকানুন জানা মানেও এই নয় যে আমরা উন্নত ধরনের সমাধান বোঝার মতো কোনো গ্র্যান্ডমাস্টার হয়ে গেছি।

ব্যক্তিগতভাবে, আমি মনে করি, মহাবিশ্বের ক্ষেত্রে এম-তত্ত্ব এখনো প্ৰয়োগ করাটা সঠিক সময়ের আগে হয়ে যাবে। অবশ্য মহাবিশ্ব কীভাবে শুরু হতে পারে, সে সম্পর্কে তত্ত্বটা আমাদের হাতে অভিনব একটা চিত্রের জোগান দিয়েছে সত্যি, কিন্তু তারপরও। আমার ধারণা, এখানে প্রধান সমস্যাটি হলো এই মডেলটির চূড়ান্ত রূপ এখনো আমাদের হাতে আসেনি। এম-তত্ত্ব হয়তো বেশ ভালোভাবেই থিওরি অব এভরিথিং বা সার্বিক তত্ত্ব হতে পারে। কিন্তু আমার বিশ্বাস, এর শেষ পর্যায় থেকে এখনো অনেক দূরে রয়ে গেছি। তত্ত্বটি সেই ১৯৬৮ সাল থেকে পেছনের দিকে বিকশিত হচ্ছে। তার চূড়ান্ত সমীকরণগুলো এখনো খুঁজে পাওয়া যায়নি। (যেমন স্ট্রিং থিওরিকে স্ট্রিং ফিল্ড থিওরির মাধ্যমে সূত্রবদ্ধ করা হয়। সেটা আমি এবং কিক্বাওয়া দেখিয়েছি অনেক বছর আগে। এম-তত্ত্বের জন্য এসব সমীকরণের পরিপূরক অংশ এখনো অজানা।

এম-তত্ত্ব বেশ কিছু সমস্যার মুখোমুখি। এর মধ্যে একটা হলো, এখন পি-ব্রেনের মধ্যে হাবুডুবু খাচ্ছেন পদার্থবিজ্ঞানীরা। বিভিন্ন মাত্রায় থাকতে পারা বিচিত্র ধরনের মেমব্রেনদের তালিকা তৈরির চেষ্টা করে ইতিমধ্যে একগুচ্ছ গবেষণা প্রবন্ধ লেখা হয়ে গেছে। এসব মেমব্রেনের আকার অনেকটা মাঝখানে গর্তসহ ডোনাটের মতো, অনেকগুলো গর্তসহ একটা ডোনাটের মধ্যে, ছেদকৃত মেমব্রেন এবং আরও হরেক রকম।

এসব দেখে কয়েকজন অন্ধ জ্ঞানী মানুষের হাতি দর্শনের নীতিকথার গল্পটা এবার মনে করিয়ে দেওয়া যায়। হাতিটির গায়ের বিভিন্ন জায়গা স্পর্শ করে প্রত্যেকে তার নিজের মতো তত্ত্বে পৌঁছেন। এক জ্ঞানী ব্যক্তি হাতির লেজ স্পর্শ করে বললেন, হাতিটি হলো এক-ব্রেন (একটা স্ট্রিং)। আরেক জ্ঞানী ব্যক্তি হাতির কান স্পর্শ করে বললেন, হাতিটি একটা দুই-ব্রেন (একটা মেমব্রেন)। পরে সর্বশেষ জন বলেন, অন্য দুই জ্ঞানী ব্যক্তি ভুল বলেছেন। হাতির পা স্পর্শ করে তার কাছে গাছের গুঁড়ির মতো লাগল। তাই তৃতীয় জ্ঞানী ব্যক্তি বলে উঠলেন, হাতিটি আসলে তিন-ব্রেন। এই তিন জ্ঞানী অন্ধ হওয়ার কারণে বড় পরিসরের ছবিটি দেখতে পান না। সোজা কথায়, এক-ব্রেন, দুই-ব্রেন এবং তিন-ব্রেনের সমষ্টি দেখতে পান না। আর সমষ্টি আসলে একক একটা প্রাণী, একটা বিশালাকৃতির হাতি।

একইভাবে বিশ্বাস করাও শক্ত যে এম-তত্ত্বে যেসব শত শত মেমব্রেন পাওয়া যায়, তা কোনো না কোনোভাবে মৌলিক। বর্তমানে আমরা এম- তত্ত্ববিষয়ক সমন্বিত কোনো উপলব্ধিতে পৌছাতে পারিনি। আমার দৃষ্টিভঙ্গিটি বর্তমানে নিজের চলমান গবেষণাকে পরিচালিত করছে। সেটা হলো, এসব স্ট্রিং ও মেমব্রেন স্থানের সংক্ষিপ্তকরণ প্রকাশ করে। এককালে বস্তুকে বিশুদ্ধ জ্যামিতিক পরিভাষায় ব্যাখ্যা করার চেষ্টা করেছিলেন আইনস্টাইন। সেটা স্থান-কালের নকশায় কোনো এক ধরনের ফিতা বা গিঁটের মতো। যেমন আমাদের কাছে যদি একটা বিছানার চাদর থাকে, তাহলে একটা গিঁট বানানো সম্ভব। সেই গিঁটটা এমন আচরণ করবে যেন তার নিজেরও একটা জীবন আছে। ইলেকট্রন ও অন্যান্য মৌলিক কণাকে স্থান-কালের জ্যামিতিতে কোনো এক ধরনের গোলমালের মডেল হিসেবে উপস্থাপনের চেষ্টা করেছেন আইনস্টাইন। শেষ পর্যন্ত তিনি ব্যর্থ হলেও এই ধারণা হয়তো এম-তত্ত্বের উচ্চতর পর্যায়ে ফিরেও আসতে পারে।

আমার বিশ্বাস, আইনস্টাইন সঠিক পথেই ছিলেন। তাঁর ধারণাটা ছিল জ্যামিতির মাধ্যমে অতিপারমাণবিক পদার্থবিজ্ঞানের জন্ম দেওয়া। আইনস্টাইনের কৌশলটা ছিল, বিন্দু কণাদের একটা জ্যামিতিক তুল্যতা তৈরির চেষ্টা করা। তা না করে, একে সংশোধন করে স্ট্রিং আর মেমব্রেনের জ্যামিতিক তুল্যতা তৈরির চেষ্টা করে বিশুদ্ধ স্থান-কাল বানানো যেতে পারে।

এই পদ্ধতির যুক্তিটি দেখার একটা উপায় হলো, পদার্থবিজ্ঞানের ইতিহাসের দিকে নজর দেওয়া। অতীতে পদার্থবিদেরা যখনই কোনো বস্তুর বর্ণালির মুখোমুখি হতেন, তখন বোঝা যেত, এর মূলে আরও মৌলিক কিছু আছে। যেমন হাইড্রোজেন গ্যাস থেকে নিঃসৃত বর্ণালি রেখা আবিষ্কারের পর বোঝা গেল যে তাদের উৎপত্তি আসলে পরমাণু থেকে। অর্থাৎ পরমাণুর নিউক্লিয়াসের ঘূর্ণমান ইলেকট্রনের কোয়ান্টাম লাফের কারণে তার জন্ম। একইভাবে ১৯৫০-এর দশকে শক্তিশালী কণার দ্রুত বিস্তারের মুখোমুখি হওয়ার পর পদার্থবিদেরা ধীরে ধীরে বুঝতে পারলেন, সেগুলো আসলে কোয়ার্কের বন্ধন দশা ছাড়া আর কিছুই নয়। আবার কোয়ার্ক ও স্ট্যান্ডার্ড মডেলের অন্যান্য মৌলিক কণার বিস্তারের সম্মুখীন হয়ে অধিকাংশ পদার্থবিদ বিশ্বাস করলেন, স্ট্রিংয়ের কম্পনের কারণে তাদের উৎপত্তি হচ্ছে।

এম-তত্ত্বসহ আমরা বিভিন্ন ধরনের ও জাতের পি-ব্রেনের বিস্তারের মুখোমুখি হয়েছি। বিশ্বাস করাও কঠিন যে এসব মৌলিক হতে পারে। এতে খুবই সরল পি-ব্রেনের কারণে এবং তারা সহজাতভাবে অস্থিতিশীল ও বিচ্ছিন্ন হওয়ার কারণে এমন মনে হয়েছিল। তুলনামূলক সহজ সমাধানে (যা ঐতিহাসিক পদ্ধতির সঙ্গে মিলে যায়) অনুমান করা হলো, এম-তত্ত্ব আরও সরলতম কিছু থেকে উদ্ভব হয়েছে, হয়তো খোদ জ্যামিতি থেকেই।

মৌলিক প্রশ্নগুলোর সমাধানের জন্য, শুধু তার রহস্যময় গণিতই নয়, ওই তত্ত্বের অন্তর্নিহিত ভৌত নীতিও জানা দরকার। পদার্থবিদ ব্রায়ান গ্রিন বলেন, ‘বর্তমানে, স্ট্রিং তাত্ত্বিকেরা এমন এক অবস্থানে আছেন, যার সঙ্গে আইনস্টাইনের সমতুল্যতা নীতির সাধনার তুলনা চলে। ১৯৬৮ সালে ভেনেজিয়ানোর অন্তর্দৃষ্টির পর থেকে তত্ত্বটির বিভিন্ন টুকরো টুকরো অংশ একত্র করা হয়েছে। একের পর এক আবিষ্কারের পর আবিষ্কার হয়েছে। বিপ্লবও হয়েছে একের পর। কিন্তু কেন্দ্রীয় সাংগঠনিক নীতিটি যা তত্ত্বটির এসব আবিষ্কার ও সবগুলো বৈশিষ্ট্যকে একটা খিলান ও পদ্ধতিগত কাঠামোকে অবলম্বন করে, তেমন কিছু এখনো পাওয়া যায়নি। এটা এমন এক কাঠামো, যা প্রতিটি উপাদানকে অনিবার্য করে তুলবে পরমভাবে। এই নীতির আবিষ্কারকে স্ট্রিং থিওরির বিকাশের একটা গুরুত্বপূর্ণ মুহূর্ত হিসেবে চিহ্নিত করবে। কারণ, সম্ভবত এটা তত্ত্বটির অভ্যন্তরীণ কর্মকাণ্ডকে প্রকাশ করবে অপ্রত্যাশিত স্পষ্টতার সঙ্গে।

স্ট্রিং তত্ত্বের জন্য খুঁজে পাওয়া কোটি কোটি সমাধানকেও বোধগম্য করে তুলবে এটা। এসব সমাধানের প্রতিটি পরিপূর্ণভাবে একেকটা স্বনির্ভর মহাবিশ্বের প্রতিনিধিত্ব করবে। অতীতে ধারণা ছিল, এসব অগণিত সমাধানের জঙ্গলে মাত্র একটাই স্ট্রিং থিওরির সত্যিকার সমাধান তুলে ধরে। বর্তমানে আমাদের চিন্তাধারা বদলে গেছে। এখন পর্যন্ত কোটি কোটি মহাবিশ্ব থেকে মাত্র একটাকে নির্বাচন করার উপায় নেই। মতামতের ক্রমবর্ধমান কলেবর জানাচ্ছে যে স্ট্রিং থিওরির কোনো অনন্য সমাধানটি খুঁজে পাওয়া গেলে, তার কারণ সম্ভবত আসলে তেমন কিছু একটাও নেই। সব সমাধানই সমান। মহাবিশ্বগুলোর একটা মাল্টিভার্স আছে। এদের প্রতিটি পদার্থবিজ্ঞানের সব সূত্র ধারণ করে। তাহলে এটি অ্যানথ্রোপিক প্রিন্সিপল ও একটা ডিজাইনার ইউনিভার্সের সম্ভাবনার আভাস দেয়।

তথ্যনির্দেশ

টেসারেক্ট : জ্যামিতিতে ঘনকসদৃশ চতুর্থমাত্রিক বস্তু।

ইকপাইরোটিক মহাবিশ্ব : আদিম মহাবিশ্বের জন্য একটা সৃষ্টিতাত্ত্বিক মডেল। এটি বিশ্বজগতের বৃহৎ পরিসরের কাঠামোর উৎপত্তি ব্যাখ্যা করে। ২০০১ সালে জাস্টিন কোরি, ব্রাট ওভরুট, পল স্টেইনহার্ট এবং নীল টুরোক এই মডেলের প্রস্তাব করেন।

সুপারসিমেট্রি বা অতিপ্রতিসাম্যতা : এ তত্ত্বটি ১৯৭১ সালে প্রস্তাব করেছিলেন রুশ বিজ্ঞানী ইউজেনি লিখটম্যান এবং উইরি গলফ্যান্ড। এ ধারণায় তাঁরা কণাগুলো আর মিথস্ক্রিয়ার মধ্যে নতুন প্রতিসাম্যতার কথা বলেছিলেন। এই তত্ত্বমতে, প্রকৃতিতে প্রতিটি মৌলিক কণার অতিপ্রতিসাম্য সঙ্গী বা সুপার পার্টনার আছে। তবে এদের দেখতে পাওয়া যাবে না। এ ক্ষেত্রে ফোটনের সুপার পার্টনারের নাম দেওয়া হয়েছে ফোটিনো।

এনথ্রোপিক প্রিন্সিপাল : আমরা এই মহাবিশ্ব এভাবে দেখি; কারণ, এটি যদি অন্য রকম হতো, তাহলে একে পর্যবেক্ষণ করার জন্য হয়তো আমাদের অস্তিত্বই থাকত না, এই ধারণা।

কণা ত্বরণযন্ত্র : যে যন্ত্রের সাহায্যে বিদ্যুৎ-চুম্বক ব্যবহার করে চার্জিত কণাগুলোকে অনেক বেশি শক্তি দান করে গতিশীল করতে পারা যায়।

দ্বৈততা (Duality) : আপাতদৃষ্টে দুটি আলাদা তত্ত্বের মধ্যে সাদৃশ্যতা, যা দিয়ে এই ভৌত ফলাফল পাওয়া যায়।