১২. ভালোরা সফল হয়

অধ্যায় ১২ : ভালোরা সফল হয়

নাইস গাইস ফিনিশ লাস্ট (ভালো মানুষদের অসফল হবার প্রবণতা আছে) প্রবাদ বাক্যটি মনে হয় উদ্ভব হয়েছে বেসবল খেলার জগতে, যদিও কিছু কতৃপক্ষ এর একটি বিকল্প অর্থের অগ্রাধিকার দাবী করে আসছেন। আমেরিকার জীববিজ্ঞানী গ্যারেট হারডিন এটি ব্যবহার করেছিলেন সেই বিষয়টির সারাংশ হিসাবে প্রকাশ করতে, যে বিষয়টির শিরোনাম দেয়া যেতে পারে ‘সোসিওবায়োলজী অথবা ‘সেলফিশ জিনেরী। এই যথার্থতা খুব সহজেই দেখা যেতে পারে। যদি ‘নাইস গাই’ শব্দটির চলিত কথ্য ভাষার অর্থটি ডারউইনীয় সমার্থক শব্দার্থে অনুবাদ করি, একজন ‘নাইস’ গাই হচ্ছে সেই সদস্য, যে নিজে মূল্য পরিশোধ করার বিনিময়ে প্রজাতির অন্যান্য সদস্যদেরকে তাদের জিন পরবর্তী প্রজন্মে হস্তান্তরিত করতে সহায়তা করে। তাহলে নাইস গাইস বা এই সব ভালো সদস্যদের সংখ্যা প্রজাতির সদস্যদের মধ্যে কমে যেতে বাধ্য: এই পরোপকারীতা একটি ডারউইনীয় মৃত্যুর শিকার হয়। কিন্তু কথ্য ‘নাইস’ শব্দটির আরো একটি কারিগরী ব্যাখ্যা আছে। আমরা যদি সেই সংজ্ঞাটিকে গ্রহন করে নেই, যা শব্দটির কথ্য রুপের অর্থ থেকে খুব বেশী দূরে নয়, ‘নাইস গাইস ক্যান ফিনিস ফার্স্ট’ বা ভালো সদস্যরা সফল হতে পারে। এই আরো বেশী আশাবাদী উপসংহারটি হচ্ছে এই অধ্যায়ের মূল বিষয়।

অধ্যায় ১০ এ উল্লেখিত ‘গ্রাজারদের কথা মনে করুন। এরা ছিল পাখি, যারা সাধারণত একে অপরকে সাহায্য করে আপাতদৃষ্টিতে একটি পরার্থবাদী উপায়ে, কিন্তু তারা সাহায্য করতে অস্বীকার করে– গ্রাজ কিংবা ক্ষোভ ধারণ করে তাদের বিরুদ্ধে– সেই সব সদস্যদের যারা এর আগে তাদেরকে সাহায্য করতে অস্বীকার করেছে। গ্রাজাররা জনগোষ্ঠীতে প্রাধান্য বিস্তার করে কারণ তারা যেকোনো ‘সাকার’ (যারা নির্বিচারে সবাইকে সাহায্য করে, এবং সেকারণে সবাই নিজস্ব স্বার্থসিদ্ধির উদ্দেশ্যে তাদের ব্যবহার করতে পারে) অথবা “চিটদের’ (যারা সবাইকে তাদের নিজেদের স্বার্থে ব্যবহার করতে নিষ্ঠুরভাবে চেষ্টা করে, পরিণতিতে পরস্পরের ক্ষতি করে) তুলনায় অনেক বেশী জিন তাদের পরবর্তী প্রজন্মে হস্তান্তর করতে সফল হয়। গ্রাজারদের কাহিনী একটি গুরুত্বপূর্ণ সাধারণ মূলনীতিকে ব্যাখ্যা করে, রবার্ট ট্রিভার্স যার নাম দিয়েছিলেন ‘রেসিপ্রকোল আলট্রইজম’ বা পারস্পরিক পরার্থবাদিতা। আমরা যেমন ক্লিনার ফিশদের উদাহরণে দেখেছিলাম ( মূল বইয়ের পৃষ্ঠা ২৪৩-৪), পারস্পরিক পরার্থবাদীতা শুধুমাত্র একটি প্রজাতির সদস্যদের মধ্যেই সীমাবদ্ধ নয়। এটি সব ধরনের সম্পর্কেই কাজ করে, যাদের বলা হয় সিমবায়োটিক (মিথোজীবি)– যেমন, পিপড়াদের তাদের এফিড ‘গবাদী’ থেকে দুধ সংগ্রহ করার আচরণ (মূল বইয়ের পৃষ্ঠা ২৩৫-৬)। অধ্যায় ১০ লেখা শেষ করার পরে, আমেরিকার রাষ্ট্রবিজ্ঞানী রবার্ট অ্যাক্সেলরড (যিনি ডাবলিউ, ডি, হ্যামিলটনের সাথে কাজ করেছিলেন, যার নাম এই বইয়ের বহু পাতায় আমরা দেখতে পাবো) এই রেসিপ্রোকাল অ্যালট্রইজিমের ধারণাটিকে একটি উত্তেজনাময় নতুন দৃষ্টিভঙ্গিতে ব্যাখ্যা করেছিলেন। এবং অ্যাক্সেলরডই প্রথম ব্যাক্তি যিনি ‘নাইস’ শব্দটির একটি কারিগরী অর্থ প্রস্তাব করেছিলেন, আমি শুরুর অনুচ্ছেদে যে অর্থটির প্রতি তথ্য-নির্দেশ করেছি।

অ্যাক্সেলরড, আরো অনেক রাষ্ট্রবিজ্ঞানী, অর্থনীতিবিদ এবং গণিতজ্ঞ ও মনোবিজ্ঞানীর মত একটি সরল জুয়া খেলার প্রতি আকৃষ্ট হয়েছিলেন, যা পরিচিত ‘প্রিজনার’স ডাইলেমা’ নামে। এটি এত সরল যে, আমি দেখেছি বুদ্ধিমান মানুষরা এটি পুরোপুরিভাবে ভুল বোঝেন, তারা ভাবেন নিশ্চয়ই এর মধ্যে আরো কিছু আছে। কিন্তু এর সরলতাই চোখকে আসলে ফাঁকি দেয়। এই ধাঁধা লাগানো খেলার নানা ধরনের বিশ্লেষণে নিবেদিত বই লাইব্রেরীর পুরো তাক জুড়ে দেখা যায়। অনেক প্রভাবশালী ব্যক্তি মনে করেন এর মধ্যেই আছে কৌশলগত প্রতিরক্ষা পরিকল্পনা এবং তৃতীয় বিশ্বযুদ্ধ প্রতিরোধ করার জন্য আমাদের এটি ভালো করে পড়া উচিৎ। জীববিজ্ঞানী হিসাবে, আমি অ্যাক্সেলরড এবং হ্যামিলটনের সাথে একমত যে, বহু বন্য প্রাণী এবং উদ্ভিদ ‘প্রিজনার’স ডাইলেমা’র অন্তহীন খেলাগুলো নিয়েই নিরন্তরভাবেই ব্যস্ত, বিবর্তনীয় সময়ের প্রেক্ষাপটে যা তারা খেলে যাচ্ছে।

মানব সংশ্লিষ্ট এর মূল সংস্করণে, এই খেলাটি যেভাবে খেলা হয়ে থাকে সেটি হচ্ছে একরম: একজন ‘ব্যাঙ্কার’ আছেন, যিনি বিচার করে সিদ্ধান্ত প্রদান করেন ও দুই খেলোয়াড়ের মধ্যে খেলার অর্জিত লভ্যাংশ ভাগ করে দেন। মনে করুন, আমি আপনার বিরুদ্ধে খেলছি। (যদিও, আমরা পরে দেখবো, ‘বিরুদ্ধে’ হচ্ছে ঠিক সেই অবস্থান যে অবস্থানে আমাদের থাকার কোনো প্রয়োজন নেই)। আমাদের প্রত্যেকের হাতে কেবল দুটি কার্ড আছে, যেগুলো হচ্ছে– ‘কোঅপারেট’ বা সহযোগিতা এবং ‘ডিফেক্ট’ বা অসহযোগিতা বা বিশ্বাসঘাতকতা। খেলার জন্য, প্রত্যেককেই আমাদের হাতের এই দুটি কার্ডের থেকে যেকোনো একটি কার্ডকে বেছে নিতে হবে এবং সেটিকে উপুড় করে রাখতে হবে টেবিলের উপর। উপুড় করে কারণ, আমরা কেউ দেখবো না কার্ডটি কি, আমাদের দুজনের কেউই অন্যদের খেলা দ্বারা প্রভাবিত হবে না। কার্যত যা হচ্ছে আমরা যুগপৎভাবে এই দানটি খেলবো। এরপর আমরা আগ্রহ নিয়ে অপেক্ষা করবো ব্যাঙ্কার যখন কার্ডটি সোজা করে দেখবেন। এই টানটান উত্তেজনার কারণ আমাদের লভ্যাংশ নির্ভর করবে শুধুমাত্র কোন কার্ড আমরা খেলেছি (যা আমরা দুজনেই পৃথকভাবেই জানি) তার উপরেই, বরং অন্য খেলোয়াড় কোন কার্ডটি খেললেন তার উপরেও ( সেটা আমরা জানিনা যতক্ষণ না ব্যাঙ্কার সেটি আমাদের সামনে তুলে ধরছেন)।

 যেহেতু ২ x ২ সংখ্যক কার্ড আছে, এখানে মোট চারটি সম্ভাব্য ফলাফল হতে পারে। প্রতিটি ফলাফলের জন্য, আমাদের লাভ হচ্ছে এরকম: (উত্তর আমেরিকায় খেলাটি আবিষ্কার হয়েছে, সেই কথা বিবেচনা করে ডলার হিসাবে উল্লেখ করা হয়েছে):

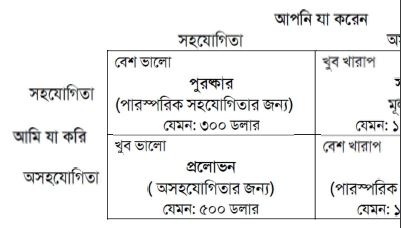
আউটকাম ১: আমরা দুজনেই ‘কো-অপারেট’ কার্ড টি খেলেছি। ব্যাঙ্কার আমাদের দুজনকেই ৩০০ ডলার করে দেবে। এই সম্মানজনক পরিমান টাকাকে বলা হচ্ছে পারস্পরিক সহযোগিতার জন্য পুরষ্কার।

আউটকাম ২: আমরা দুজনেই ‘ডিফেক্ট’ কার্ডটি খেলেছি। ব্যাঙ্কার আমাদের দুজনকে ১০ ডলার করে জরিমানা করে। এই পরিমান টাকাকে বলা হচ্ছে পারস্পরিক বিশ্বাসঘাতকতা বা অসহযোগিতার বা ডিফেক্টশনের জন্য শাস্তি।

আউটকাম ৩: যদি আপনি কো-অপারেট’ কার্ডটি খেলেন এবং আমি ‘ডিফেক্ট’ কার্ডটি খেলে থাকি। ব্যাঙ্কার আমাকে ৫০০ ডলার দেবে (অসহযোগিতার করার প্রলোভন সাড়া দেবার জন্যে) এবং আপনাকে জরিমানা করে (সাকার’) ১০০ ডলার।

আউটকাম ৪: যদি আপনি ‘ডিফেক্ট’ কার্ডটি খেলেন এবং আমি ‘কো-অপারেটিভ কার্ডটি খেলে থাকি। ব্যাঙ্কার আপনাকে ৫০০ ডলার দেবে (অসহযোগিতার করার প্রলোভনে সাড়া দেবার জন্যে। এবং আমাকে জরিমানা করা হবে (“সাকার’) ১০০ ডলার।

আউটকাম ৩ ও ৪ অবশ্যই এক দৃশ্যের আয়না-প্রতিবিম্ব: একজন খেলোয়াড় খুবই ভালো করে, অন্যজন খুব খারাপ।

আউটকাম ১ ও ২ এ আমরা দুজনেরই অর্জন সমপরিমান {১ এ মাথাপিছু ৩০০ ডলার, আর ২ এ মাথাপিছু ক্ষতি ১০ ডলার), কিন্তু আউটকাম ২ অপেক্ষা আউটকাম ১ আমাদের দুজনের জন্যই অপেক্ষাকৃত অনেক ভালো। সত্যিকার টাকার পরিমান এখানে আলোচ্য কিছু নয়, এমনকি গুরুত্বপূর্ণ নয় তাদের মধ্যে কয়টি পজিটিভ (টাকা পরিশোধ) এবং তাদের মধ্যে কয়টি নেগেটিভ (জরিমানা)। এই খেলাটিকে একটি সত্যিকারের প্রিজনার’স ডাইলেমা হিসাবে যোগ্য হবার জন্য যা গুরুত্বপূর্ণ, সেটি হচ্ছে তাদের র‍্যাঙ্ক অর্ডার বা আউটকামগুলোর ক্রমানুসরতা। পারস্পরিক সহযোগিতার করার মাধ্যমে অর্জিত পুরস্কারের তুলনায় অসহযোগিতা বা বিশ্বাসঘাতকতা করার প্রলোভন অবশ্যই উত্তম, যা অবশ্যই উত্তম পারস্পরিক অসহযোগিতা থেকে, যা অবশ্যই উত্তম সাকাররা যে পরিমান টাকা পায় তার চেয়েও (কঠোরভাবে বললে, এই খেলার আরো একটি শর্ত আছে, যা এটিকে সত্যিকার প্রিজনার’স ডাইলেমা হিসাবে যোগ্য করে তোলে: প্রলোভন এবং সাকারদের পরিশোধিত মূল্যের গড় অবশ্যই পুরস্কারের চেয়ে বেশী যেন না হয়। এই বাড়তি শর্তের কারণ পরবর্তীতে স্পষ্ট হবে।) চারটি ফলাফল বা আউটকামের সংক্ষিপ্ত ব্যাখ্যা আমরা নিচের ছবি ১ এ কে কত টাকা পেল সেই পে-অফ ম্যাট্রিক্সে দেখতে পাবো:

 কিন্তু, ডাইলেমা বা উভয়সংকট’ কেন? এটি দেখতে হলে, উপরের পে-অফ ম্যাট্রিক্স বা লাভ-ক্ষতির ছকটি লক্ষ করুন এবং কল্পনা করুন সেই সব চিন্তাগুলো যা আমার মাথায় এসেছিল, যখন আমি আপনার বিরুদ্ধে খেলছিলাম। আমি জানি খেলার জন্য মাত্র দুটি কার্ড আছে, ‘কোঅপারেট’ এবং ‘ডিফেক্ট’। এবার তাদের পর্যায়ক্রমে বিবেচনা করা যাক। আপনি যদি ডিফেক্ট অসহযোগিতা কার্ড খেলে থাকেন (এর অর্থ হচ্ছে আমাদের উপরের ডানদিকের কলামটা লক্ষ করতে হবে)।

সবচেয়ে ভালো যে কার্ডটা আমি খেলতে পারি সেটিও ডিফেক্ট অসহযোগিতা। স্বীকার করছি যে, আমি পারস্পরিক অসহযোগিতার কারণে প্রাপ্ত শাস্তির ভুক্তভোগী, কিন্তু যদি আমি সহযোগিতা করি আমি তাহলে ‘সাকার’ এর বিনিময় মূল্য পাবো যা কিনা আরো খারাপ (১০০ ডলার জরিমানা)। এবার তাহলে দেখুন আর কি আপনি করতে পারেন (বাম-দিকে কলামের দিকে তাকান), সহযোগিতার কার্ডটি খেলতে পারেন। আবারও ‘ডিফেক্ট’ বা অসহযোগিতা আমার জন্য সবচেয়ে ভালো পদক্ষেপ। যদি আমি সহযোগিতা করি, তাহলে আমরা দুজনেই বেশ বড় মাপের টাকা, মাথাপিছু ৩০০ ডলার করে পেতাম, কিন্তু আমি যদি অসহযোগিতা করি তাহলে আমি পাবো আরো বেশী :৫০০ ডলার। এর উপসংহার হচ্ছে, আপনি যে কার্ডটি খেলুন না কেন, আমার সেরা চালটি হবে ‘সবসময়ই অসহযোগিতা করা।

সুতরাং আমি একটি নির্ভুল যুক্তি বের করেছি যে, আপনি যাই করুন কেন আমি অবশ্যই অসহযোগিতা করবো। এবং আপনিও কোনো অংশেই কম নির্ভুল নয় এমন যুক্তি দিয়ে ঠিক একই সিদ্ধান্ত নেবেন। সুতরাং যখন দুটি যুক্তিসম্পন্ন মানুষ মিলিত হয়, তারা দুজনেই অসহযোগিতার কার্ড খেলে, তারা দুজনেই হয় জরিমানার শাস্তি পায় অথবা কম পরিমান টাকা পায়। তারপরও দুজনেই খুব ভালো করে জানেন যে, যদি তারা দুজনে সহযোগিতা কার্ডটি খেলে থাকেন, তারা দুজনেই বেশ ভালো পরিমানে পুরষ্কার আদায় করতে পারতেন পারস্পরিক সহযোগিতার জন্য (আমাদের উদাহরণে, ৩০০ ডলার); একারণে এই খেলাটিকে বলে একটি ডাইলেমা বা উভয় সংকট, কেন এটি এত বেশী পাগল করে দেবার মত ধাঁধা সৃষ্টি করে এবং কেন এমনকি প্রস্তাব করা হয়েছে এর বিরুদ্ধে একটি আইন থাকা উচিৎ।

 ‘প্রিজনার’ শব্দটি এসেছে আরো একটি বিশেষ কাল্পনিক উদাহরণ থেকে। এখানে বিনিময় হচ্ছে টাকা নয় বরং জেলে থাকার শাস্তির পরিমান। দুইজন ব্যক্তি– তাদের নাম যেমন ধরুন, পিটারসন এবং মরিয়ার্টি– বর্তমানে কারাগারে আটক, পুলিশের সন্দেহ সহযোগীরূপে তারা দুইজন একটি অপরাধ সংঘটন করেছে। দুইজন অবস্থান করছে কারাগারের পৃথক দুটি কক্ষে, এবং পৃথকভাবেই তারা দুইজন পুলিশের জেরার মুখোমুখি হয়, দুইজনকেই আলাদা করে অপরাধের অপর সহযোগীর সাথে বিশ্বাসঘাতকতা (ডিফেক্ট) করতে, এবং রাজসাক্ষী হবার জন্য প্রস্তাব দেয়া হয়। যা ঘটে তা নির্ভর করবে এই দুইজন বন্দী কি করবে তার উপর, এবং কেউ জানেনা অন্যজন কি করেছে। যদি পিটারসন সব দোষ মরিয়ার্টির উপর চাপিয়ে দেয় এবং মরিয়ার্টি সেই কাহিনীটিকে সত্য হবার সম্ভাবনা বাড়িয়ে দেয় চুপ থাকার মাধ্যমে (তার একসময়কার বন্ধু এবং যে কিনা দেখা গেল বিশ্বাসঘাতক বন্ধু)। মরিয়ার্টি দীর্ঘ মেয়াদী শাস্তি পায়, অন্যদিকে পিটারসন কোন শাস্তি ছাড়াই জেল থেকে মুক্তি পায়, যে “ডিফেক্ট’ বা অসহযোগিতা আর বিশ্বাসঘাতকতা করার প্রলোভনের কাছে নতি স্বীকার করে। যদি তারা দুজনেই দুজনের সাথে বিশ্বাসঘাতকতা করতো, দুজনেই অপরাধের জন্য দোষী সাব্যস্ত হতো, কিন্তু আরেকজনের বিরুদ্ধে সাক্ষ্য দেবার মাধ্যমে অপরাধের কিছু প্রমাণ দেবার কারণে খানিকটা ছাড় পেতো, এবং যদিও কঠোর, তবে খানিকটা হ্রাসকৃত সাজায় দণ্ডিত হতো, পারস্পরিক বিশ্বাসঘাতকতার শাস্তি। যদি দুইজনই সহযোগিতা করতে ( একে অপরের সাথে, কর্তৃপক্ষের সাথে না), দুইজনের কেউ কোনো কিছু বলতে অস্বীকৃতি জানিয়ে, তাহলে তাদের মূল সেই অপরাধের জন্য সাজা দেবার জন্য কতৃপক্ষের হাতে যথেষ্ট পরিমান প্রমাণ ছিলনা। তারা বরং এর বদলে অপেক্ষাকৃত ছোট কোনো অপরাধের জন্য অল্প খানিকটা সাজা পেত, পারস্পরিক সহযোগিতার করার জন্য পুরষ্কার। যদিও, জেলখানার কোনো শাস্তিকে পুরষ্কার হিসাবে চিহ্নিত করা মনে হতে পারে বেশ অদ্ভুত একটি বিষয়, কিন্তু ঠিক সেভাবেই তারা সেটি দেখতো, যদি কারাগারে আরো দীর্ঘতর সময় আটক থাকা এর বিকল্প হতো। আপনি হয়তো লক্ষ করবেন, যদিও পে-অফ এখানে ডলারে হচ্ছে। না বরং কারাগারে বন্দী থাকার শাস্তি, কিন্তু খেলার অপরিহার্য বৈশিষ্ট্যগুলো সংরক্ষিত থাকে (পছন্দের ক্রমানুসারে চারটি আউটকাম বা ফলাফলের তালিকাটি লক্ষ করুন)। যদি আপনি আপনাকে প্রতিটি বন্দীর জায়গায় কল্পনা করেন, মনে করে নেন যে উভয়েই যৌক্তিক আত্মস্বার্থ রক্ষার জন্য প্ররোচিত হবে এবং যেহেতু জোট বাধার জন্য তারা পরস্পরের সাথে আগে কথা বলতে পারবে না, আমরা দেখবো অন্যের সাথে বিশ্বাসঘাতকতা করা ছাড়া কারোই কোনো উপায় নেই, যার ফলে দুজনেই কঠোর শাস্তি পাবে।

এই উভয় সংকট থেকে মুক্তি পাবার কি কোনো উপায় আছে? দুজন খেলোয়াড়ই জানেন যে তাদের প্রতিপক্ষ যাই করুক না কেন, তারা নিজেরা বিশ্বাসঘাতকতা বা অসহযোগিতা করার চেয়ে ভালো কিছু করতে পারবেন না। তারপরও দুজনের আরো যে বিষয়টি জানা আছে সেটি হচ্ছে, যদি তারা দুজনই পরস্পরকে সহযোগিতা করে, প্রত্যেকেই সুবিধাজনক একটি ফলাফল পাবে, শুধুমাত্র যদি, শুধুমাত্র যদি তারা সেটি করে .. শুধুমাত্র যদি তারা কোনো না কোনোভাবে ঐক্যমতে পৌঁছাতে পারতো, কোনো না কোনোভাবে দুজনই যদি একে অপরকে আশ্বস্ত করতে পারতো, তাদের কেউ বিশ্বাসঘাতকতা করে স্বার্থপরের মত ভালো পুরস্কারটি কেড়ে নেবে না, এবং কোনোভাবে যদি এই চুক্তির উপর নজরদারী করা তারা নিশ্চিৎ করতে পারতো।

প্রিজনার বা বন্দীদের এই উভয় সংকটের সরল খেলায়, এই পারস্পরিক বিশ্বাসকে নিশ্চিৎ করার কোনো উপায় নেই। যদি না কোনো একজন খেলোয়াড় সত্যিকারভাবে সাধুসদৃশ্য ‘সাকার’, যারা এই পৃথিবীর জন্য অতিরিক্ত ভালো, পুরো খেলাটা শেষ হবার সম্ভাবনা আছে পারস্পরিক বিশ্বাসঘাতকার মাধ্যমে, যা ফলাফল কাঙ্খিত ফলাফলের বিপরীত, দুজনের জন্য যা খারাপ পরিণতির কারণ হবে। কিন্তু এই খেলাটার আরো একটি সংস্করণ আছে। এটিকে বলে ‘পুনরাবৃত্তি হওয়া বন্দীদের উভয়সংকট বা আইটিরেটেড অথবা রিপিটেড প্রিজনার’স ডাইলেমা। পুনরাবৃত্তি হওয়া খেলাটি আরো বেশী জটিল এবং এই জটিলতার মধ্যেই আছে আশা।

এই ‘পুনরাবৃত্তি হওয়া খেলাটি খুবই সাধারণ সেই একই খেলার মত, শুধুমাত্র যেটি একই খেলোয়াড়দের নিয়ে অনির্দিষ্টবারের জন্য পুনরাবৃত্তি হয়। আরো একবার আমি এবং আপনি মুখোমুখি হই, আমাদের মাঝে বসে থাকেন মিমাংসাকারী ব্যাঙ্কার। আবারো আমাদের হাতে দুটো করে কার্ড থাকে, একটি সহযোগিতা, আর আরেকটি অসহযোগিতা/বিশ্বাসঘাতকতা বা কোঅপারেট এবং ডিফেক্ট। আবারো খেলার দানে আমাদের দুজন এই দুটি কার্ডের যেকোনো একটি খেলবো, এবং উপরে বর্ণিত সেই খেলার নিয়মানুযায়ী ব্যাঙ্কার হয় টাকা দেবে, নয়তো জরিমানার শাস্তি প্রদান করবে। কিন্তু এখন, সেই খেলাটি একবার শেষ হবার বদলে, আমরা আবারও কার্ড হাতে তুলে নিয়ে নতুন খেলার দান শুরু করি। এভাবে একের পর এক খেলার চক্র আমাদের সুযোগ দেয় বিশ্বাস অথবা অবিশ্বাস সৃষ্টি করার জন্য, একে অপরের কাজের প্রতিদান অথবা তোষণ বা ক্ষমা বা প্রতিশোধ নেয়ার। একটি অনির্দিষ্ট সময়ব্যাপী চলমান দীর্ঘ খেলায়, সবচেয়ে গুরুত্বপূর্ণ ব্যপারটি হচ্ছে, আমরা দুজনেই জিততে পারি ব্যাঙ্কারকে বোকা বানিয়ে, নিজেদের কোনো ক্ষতি না করে।

এভাবে এই খেলার দশ রাউন্ড পর, তাত্ত্বিকভাবে আমি প্রায় ৫০০০ ডলার জয় করতে পারি, কিন্তু শুধুমাত্র যদি আপনি খুব বড় মাপের বোকা হয়ে থাকেন (বা মহাপুরুষ সাধুসুলভ হন) এবং সবসময়ই সহযোগিতার কার্ডটি খেলে থাকেন, এমনকি যখন আমি সবসময়ই অসহযোগিতার কার্ডটি খেলে যাচ্ছি। আরো বাস্তবসম্মতভাবে, আমাদের দুজনের জন্যই খুব সহজ হবে ব্যাঙ্কারের ৩০০০ ডলার হাতিয়ে নেয়া এই খেলার দশটির রাউন্ডের প্রতিটিতে দুজনেই সহযোগিতার কার্ডটি খেলে। এর জন্য আমাদের বিশেষভাবে সাধুসুলভ হতে হবে না, কারণ আমরা দুজনেই দেখতে পাচ্ছি, একে অপরের অতীতের দান থেকে, পরস্পরকে আমরা বিশ্বাস করতে পারবো। আমরা কার্যত একে অপরের আচরণের উপর নজরদারী করতে পারবো। আরেকটা বিষয় হচ্ছে, এমনও সম্ভাবনা আছে। আমাদের কেউ একে অপরকে বিশ্বাস করতে পারবো না। আমরা দুজনেই ডিফেক্ট অসহযোগিতার কার্ডটি খেলছি পুরো দশ রাউন্ড জুড়ে এবং ব্যাঙ্কার আমাদের প্রত্যেকের কাছ থেকে ১০০ ডলার জরিমানা আদায় করে নেবেন। খুব সম্ভবত যেটা হবে আমরা একে অপরকে আংশিকভাবে বিশ্বাস করবো, এবং আমরা দুজনেই সহযোগিতা আর অসহযোগিতার একটি মিশ্র’ কৌশল ধারাবাহিকভাবে খেলে যাবো, মোটামুটি মাঝারী পরিমান টাকা আদায় করা সম্ভব হবে।

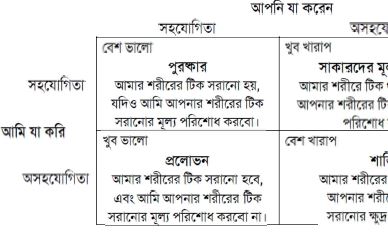
 অধ্যায় ১০ এর পাখিরা যারা একে অপরের মাথার উপরের পালক থেকে ছোট কীট বা টিক অপসারণ করতে সাহায্য করে তারাও একধরনের বহুবার পুনরাবৃত্তি হওয়া প্রিজনার’স ডাইলেমা বা উভয়সঙ্কট খেলাটি খেলে। কিভাবে তারা সেটি খেলে? আপনার নিশ্চয়ই মনে আছে কোনো একটি পাখির পক্ষে তার নিজের পালক থেকে টিক অপসারণ করাটা জরুরী একটি ব্যাপার, কিন্তু সে তার নিজের মাথার উপরের জায়গাটি নিজে ঠোঁট দিয়ে খুটে পরিষ্কার করতে পারেনা, তার তখন অন্য সঙ্গীর দরকার হয়, যে সেই কাজটি তার হয়ে করে দেয়। এখানে স্পষ্টতই মনে হতে পারে খুব স্বাভাবিক ব্যপারটি হবে, সে পরে তার সঙ্গীর করা এই উপকারটির অবশ্যই প্রতিদান দেবে। কিন্তু এই প্রতিদান দিতে হলে পাখি হিসাবে তার সময় ও শক্তির খরচ হবে, যদিও খুব বেশী নয়। যদি কোনো পাখি, প্রতিদান না দিয়ে বা প্রতারণা করে পার পেয়ে যেতে পারে– মানে তার নিজের মাথার টিক পরিষ্কার করার পর, প্রতিদান দিতে অস্বীকার করে– সে মূল্য পরিশোধ না করেই লাভবান আউটকাম বা পরিণতিগুলোকে যদি আপনি পর্যায়ক্রমে সাজান এবং আপনি দেখবেন সত্যিকারের একটি প্রিজনার’স ডাইলেমা গেমই এখানে খেলা হচ্ছে। উভয়পক্ষই যেখানে সহযোগিতা করছে (একে অপরের মাথাকে টিক তুলে দেয়া) সেখানে পরিস্থিতি বেশ ভালো, কিন্তু তারপরও কোনো প্রতিদান ছাড়াই বা কোনো মূল্য পরিশোধ না। করেই উপকার নেবার মাধ্যমে আরো বেশী লাভ করার প্রলোভনও আছে।

দুজনেই অসহযোগিতা করলে (একে অপরের মাথা থেকে টিক পরিষ্কার করতে অস্বীকার করলে) পরিস্থিতি দুজনের জন্যেই বেশ খারাপ হয়। কিন্তু এতটা খারাপ হয় না যেমন হতে পারে যখন কষ্ট করে কারো মাথা থেকে টিক পরিষ্কার করার পরেও নিজের শরীর টিক দ্বারা আক্রান্ত থেকে যায়। লাভ-ক্ষতির হিসাবের ছকটি আমরা দেখতে পারে ছবি ২ তে।

 কিন্তু এটি শুধুমাত্র একটি উদাহরণ। আপনি বিষয়টি নিয়ে যত ভাববেন, তত বেশী আপনি অনুধাবন করতে পারবেন জীবন পূর্ণ হয়ে আছে বহুবার পুনরাবৃত্তি হওয়া প্রিজনার’স ডাইলেমা খেলায়, শুধু মানুষের জীবন না বরং প্রাণী এবং উদ্ভিদের জীবনেও। উদ্ভিদের জীবন? হ্যাঁ, কেন নয়? মনে রাখবেন আমরা সচেতনতার স্তরে নেয়া হয়েছে এমন কোনো সিদ্ধান্তের কথা বলছি না (যদিও মাঝে মাঝে আমরা সেটা করতে পারি), এই কৌশলগুলো আসলেই ‘মেনার্ড স্মিথের প্রস্তাবিত অর্থে’, সেই সব কৌশল জিনরা হয়তো যা আগে থেকেই প্রোগ্রাম করতে পারে। পরে আমরা কিছু উদ্ভিদ দেখবো, বেশ কিছু প্রাণী এবং এমনকি ব্যাকটেরিয়া, সবাই এই পুনরাবৃত্তি হতে থাকা প্রিজনার’স ডাইলেমা খেলাটি খেলছে। এখন তাহলে আসুন এই পুনরাবৃত্তি হবার বিষয়টি আসলেই কেন এত বেশী গুরুত্বপূর্ণ সেটি আরো গভীরভাবে অনুসন্ধান করার চেষ্টা করি।

সাধারণ খেলার চেয়ে, যেখানে বরং আগে থেকেই ধারণা করা যেতে পারে, ‘অসহযোগিতা হচ্ছে একমাত্র ‘যৌক্তিক’ কৌশল। এই পুনরাবৃত্তি হওয়া সংস্করণটি খেলোয়াড়দের বহু সংখ্যক কৌশল ব্যবহার করার সুযোগ দেয়। সাধারণ খেলায় শুধুমাত্র দুটি সম্ভাব্য কৌশল আছে: “সহযোগিতা এবং অসহযোগিতা। তবে পুনরাবৃত্তি, যদিও বহু সংখ্যক সম্ভাব্য কৌশলের সুযোগ করে দেয়, কিন্তু তাদের মধ্যে কোনটি সবচেয়ে সেরা কোনোভাবেই সেটি সুস্পষ্ট নয়। নীচে, যেমন, হাজারটি কৌশলের একটি: ‘বেশীরভাগ সময় সহযোগিতা করো, কিন্তু ১০ শতাংশ সময় র‍্যানডোমভাবে বিশ্বাসঘাতকতার খেলা খেল; অথবা কৌশল হতে পারে খেলার অতীত ইতিহাসের উপর শর্তাধীন। আমার গ্রাজার’ হচ্ছে এই ধরনের একটি উদাহরণ, কে কেমন এ বিষয়ে তাদের খুব ভালো স্মৃতি আছে এবং যদিও মৌলিকভাবে তারা পরস্পরের সহযোগিতা করে, তবে তারা বিশ্বাসঘাতকতা করে, যদি অন্য খেলোয়াড় এর আগে কখনো বিশ্বাসঘাতকতা করে থাকে। অন্য কোনো কৌশল হয়তো আরো বেশী ক্ষমাশীল হবে, অপেক্ষাকৃত স্বল্প মেয়াদী স্মৃতির জন্য।

স্পষ্টতই পুনরাবৃত্তির খেলায় অনেক কৌশল আছে, শুধুমাত্র আমাদের উদ্ভাবনপটুতাই যার সীমাবদ্ধতা। আমরা কীভাবে কোনটি সবচেয়ে সেরা, সেটি চিহ্নিত করতে পারি? অ্যাক্সেলরড নিজেই এই কাজটি করতে উদ্যোগী হয়েছিলেন। একটি প্রতিযোগিতার আয়োজন করার মত বেশ চমকপ্রদ একটি ধারণা হয়েছিল তার, তিনি ‘গেম-থিওরী’ বিশেষজ্ঞদের কাছে তাদের সেরা কৌশলগুলো জমা দেবার জন্যে বিজ্ঞাপন দিয়েছিলেন। কৌশল, এই অর্থে, কোনো কাজ করার পূর্বনির্ধারিত প্রোগ্রাম করা নিয়মকানুন, সুতরাং প্রতিযোগীদের জন্যে প্রযোজ্য ছিল যে, তাদের কৌশলগুলো কম্পিউটার প্রোগ্রামের ভাষায় জমা দিতে হবে। মোট চৌদ্দটি কৌশল জমা পড়েছিল, অ্যাক্সেলরড এর সাথে পনেরোতমটি যোগ করেন, যার নাম দেন ‘র্যানডোম’, যা এলোমেলোভাবে কোনো সুনির্দিষ্ট নিয়ম না মেনেই শুধুমাত্র সহযোগিতা’ আর ‘অসহযোগিতা কার্ডটি খেলে যায় এবং এটাকে ধরে নেয়া হয়েছে এক ধরনের বেস লাইন বা শুরুর ‘নন-স্ট্র্যাটেজী’ হিসাবে, যদি কোনো কৌশল এই ‘র্যানডোম’ কৌশলের চেয়ে ভালো না করে, এটি অবশ্যই যথেষ্ট খারাপ একটি কৌশল।

অ্যাক্সেলরড ১৫ টি কৌশলকেই অনুবাদ করেছিলেন একটি সাধারণ প্রোগ্রামিং-এর ভাষায় এবং এরপর এটিকে একটি বড় কম্পিউটারে ‘পুনরাবৃত্তি হওয়া প্রিজনার’স ডাইলেমা’ খেলার মাধ্যমে পরস্পরের সাথে প্রতিদ্বন্দ্বিতা করার সুযোগ করে দিয়েছিলেন (তার নিজের একটি কপির সাথেও)। যেহেতু ১৫ টি কৌশল ছিল, সুতরাং ১৫x১৫ বা ২২৫টি ভিন্ন ভিন্ন খেলা কম্পিউটারে চলেছিল। যখন প্রতিটি জোড়া খেলা মোট ২০০টি দান অতিক্রম করেছিল, মোট লভ্যাংশ যোগ করে বিজয়ী ঘোষণা করা হয়েছিল।

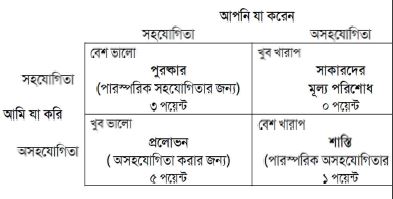
একটি বিশেষ প্রতিপক্ষের সাথে যুদ্ধে কোন কৌশলটি জয়লাভ করেছে তা নিয়ে আমরা আদৌ চিন্তিত নই। যা আমাদের চিন্তার বিষয় সেটি হচ্ছে কোন কৌশলটি সবচেয়ে বেশী পরিমান টাকা সঞ্চয় করতে পারে, যদি পনেরো জোড়ার সব কৌশল আমরা যোগ করি। টাকা মানে এখানে শুধু পয়েন্টস বা নম্বর যা বরাদ্দ করা হয়েছে। এভাবে: পরস্পর সহযোগিতা, ৩ পয়েন্ট, অসহযোগিতা করার প্রলোভন, ৫ পয়েন্ট, পারস্পরিক অসহযোগিতার জন্য ১ পয়েন্ট ( যা আগের খেলার মৃদু জরিমানার সমান), সাকারদের মূল্য পরিশোধ, ০ পয়েন্ট (যা আমাদের আগের খেলার বেশী পরিমান জরিমানার সমতুল্য)।

সম্ভাব্য সর্বোচ্চ স্কোর যা কোনো একটি কৌশল অর্জন করতে পারে তাহলো ১৫,০০০ (২০০ রাউন্ড এবং প্রতি রাউন্ডে ৫ পয়েন্ট, ১৫ জন প্রতিপক্ষ, প্রত্যেকের জন্য)। সর্বনিম্ন সম্ভাব্য স্কোর হচ্ছে ০; বলার অপেক্ষা রাখেনা এই দুটি চরম সীমার কোনোটাই ঘটে না। বাস্তবসম্মতভাবে কোনো একটি কৌশল যা অর্জন করার আশা করতে পারে, সেটি হচ্ছে গড়ে যেকোনো ১৫টি জোড়ায় সেটি ৬০০ এর খুব একটা বেশী হতে পারেনা। এটাই দুইজন খেলোয়াড় প্রত্যেকে অর্জন করে, যদি তারা সবসময়ই সহযোগিতা করে একে অপরের সাথে, খেলার প্রতিটি ২০০ রাউন্ডের জন্য ৩ পয়েন্ট করে পাবার মাধ্যমে। যদি দুজনের কেউ বিশ্বাসঘাতকতার প্রলোভনের শিকার হয়, তারা খুব সম্ভবত ৬০০ এর কম বেশী পয়েন্ট অর্জন করতে পারে কারণ অন্য খেলোয়াড় তাদের বিশ্বাসঘাতকতার বদলা নেয় (বেশীর ভাগ কৌশলের মধ্যেই কোনো ধরনের বিশ্বাসঘাতকার বিরুদ্ধে পাল্টা ব্যবস্থা নেবার বিষয়টি সংশ্লিষ্ট থাকে)। আমরা এই ৬০০ পয়েন্টকে ব্যবহার করতে পারি খেলার একধরনের বেঞ্চমার্ক হিসাবে এবং সব ফলাফলই আমরা বেঞ্চমার্কের একটি শতকরা সংখ্যা হিসাবে চিহ্নিত করতে পারি। এই মাত্রায় তাত্ত্বিকভাবে ১৬৬ শতাংশ অর্জন করা সম্ভব (১০০০ পয়েন্ট) কিন্তু বাস্তবে কোনো কৌশলের গড় স্কোর ৬০০ অতিক্রম করেনা।

মনে করে দেখুন, এই প্রতিযোগিতায় ‘খেলোয়াড়রা’ কিন্তু মানুষ নয় বরং কম্পিউটার প্রোগ্রাম, পূর্বে প্রোগ্রাম করা কৌশল। তাদের মানব লেখকরা, শরীরে প্রোগ্রাম করতে জিনরা যে দ্বায়িত্ব পালন করে, ঠিক সেই একই দ্বায়িত্ব পালন করেছেন ( চিন্তা করুন অধ্যায় ৪ এর কম্পিউটার দাবা এবং অ্যান্ড্রোমিডা কম্পিউটারের কথা); আপনি এই কৌশলটাকে তাদের লেখকদের কাছে ছোট আকারের প্রক্সির মত ভাবতে পারেন। আসলেই, একজন লেখক একটি কৌশলের বেশী আরো বেশী কৌশল জমা দিতে পারতেন (যদিও সেটি হতো প্রতারণা– এবং অ্যাক্সেলরড খুব সম্ভবত প্রতিযোগিতায় কোনো একটি লেখককে একাধিক কৌশল প্রয়োগ করার অনুমতি দিতেন না, যাদের একটি হয়তো অন্যদের সত্যিকারের আত্মত্যাগী সহযোগিতার বিনিময়ে সুবিধা ভোগ করতো)।

কিছু উদ্ভাবনী কৌশলও খেলায় জমা দেয়া হয়েছিল, যদিও তারা অভিনব, তবে তাদের লেখকদের চেয়ে অবশ্যই অনেক কম উদ্ভাবনপটু। বিজয়ী কৌশলটি, উল্লেখযোগ্যভাবে, ছিল সবচেয়ে সরলতম এবং উপরিদৃষ্টিতে সবচেয়ে কম উদ্ভাবনী। এর নাম হচ্ছে ‘টিট ফর ট্যাট’ (হ্যাঁ, সেই ইটের বদলে পাটকেল), এটি জমা দিয়েছিলেন অধ্যাপক আনাতোল র‍্যাপোপোর্ট, টরোন্টোর একজন বিখ্যাত মনোবিজ্ঞানী এবং গেম থিওরিস্ট। টিট ফর ট্যাট’ শুরু হয় প্রথম দানে সহযোগিতা করার মাধ্যমে এবং এরপরে শুধু অন্য খেলোয়াড় এর আগে যে দানটি খেলবে সেটারই পুনরাবৃত্তি করে যায়।

কোনো একটি ‘টিট ফর ট্যাট’ কৌশলসহ গেম কিভাবে অগ্রসর হবে? যেমন হয় সবসময়, যা ঘটে তা নির্ভর করে অন্য খেলোয়াড়দের উপর। ধরুন, প্রথম, অন্য খেলোয়াড়ও ‘টিট ফর। ট্যাট’ (মনে রাখবেন প্রতিটি কৌশল তার নিজের অনুলিপির সাথে খেলবে, যেমন, অন্য ১৪টি কৌশলের সাথে খেলে); উভয় ‘টিট ফর ট্যাট’ সহযোগিতার মাধ্যমে খেলা শুরু করে, এর পরের দানে, প্রতিটি খেলোয়াড় তাদের আগের দানকে ‘কপি করে, সেটি হচ্ছে ‘সহযোগিতা। এভাবে দুজনই সহযোগিতা করে যায় খেলার শেষ হওয়া অবধি এবং উভয়ই বেঞ্চমার্ক স্কোর ৬০০ পয়েন্টের পুরো ১০০ শতাংশ পয়েন্ট অর্জন করে।

এখন মনে করুন, ‘টিট ফর ট্যাট’ একটি কৌশলের বিরুদ্ধে খেলছে যার নাম নেইভ প্রোবার’, ‘নেইভ প্রোবার’ আসলে অ্যাক্সেলরডের প্রতিযোগিতা অংশ নেবার জন্য জমা দেয়া হয়নি, কিন্তু তাসত্ত্বেও এটি বিশেষ শিক্ষণীয়। এটি মূলত হুবহু ‘টিট ফর ট্যাট’-এর মত, শুধুমাত্র, কখনো, ধরুন রানডোমভাবে প্রতি দশ দানে একবার সে মূল্য পরিশোধ না করে বিশ্বাসঘাতকতার দান খেলে এবং প্রলোভনের জন্য বেশী পয়েন্ট দাবী করে। যতক্ষণ না অবধি ‘নেইভ প্রোবার’ তার কোনো একটি প্রোবিং’ (অনুসন্ধানী অসহযোগিতার দান না খেলে, খেলোয়াড়দের দুটি ‘টিট ফর ট্যাট’ বলা যেতে পারে। কিন্তু হঠাৎ করে, কোনো সতর্কবাণী ছাড়া, ধরুন অষ্টম দানে, ‘নেইভ প্রোবার বিশ্বাসঘাতকতা করে। টিট ফর ট্যাট, অবশ্যই, সহযোগিতার দান চেলেছিলো এই দানে, সুতরাং সে ‘সাকারদের হিসাব অনুযায়ী ০ পয়েন্ট পায়। নেইভ প্রোবার’ আপাতদৃষ্টিতে খুবই ভালো করছিল, কারণ ততক্ষণে এটি সেই দান থেকে ৫ পয়েন্ট পেয়েছে, কিন্তু এর পরের দানে ‘টিট ফর ট্যাট’, ‘বদলা’ নেয়। এটি অসহযোগিতার কার্ড খেলে, সরলভাবে সে তার প্রতিপক্ষের আগের দানটির পুনরাবৃত্তি করে। নেইভ প্রোবার’ ইতিমধ্যে, অন্ধভাবে তার ভিতরের অনুলিপি করার নিয়মটি মেনে চলে, এবং প্রতিপক্ষের সহযোগিতার দানটি অনুলিপি করে। সুতরায় এটি এখন সাকারদের পেঅফ, ০ পয়েন্ট অর্জন করে, অন্যদিকে টিট ফর ট্যাট ৫ পয়েন্ট পায়। এর পরের দানে, নেইভ প্রোবার-বলা যায় খানিকটা অনায্যভাবেই– টিট ফর ট্যাট এর অসহযোগিতার বিরুদ্ধে বদলা নেয়। এবং এভাবেই দানে একান্তর পরিবর্তনটি ঘটে। এই রদবদলগুলোর সময় দুই খেলোয়াড়ই ২.৫ পয়েন্ট পায় প্রতিটি দানে (৫ এবং ০র গড়)। এটি স্থিতিশীল ৩ পয়েন্ট অপেক্ষা কম প্রতিদানে যা খেলোয়াড়রা জমা করতে পারে পারস্পরিক সহায়তার মাধ্যমে ( এবং, যাই হোক, এটাই কারণ, বাড়তি শর্তাবলীর জন্য, যা ব্যাখ্যা করা হয়নি মূল বইয়ের পৃষ্ঠা ২৬৪ এ); সুতরাং, যখন ‘নেইভ প্রোবার’ ‘টিট ফর ট্যাটের বিরুদ্ধে খেলে, তারা দুজনেই খারাপ করে, কোনো ‘টিট ফর ট্যাট’ আরেকজন টিট ফর ট্যাটের বিরুদ্ধে খেললে যা অর্জন করে তার তুলনায়। এবং যখন কোনো ‘নেইভ প্রোবার’ আরেকজন ‘নেইভ প্রোবার’-এর সাথে খেলে, তাদের প্রবণতা থাকে, আর যাই হোক না কেন, এমনকি আরো খারাপ করার, কারণ পুনরাবৃত্তি হওয়া অসহযোগিতার দানগুলো আরো আগেই শুরু হবে।

এবার আরো একটি কৌশলের কথা ভাবুন, রিমোর্সফুল প্রোবার। রিমোর্সফুল প্রোবার, নেইভ পোবারদের মত, শুধুমাত্র এটি সক্রিয় পদক্ষেপ নেয় একান্তরভাবে ফিরে আসা পারস্পরিক অভিযোগের বলয় থেকে বের হয়ে আসতে। এটা করতে তার প্রয়োজন খানিকটা দীর্ঘ স্মৃতি, যা ‘টিট ফর ট্যাট’ অথবা ‘নেইভ প্রোবার’ থেকে দীর্ঘ। ‘রিমোর্সফুল প্রোবার’ মনে রাখে এটি শুধুমাত্র স্বতস্ফূর্তভাবে অসহযোগিতা করেছে কিনা অথবা ফলাফল হচ্ছে দ্রুত বদলা। যদি তাই হয়, এটি “অনুশোচনার সাথে তার প্রতিপক্ষকে কোনো ধরণের পাল্টা বদলা ছাড়া একটি ফ্রি হিট’ বা সুযোগের অনুমতি দেয়। এর মানে হলো যে, পারস্পরিক দোষারোপের দানগুলো শুরুতেই বিনষ্ট হয়। এবার যদি আপনি ‘রিমোর্সফুল প্রোবার’ আর ‘টিট ফর ট্যাটের’ সেই কাল্পনিক খেলায় দানগুলো পর্যালোচনা করেন, তাহলে আপনি দেখবেন যে, সম্ভাব্য পারস্পরিক বদলার প্রতিটি দান দ্রুত বন্ধ করা হয়। বেশীর ভাগ খেলাই অতিক্রান্ত হয় পারস্পরিক সহযোগিতার মাধ্যমে, যেখানে উভয় খেলোয়াড়ই এর পরিণতিতে বেশ ভালো পরিমান স্কোর অর্জন করে। রিমোর্সফুল প্রোবার’ ‘টিট ফর ট্যাটের বিরুদ্ধে ভালো খেলে ‘নেইভ প্রোবার’ এর চেয়ে, যদিও ‘টিট ফর ট্যাট’ নিজের বিরুদ্ধে যা করে তারচেয়ে বেশী ভালো করে না।

অ্যাক্সেলরডের প্রতিযোগিতায় কিছু কৌশল, যাদের জমা দেয়া হয়েছিল, সেগুলো রিমোর্সফুল অথবা নেইভ প্রোবার দুজনের যে কোনোটির চেয়ে অনেক বেশী জটিল, কিন্তু তারাও অল্প কিছু পয়েন্ট পায়, গড় হিসাবে, সরল টিট ফর ট্যাট এর তুলনায়। আসলেই সবচেয়ে কম সফল এই সব কৌশলের মধ্যে (ব্ল্যানডোম ছাড়া) সেটি সবচেয়ে বেশী বিস্তারিত। এটি জমা দিয়েছিলেন “নাম উল্লেখ করতে অনিচ্ছুক একজন’– এ বিষয়ে মজার কিছু কল্পনা করার জন্য যা সহায়ক, পেন্টাগনের কোনো ‘এমিনন্স গ্রিজ’ বা পর্দার আড়ালে কলকাঠি নাড়ানো শক্তিশালী কেউ? সিআইএ’র প্রধান? হেনরী কিসিঞ্জার? অ্যাক্সেলরড নিজে? আমার মনে করি আমরা কোনদিনও সেটা জানতে পারবো না।

যে সব কৌশলগুলো প্রতিযোগিতার জন্য জমা করা হয়েছিল, সেগুলোর প্রত্যেকটির নির্দিষ্ট কৌশল পরীক্ষা করে দেখার কোনো প্রয়োজন নেই এবং সেটি সুপাঠ্য হবেনা, কারণ এই বইটি কম্পিউটার প্রোগ্রামদের দক্ষতা সংক্রান্ত কোনো বই নয়। বরং আরো বেশী গুরুত্বপূর্ণ হবে কৌশলগুলো শ্রেণীভুক্ত করা এবং এইসব অপেক্ষাকৃত বড় শ্রেণীগুলোর সফলতা নীরিক্ষা করে দেখা। অ্যাক্সেলরড যে কৌশলটিকে সবচেয়ে গুরুত্বপূর্ণ হিসাবে চিহ্নিত করেছিলেন সেটি হচ্ছে ‘নাইস। নাইস’ কৌশল হচ্ছে সেটি যা কখনোই প্রথমে নিজে ‘অসহযোগিতা করবে না। টিট ফর ট্যাট’ এর একটি উদাহরণ। এটি ‘অসহযোগিতা করতে পারে, কিন্তু সে ‘বদলা নিতে এটি করবে। নেইভ প্রোবার’ এবং ‘রিমোসফুল প্রোবার হচ্ছে বাজে কৌশল কারণ, তারা মাঝে মাঝে ‘বিশ্বাসঘাতকতা বা অসহযোগিতা করে, যদিও কদাচিৎ, যখন সেটি করার জন্য তাদের প্ররোচিত করা হয়না। ১৫ টি কৌশলের মধ্যে, যারা অ্যাক্সেলরডের প্রতিযোগিতায় অংশ নিয়েছিল, ৮ টি ছিল ‘নাইস’। উল্লেখযোগ্যভাবে যে ৮ টি কৌশল সবচেয়ে বেশী পয়েন্ট সংগ্রহ করেছিল তারা এই একই ৮ টি কৌশল, বাকী ৭ টি খারাপ কৌশল পয়েন্ট সংগ্রহে এর অনুসরণ করে। টিট ফর ট্যাট’ গড়ে অর্জন করে ৫০৪.৫ পয়েন্ট, বেঞ্চমার্ক পয়েন্ট ৬০০ র ৮৪ শতাংশ এবং একটি ভালো স্কোর। অন্য ‘নাইস’ কৌশলগুলো খানিকটা কম নম্বর পায়, যাদের স্কোর ৮৩.৪ শতাংশ খেকে ৭৮.৬ শতাংশ। একটি বড় পার্থক্য আছে এই স্কোরের বিস্তারে, এবং ৬৬.৮ শতাংশ যা অর্জন করেছিল ‘গ্রাসক্যাম্প’ কৌশলটি, সব ‘ন্যাস্টি’ বা খারাপ কৌশলের মধ্যে যেটি সবচেয়ে বেশী পয়েন্ট অর্জন করেছিল। সুতরাং দেখে বেশ বিশ্বাসযোগ্য মনে হয় যে একটি বাস্তব সত্য হচ্ছে, খেলায় ‘নাইস’ খেলোয়াড়রা বেশ ভালো করে।

অ্যাক্সেলরডের আরেকটি কারিগরী শব্দ হচ্ছে ‘ফরগিভিং’ বা ক্ষমাশীল। ফরগিভিং স্ট্রাটেজী হচ্ছে সেটি, যদিও হয়তো সে বদলা নেয়, তবে এর স্মৃতি বেশী দীর্ঘ নয়। পুরোনো কোনো বিশ্বাসঘাতকতাকে সে খুব দ্রুত ভুলে যায়। টিট ফর ট্যাট’ এমন একটি ‘ফরগিভিং’ (বা ক্ষমাশীল) কৌশল। কোনো বিশ্বাসঘাতককে সে তাৎক্ষণিকভাবে শাস্তি দেয়, তবে যা হয়ে গেছে, সেটাকে সে অতীতের ঘটনা হিসাবে ভুলে যায়। অধ্যায় ১০ এর ‘গ্রাজার’রা পুরোপুরিভাবে কখনোই ক্ষমা করেনা। পুরো খেলা জুড়ে তার স্মৃতি অটুট থাকে। তার সাথে এমনকি একবার মাত্র বিশ্বাসঘাতকতা করেছে এমন কোনো খেলোয়াড়কে সে কখনোই ক্ষমা করেনা, তার বদলা নেবার ইচ্ছা অটুট থাকে। একটি কৌশল যা আনুষ্ঠানিকভাবে গ্রাজারদের মত, যা অ্যাক্সেলরডর প্রতিযোগিতায় অংশ নিয়েছিল। ‘ফ্রিডম্যান’ নামের অধীনে, এবং এটি বেশী ভালো করেনি। সবগুলো ‘নাইস’ কৌশলের মধ্যে ( লক্ষ করুন এটি হচ্ছে টেকনিকালী ‘নাইস’, যদিও পুরোপুরি ক্ষমাশীল নয়) গ্রাজার/ফ্রিডম্যান প্রায় সবচেয়ে খারাপ ফলাফল করেছে); ক্ষমাহীন স্ট্রাটেজীগুলোর বেশী ভালো করেনি তার কারণ হচ্ছে তারা পারস্পরিক বদলার নেবার চক্র থেকে বের হতে পারেনা, এমনকি যখন প্রতিপক্ষ ‘অনুশোচনাপূর্ণ।

 ‘টিট ফর ট্যাট’ এর চেয়েও ক্ষমাশীল হওয়া সম্ভব। টিট ফর টু ট্যাট’ অবশেষে বদলা নেবার আগে এর প্রতিপক্ষকে দুইবার বিশ্বাসঘাতকতা করার সুযোগ দেয়, এটি মনে হতে পারে বেশী মাত্রায় সাধুসুলভ মহত্বপূর্ণ আচরণ, যাই হোক অ্যাক্সেলর হিসাব করেছিলেন যে, যদি কেউ শুধুমাত্র ‘টিট ফর টু ট্যাট’ কৌশল জমা দিতো, এটি প্রতিযোগিতায় জয় লাভ করতে। কারণ এটি অত্যন্ত ভালো পারস্পরিক দোষারোপ আর বদলা নেবার চক্রটিকে এড়ানোর ক্ষেত্রে। সুতরাং আমরা দুটি বৈশিষ্ট্যকে চিহ্নিত করেছি জয়ী কৌশল হিসাবে: ‘নাইসনেস’ এবং ‘ফরগিভনেস’.. ভালোত্ব এবং ক্ষমাশীলতা। প্রায় অবিশ্বাস্য ইউটোপিয়ান-সদৃশ একটি উপসংহার– ভালোত্ব এবং ক্ষমাশীলতা লাভজনক– বহু বিশেষজ্ঞের কাছে এ ধরনের ফলাফল বিস্ময়কর মনে হয়েছিল, যারা খুব ধূর্ততার সাথে। সূক্ষ্মভাবে ‘ন্যাস্টি’ বা স্বার্থপর কৌশল জমা দেবার চেষ্টা করেছিলেন, এমনকি যারা নাইস কৌশলগুলো জমা দিয়েছিলেন, তারাও ‘টিট ফর টু ট্যাট’ এর মত এমন কোনো ক্ষমাসুলভ স্ট্রাটেজি জমা দেবার জন্য সাহস করেননি।

অ্যাক্সেলরড দ্বিতীয় একটি প্রতিযোগিতার ঘোষণা দিয়েছিলেন এরপর। প্রতিযোগিতায় অংশগ্রহনের জন্য তিনি মোট ৬২ টি কৌশল পান। এবং আবারো রানোম একটি কৌশল তিনি যোগ করেন, সুতরাং মোট অংশগ্রহনকারী প্রোগ্রামের সংখ্যা হয় ৬৩; এবার, খেলা প্রতি দান সংখ্যা তিনি ২০০ তে স্থির না করে উন্মুক্ত রাখেন একটি সঙ্গত কারণে, বিষয়টি আমি পরে আলোচনায় আনবো। আমরা এখনও স্কোরগুলো ‘বেঞ্চ মার্কের’ অথবা ‘সবসময় সহযোগিতা স্কোরের শতকরা হিসাবে প্রকাশ করবো, এমনকি যদি বেঞ্চমার্কের জন্য প্রয়োজন আরো জটিল গণনা এবং আর সুনির্দিষ্ট ৬০০ পয়েন্টের বেঞ্চমার্কের আর দরকার নেই।

দ্বিতীয় প্রতিযোগিতায় প্রোগ্রামারদের সবাইকে প্রথম প্রতিযোগিতার ফলাফল জানানো হয়েছিল, সেই অ্যাক্সেলরডের বিশ্লেষণ কেন ‘টিট ফর ট্যাট’ এবং অন্যান্য ভালো বা ‘নাইস’ ও ‘ক্ষমাসুলভ স্ট্রাটেজীগুলো এত ভালো ফলাফল করেছিল। শুধুমাত্র প্রত্যাশা করা হয়েছিল যে প্রতিযোগিরা এইসব পূর্বে পাওয়া তথ্যগুলো কোনো না কোনো একটি উপায়ে তাদের চিন্তায় আনবেন। বাস্তবিকভাবে, সেগুলো দুটি ভিন্ন চিন্তার ধারায় বিভক্ত। কেউ কেউ যুক্তি দিলেন ভালো এবং ক্ষমাশীলতা স্পষ্টতই বিজয়ী হবার কৌশল এবং সেভাবেই তারা ভালো আর ক্ষমাসুলভ কৌশলও জমা দিয়েছিলেন। জন মেনার্ড স্মিথ এমনকি অতি ক্ষমাশীল ‘টিট ফর টু ট্যাট’ জমা দিয়েছিলেন। অন্য চিন্তাটি যুক্তি দিয়েছিল যে তাদের অনেক সহকর্মী, অ্যাক্সেলরডের বিশ্লেষণ পড়ে এখন ভালো, ক্ষমাশীল কৌশল জমা দেবেন। সেকারণে এই সব নরম মনের প্রোগ্রামগুলোকে নিজেদের স্বার্থে ব্যবহার করার প্রচেষ্টায় তারা স্বার্থপর স্ট্র্যাটেজীগুলো জমা দিয়েছিলেন!

কিন্তু আরো একবার এই সব ন্যাস্টিনেস বা স্বার্থপরতা সুফল আনেনি। আবারো, টিট ফর ট্যাট, যা জমা দিয়েছিলেন আনাতোল রাসোপোর্ট বিজয়ী হয়েছিল এবং এটি বেঞ্চমার্ক স্কোরের বিশাল অংশশতকরা ৯৬ ভাগ পয়েন্ট অর্জন করেছিল। এবং আবারো নাইস স্ট্রাটেজীগুলো, খারাপ কৌশলগুলোর থেকে গড়পড়তায় ভালো করেছিল। সর্বোচ্চ স্কোর করা ১৫ টি কৌশলের মধ্যে মাত্র একটি ছাড়া সবগুলো ছিল নাইস’ এবং সর্বনিম্ন স্কোর করা ১৫টি কৌশলের মধ্যে একটি ছাড়া বাকী সবগুলোই খারাপ। কিন্তু যদিও সাধুসুলভ ‘টিট ফর টু ট্যাট’ প্রথম প্রতিযোগিতায় অংশ নিলে যা জয়ী হতে পারতো, সেটি দ্বিতীয় প্রতিযোগিতায় জেতেনি। এর কারণ ছিল খেলার ক্ষেত্রে আরো অনেক সূক্ষ্ম খারাপ কৌশল ছিল যা নিষ্ঠুরভাবে এ-ধরনের পুরোপুরি নীরিহ স্ট্রাটেজীর উপর আক্রমণ করতে পেরেছিল।

এটি এইসব প্রতিযোগিতায় একটি গুরুত্বপূর্ণ প্রসঙ্গ ইঙ্গিত করে। কোনো একটি কৌশলের সফলতা সেই প্রতিযোগিতায় ঘটনাচক্রে অংশ নেয়া অন্যান্য কৌশলের উপর নির্ভর করে। দুটি প্রতিযোগিতায়, দ্বিতীয়টিতে ‘টিট ফর টু ট্যাট’- এর তালিকায় নীচে নেমে আসা আর প্রথমটিতে যেখানে ‘টিট ফর টু ট্যাট’ বিজয়ী হতো এই পার্থক্যটিকে ব্যাখ্যা করার একটি মাত্র উপায় হচ্ছে এটি। কিন্তু এর আগে আমি যেমন বলেছি, এটি কম্পিউটার প্রোগ্রামারদের। উদ্ভাবনপটুতা ব্যাখ্যা করার কোনো বই নয়। আসলেই কি নৈর্ব্যক্তিক কোনো উপায় আছে যেখানে আমরা বিচার করতে পারি, কোনটা সেরা কৌশল, আরো সাধারণ আর অপেক্ষাকৃত কম মনগড়া কোনো উপায়ে? আগের অধ্যায়ের পাঠকরা ইতিমধ্যেই বিবর্তনীয়ভাবে স্থিতিশীল কৌশলের তত্ত্বে এর উত্তর অনুসন্ধান করার জন্য প্রস্তুত।

অ্যাক্সেলরড তার প্রতিযোগিতাটির প্রাথমিক ফলাফল যাদের মধ্যে প্রথম প্রচার করেছিলেন, আমি ছিলাম তাদের মধ্যে একজন, এবং সেখানে তিনি দ্বিতীয় প্রতিযোগিতায় কৌশল জমা দেবার জন্য আমন্ত্রণ জানিয়েছিলেন। আমি তা করিনি কিন্তু আমি আরেকটি প্রস্তাব দিয়েছিলাম। অ্যাক্সেলরড ইতিমধ্যে ‘ইএসএস’ অর্থেই পুরো ব্যাপারটা দেখতে শুরু করেছিলেন; কিন্তু আমি অনুভব করেছিলাম এই প্রবণতা এত বেশী গুরুত্বপূর্ণ যে আমি তাকে লিখেছিলাম, তার উচিৎ হবে ডাবলিউ, ডি, হ্যামিলটনের সাথে দেখা করা। যিনি ইতিমধ্যেই, যদিও অ্যাক্সেলরডের জানা ছিলনা, একই বিশ্ববিদ্যালয়ের অন্য একটি বিভাগে অবস্থান করছিলেন– ইউনিভার্সিটি অব মিশিগান। তিনি আসলেই সাথে সাথে হ্যামিলটনের সাথে যোগাযোগ করেছিলেন, এবং তাদের সেই সাক্ষাৎকারের ফলাফল হচ্ছে যুগভাবে লেখা একটি বৈজ্ঞানিক নিবন্ধ, যা প্রকাশিত হয়েছিল ১৯৮১ সালে সায়েন্স জার্নালে, যে পেপারটি আমেরিকান অ্যাসোসিয়েশন ফর দি অ্যাডভান্সমেন্ট অফ সায়েন্স এর নিউকম্ব ক্লিভল্যান্ড পুরষ্কার জিতেছিল। পুনরাবৃত্তি’ হওয়া প্রিজনার’স ডাইলেমার অদ্ভুত কিছু চমৎকার জৈববৈজ্ঞানিক উদাহরণ ব্যবহার করে, আমি মনে করি, অ্যাক্সেলরড এবং হ্যামিলটন ‘ইএসএস’ দৃষ্টিভঙ্গিকে তার প্রাপ্য স্বীকৃতি প্রদান করেছিলেন।

 ‘ইএসএস’ দৃষ্টিভঙ্গিটির সাথে অ্যাক্সেলরডের দুটি প্রতিযোগিতায় ব্যবহৃত ফুটবল লীগের মত ‘রাউন্ড রবিন পদ্ধতির পার্থক্যটি বোঝার চেষ্টা করুন। প্রতিটি কৌশল অন্য প্রতিটি কৌশলের সাথে খেলেছে সমান সংখ্যকবার। কোনো একটি কৌশলের চূড়ান্ত স্কোর হচ্ছে অন্য সব কৌশলের সাথে খেলায় প্রাপ্ত পয়েন্টের যোগফল। কোনো একটি রাউন্ড রবিন প্রতিযোগিতায় ভালো করতে হলে, সেই কৌশলকে অন্য সব কৌশল, যাদের প্রতিযোগিতায় অংশগ্রহন করার জন্য ঘটনাক্রমে জমা দেয়া হয়েছে, তাদের সবার সাথে ভালো করতে হবে। কোনো একটি কৌশল যা বেশ অনেকগুলো নানা ধরণের কৌশলের বিরুদ্ধে ভালো করে অ্যাক্সেলরড় তার নাম দিয়েছেন, ‘রোবাস্ট’ বা শক্তিশালী। টিট ফর ট্যাট’ কৌশলটি অবশেষে প্রমাণিত হলো একটি ‘রোবাস্ট’ কৌশল হিসাবে। কিন্তু যে সব কৌশল প্রতিযোগিতায় জমা দেয়া হয়েছিল সেগুলো মনগড়া। এই বিষয়টি উপরের আলোচনায় যা আমাদের সবচেয়ে চিন্তার বিষয়। ঘটনাচক্রেই কেবল মাত্র অ্যাক্সেলরডের মূল প্রতিযোগিতার অর্ধেক কৌশল ছিল ‘নাইস’। টিট ফর ট্যাট’ সেই পরিবেশে ভালো করেছে, এবং ‘টিট ফর টু ট্যাট’ সেই পরিবেশে জয়ী হতো যদি সেটি অংশ নিতো। কিন্তু মনে করুন যে প্রায় সব কৌশলগুলো যদি হতো ‘ন্যাস্টি’ বা খারাপ, খুব সহজেই কিন্তু সেটি হতে পারতো। কারণ ১৪ টি কৌশলের মধ্যে ৬ টি ছিল ‘ন্যাস্টি’। যদি ১৩টি কৌশল ন্যাস্টি হতো, টিট ফর ট্যাট’ জিততে পারতো না। কারণ সেই পরিবেশটি তার জন্য সঠিক হতো না। শুধুমাত্র টাকা জেতার পরিমান নয়, নানা কৌশলের সফলতার ক্রমতালিকা নির্ভর করে কোন কৌশলগুলো প্রতিযোগিতায় অংশ নিয়েছে। অন্যভাবে বললে এটি নির্ভর করে মানুষের ইচ্ছার মত মনগড়া এমন কিছুর উপর। কীভাবে আমরা এই মড়গড়া পরিস্থিতিটি হ্রাস করতে পারি? ‘ইএসএস’এর কথা চিন্তা করে।

 ‘ইএসএস’ বা বিবর্তনীয়ভাবে স্থিতিশীল কৌশলের একটি গুরুত্বপূর্ণ বৈশিষ্ট্য হচ্ছে, আগের অধ্যায়গুলো থেকে হয়তো আপনি মনে করতে পারবেন, এটি তার ভালো করা অব্যাহত রাখে যখন কোনো একটি কৌশল সমষ্টিতে এটি সংখ্যাগরিষ্ঠতা লাভ করে। “টিট ফর ট্যাট’ কৌশলটিকে একটি “ইএসএস’ বলা মানে, এমন কিছু বলা যে ‘টিট ফর ট্যাট’ ভালো করে এমন কোনো পরিস্থিতি ও পরিবেশে যেখানে ‘টিট ফর ট্যাট’ কৌশলটি প্রাধান্য বিস্তার করে। এটিকে দেখা যেতে পারে একটি বিশেষ ধরনের ‘রোবাস্টনেস’ বা শক্তিশালী হিসাবে। বিবর্তনবাদী হিসাবে আমরা প্ররোচিত হই এটিকে সবচেয়ে গুরুত্বপূর্ণ ধরনের ‘রোবাস্টনেস’ হিসাবে ভাবতে। কেনই বা এটি এত বেশী গুরুত্বপূর্ণ? কারণ, ডারউইনবাদের বিশ্বে, জয় লাভ করার পুরস্কার আমরা টাকার মাধ্যমে পাইনা, সন্তান দ্বারা তা পরিশোধিত হয়। কোনো একজন ডারউইনবাদীর কাছে, একটি সফল কৌশল হচ্ছে সেটি যে-কোনো কৌশল সমষ্টিতে সংখ্যাধিক্য লাভ করে। কোনো একটি কৌশলকে সফলতা ধরে রাখতে হলে, অবশ্যই একে ভালো করতে হবে যখন এদের সংখ্যা অনেক, সেটি হচ্ছে এমন একটি পরিবেশে যেখানে প্রাধান্য বিস্তার করে এর নিজেরই অনুলিপিগুলো।

 অ্যাক্সেলরড, বাস্তবিকভাবে, তার প্রতিযোগিতার তৃতীয় রাউন্ডটি পরিচালনা করেছিলেন এমনভাবে যেভাবে প্রাকৃতিক নির্বাচন হয়তো এটি পরিচালনা করতো, একটি ‘ইএসএস’ অনুসন্ধান করার মাধ্যমে। আসলে তিনি এটিকে তৃতীয় রাউন্ড বলতেও চাননি কারণ তিনি কোনো নতুন স্ট্রাটেজী আহবান করেননি বরং সেই একই ৬৩টি স্ট্রাটেজী ব্যবহার করেছিলেন যা তিনি দ্বিতীয় রাউন্ডে ব্যবহার করেছিলেন। আমার জন্য সুবিধাজনক এটিকে তৃতীয় রাউন্ড হিসাবে ভাবা। কারণ আমি মনে করি এটি আগের দুটি রাউন্ড রবিন প্রতিযোগিতা থেকে অনেক বেশী মৌলিকভাবে আলাদা, দুটি রাউন্ড রবিন প্রতিযোগিতা পরস্পর থেকে যতটা ভিন্ন তার চেয়েও বেশী।

অ্যাক্সেলরড ৬৩টি কৌশল কম্পিউটারে পরস্পরের সাথে প্রতিযোগিতা করার সুযোগ দেন একটি বিবর্তনীয় ধারাবাহিকতায় ‘প্রজন্ম ১’ সৃষ্টি করার জন্য। সুতরাং প্রজন্ম ১ এর ‘পরিবেশে’ ৬৩ কৌশলের প্রত্যেকটির সমান প্রতিনিধিত্ব আছে। প্রজন্ম ১ এর শেষে, প্রতিটি কৌশলের অর্জিত পয়েন্ট পরিশোধ করা হয় অর্থ বা পয়েন্ট হিসাবে নয় বরং ‘সন্তান’ হিসাবে, যারা তাদের (অযৌন) পিতামাতার হুবহু। প্রজন্মান্তরে, কিছু কৌশল ক্রমশ সংখ্যায় কমে যায় এবং দুষ্প্রাপ্য থেকে ক্রমশ বিলুপ্ত হয়। অন্য কৌশলগুলো ক্রমশ সংখ্যায় বৃদ্ধি পেতে থাকে। এবং যখন আনুপাতিক অংশের হার বদলাতে থাকে, পরিণতি হিসাবে সেই পরিবেশও বদলাতে থাকে যেখানে খেলার ভবিষ্যৎ দানগুলো চলতে থাকে।

এভাবে অবশেষে প্রায় ১০০০ প্রজন্মের পর, আনুপাতিক হারের আর কোনো পরিবর্তন ঘটে না। স্থিতিশীলতা অর্জিত হয়। তবে এর আগে নানা কৌশলের ভাগ্য কখনো প্রসন্ন এবং কখনো অপ্রসন্ন হয়, ঠিক যেমন ঘটে আমার ‘চিট’, ‘সাকার’ এবং গ্রাজারদের কম্পিউটার সিমুলেশনে। কিছু কৌশল শুরু থেকে বিলুপ্ত হতে শুরু করে এবং বেশীর ভাগই বিলুপ্ত হয় প্রজন্ম সংখ্যা ২০০ এ। ন্যাস্টি বা খারাপ কৌশলগুলোর মধ্যে একটি বা দুটি বাড়তে থাকে সংখ্যায়, কিন্তু তাদের সফলতা আমার সিমুলেশনে চিটদের মত ক্ষণস্থায়ী। যে একটি মাত্র ন্যাস্টি বা খারাপ কৌশল প্রজন্ম ২০০ র পরে টিকে থাকে তার নাম ‘হ্যারিংটন। হ্যাঁরিংটনের ভাগ্য দ্রুত প্রসন্ন হতে হতে থাকে প্রথম ১৫০ প্রজন্মে, এরপর এটি ধীরে ধীরে কমতে থাকে এবং বিলুপ্তির মুখোমুখি হয় প্রজন্ম ১০০০ এর কাছাকাছি। আমার সিমুলেশনের সেই মূল ‘চিট’ যেমন করেছিল, ‘হ্যারিংটন’ সাময়িকভাবে একই কারণে ভালো করেছিল। এটি মৃদুপন্থী যেমন, ‘টিট ফর টু ট্যাট’দের তার নিজের স্বার্থে ব্যবহার করে, যখন এই কৌশলগুলোর অস্তিত্ব থাকে। এরপর এই সব মৃদুপন্থীরা যখন বিলুপ্ত হতে শুরু করে হ্যাঁরিংটন কৌশলটিরও একই পরিণতি অনুসরণ করতে হয়, কারণ ব্যবহার করার মত তাদের আর কোনো শিকার থাকেনা। পুরো ক্ষেত্র থাকে মুক্ত ‘নাইস’ কিন্তু প্রয়োজনে খারাপ হতে পারে এমন কৌশল যেমন, টিট ফর ট্যাট এর জন্য।

‘টিট ফর ট্যাট’ নিজে, আসলেই রাউন্ড তিনের ছয়টি পর্যায়ের পাঁচটিতেই শীর্ষ স্থান দখল করে, যেমন এটি করেছিল রাউন্ড ১ ও ২ তে। নাইস কিন্তু প্রয়োজনে খারাপ হতে পারে এমন আর পাঁচটি কৌশলও প্রায় একই করম সফল হয় (জনসংখ্যায় তাদের উপস্থিতির হার বাড়ে) যেমন, টিট ফর ট্যাট; আসলেই, তাদের একটি ষষ্ঠ রাউন্ডে জয় লাভও করে। যখন সব ‘ন্যাস্টি’ কৌশল বিলুপ্ত হয়, সেখানে আর কোনো উপায় থাকেনা একটি নাইস কৌশলকে টিট ফর ট্যাট থেকে আলাদা বা একটিকে অপরের সাথে পৃথক করা যায়, কারণ তারা সবাই, ‘নাইস’ হবার কারণে, সাধারণভাবে একে অপরের সাথে সহযোগিতার কার্ড খেলে যায়।

এই অবিভেদ্যতার একটি পরিণতি হচ্ছে, যদিও ‘টিট ফর ট্যাট’কে একটি ‘ইএসএস’-এর মত মনে হয়, এটি কঠোরভাবে সত্যিকারের ‘ইএসএস’ নয়। একটি ‘ইএসএস’ হতে হলে, মনে রাখতে হবে যে, একটি স্ট্রাটেজী অবশ্যই কোনো দূর্লভ, পরিবর্তিত কৌশলের দ্বারা অনাক্রম্য হতে হবে, যখন এটি সংখ্যায় বেশী থাকবে। যদিও এটি সত্যি যে ‘টিট ফর ট্যাট’ কৌশলের মধ্যে ন্যাস্টি কোনো কৌশল আগ্রাসন করতে পারবেনা, কিন্তু অন্য কোনো নাইস কৌশলের জন্য অবশ্য ভিন্ন কথা। যেমন, আমরা এই মাত্র দেখলাম, ‘নাইস’ কৌশলগুলো কোনো জনসংখ্যায় দেখতে ও আচরণে পরস্পর সদৃশ্য হবে: তারা সব সময়ই একে অপরের সহযোগিতা করবে। সুতরাং যে-কোনো নাইস কৌশল, যেমন পুরোপুরি সাধুসুলভ কৌশলের মতই সবসময় সহযোগিতা করে, যদিও স্বীকার করতে হবে, এটি কোনো ইতিবাচক নির্বাচনী সুবিধা পায়না ‘টিট ফর ট্যাট’-এর চেয়ে বেশী, কিন্তু তারপরও জনগোষ্ঠীতে কোনো দৃষ্টি আকর্ষণ না করে এটি ছড়িয়ে পড়তে পারে। সুতরাং টেকনিকালী টিট ফর ট্যাট ‘ইএসএস’ নয়।

আপনি হয়তো ভাবতে পারেন যেহেতু পৃথিবী একই রকম নাইস থাকে, আমরা ‘টিট ফর ট্যাটকে একটি ‘ইএসএস’ হিসাবে গন্য করতে পারি। কিন্তু হায়, এর পরে কি হয় দেখুন, টিট ফর ট্যাট এর ব্যতিক্রম, সবসময় সহযোগিতা কিন্তু আগ্রাসন থেকে সুরক্ষিত বা স্থিতিশীল নয়, যখন কোনো ন্যাস্টি কৌশল যেমন ‘সবসময় অসহযোগিতা বা বিশ্বাসঘাতকতা সেখানে অনুপ্রবেশ করে। সবসময় বিশ্বাসঘাতকতা, সবসময় সহযোগিতা স্ট্রাটেজীর বীপরিতে বেশ ভালো করে সবসময়ই, কারণ এটি প্রতিবারই প্রলোভনের উচ্চ পয়েন্ট পায়। সবসময় বিশ্বাসঘাতকতার মত ‘ন্যাস্টি’ কোনো কৌশল সব সময়ই অনুপ্রবেশ করে বেশী নাইস কৌশলগুলোর সংখ্যা দমিয়ে রাখার জন্য যেমন ‘সবসময় সহযোগিতা।

কিন্তু যদিও ‘টিট ফর ট্যাট’ খুব কঠোরভাবে বললে একটি সত্যিকারের ‘ইএসএস’ না, সম্ভবত সুবিচার হবে মৌলিকভাবে ‘নাইস’ কিন্তু বদলা নিতে পারা’ ‘টিট ফর ট্যাট’ সদশ কৌশলগুলোর কোনো একধরণের মিশ্রণকে প্রায়োগিক ক্ষেত্রে মোটামুটিভাবে একটি ‘ইএসএস’ সমতুল্য হিসাবে বিচার করতে। এধরণের মিশ্রণে হয়তো সামান্য কিছু ‘ন্যাস্টিনেস’ মিশ্রিত থাকবে। রবার্ট বয়েড এবং জেফরী লোরবেরবাম, অ্যাক্সেলরডের গবেষণার একটি কৌতূহলোদ্দীপক সমরুপ গবেষণায় ‘টিট ফর টু ট্যাট’ এবং একটি স্ট্রাটেজী যার নাম দেয়া হয়েছে “সন্দেহজনক টিট ফর ট্যাট’ স্ট্রাটেজী, দুটির মিশ্র একটি স্ট্রাটেজী নিয়ে গবেষণা করেছিলেন। “সন্দেহজনক টিট ফর ট্যাট’ স্ট্রাটেজী কারিগরীভাবে খারাপ বা ন্যাস্টি স্ট্রাটেজী তবে খুব বেশী খারাপ নয়। এটি ঠিক নিজে টিট ফর ট্যাট এর মত আচরণ করে প্রথম দানের পরে, কিন্তু– যা এটিকে কারিগরীভাবে খারাপ বা ন্যাস্টি স্ট্রাটেজী হিসাবে চিহ্নিত করে সেটি হচ্ছে– খেলার প্রথম দানেই এটির অসহযোগিতা বা বিশ্বাসঘাতকতা করা। এমন কোনো পরিবেশে যেখানে পুরোপুরিভাবে প্রাধান্য বিস্তার করে টিট ফর ট্যাট, “সন্দেহজনক টিট ফর ট্যাট’ স্ট্রাটেজী খুব একটা সুবিধা করতে পারেনা, কারণ এর শুরু বিশ্বাসঘাতকতা পারস্পরিক বদলা নেবার একটি অবিচ্ছিন্ন চক্রের সূচনা করে। যখন এটি একটি ‘টিট ফর টু ট্যাট’ খেলোয়াড়ের মুখোমুখি হয়, অন্যদিকে, ‘টিট ফর টু ট্যাট’ এর বাড়তি ক্ষমাশীলতা এই প্রতিহিংসা চক্রকে অঙ্কুরে বিনষ্ট করে। উভয় খেলোয়াড়ই খেলা শেষ করে কমপক্ষে বেঞ্চমার্ক সমান পয়েন্ট অর্জন করে, এবং “সন্দেহজনক টিট ফর ট্যাট স্ট্রাটেজী’ এর প্রাথমিক বিশ্বাসঘাতকতার জন্য একটি বোনাস পয়েন্ট অর্জন করে। বয়েড এবং লোরবেরবম দেখান যে-কোনো একটি ‘টিট ফর ট্যাট’ স্ট্রাটেজীর জনগোষ্ঠী আগ্রাসনের শিকার হতে পারে, বিবর্তনীয়ভাবে বলা যায়, টিট ফর টু ট্যাট ও এবং সন্দেহজনক টিট ফর ট্যাট স্ট্রাটেজীর একটি মিশ্রণ দ্বারা, এবং দুটোই একে অপরের সাহচর্যে বেশ ভালো করে। এবং এই সংমিশ্রণ অবশ্যই শুধুমাত্র একটি কম্বিনেশন নয় যা এভাবে আগ্রাসন করতে পারে। সম্ভবত আরো অনেক এধরণের মিশ্র স্ট্রাটেজী আছে কিছুটা ন্যাস্টি স্ট্র্যাটেজি এবং খুব বেশী ক্ষমাসূলভ স্ট্র্যাটেজীর মিশ্রণ যারা যৌথভাবে আগ্রাসন করতে সক্ষম। কেউ হয়তো এটিকে দেখতে পারেন মানব জীবনের সমরুপ বিষয়গুলোর প্রতিফলন হিসাবে।

অ্যাক্সেলরড শনাক্ত করেছিলেন যে, টিট পর ট্যাট খুব কঠোরভাবে ভাবলে একটি ‘ইএসএস’ নয়, এবং সে কারণে তিনি সেই ‘কালেকটিভলী স্টেবল স্ট্রাটেজী’ বা ‘সম্মিলিতভাবে স্থিতিশীল কৌশল’ বাক্যটির উদ্ভাবন করেছিলেন বিষয়টি ব্যাখ্যা করার জন্য। সত্যিকারের কোনো ইএসএস’ এর মত, এটাও সম্ভব যে একাধিক কৌশল একই সাথেসম্মিলিতভাবে স্থিতিশীল হতে পারে। এবং আবারো, ভাগ্যের ব্যাপার কোনটি জনগোষ্ঠীতে প্রাধান্য বিস্তার করবে। সবসময় বিশ্বাসঘাতকতাও স্থিতিশীল, টিট ফর ট্যাটও তাই। কোনো একটি জনগোষ্ঠী যেখানে ইতিমধ্যেই প্রাধান্য বিস্তার করেছে ‘সবসময় বিশ্বাসঘাতকতা’, সেখানে আর কোনো কৌশলই ভালো করতে পারেনা। আমরা পুরো সিস্টেমটাকে দুটি বিন্দুতে স্থিতিশীল হিসাবে ভাবতে পারি, যেখানে সবসময় বিশ্বাসঘাতকতা স্থিতিশীল বিন্দুর একটি। টিট ফর ট্যাট (অথবা সবসময় নাইস, প্রয়োজনে বদলা নেয় এমন কৌশলের কোনো মিশ্রণ) অথবা অন্য কোনো স্থিতিশীল পয়েন্ট। যে স্থিতিশীল পয়েন্টটি জনগোষ্ঠীতে প্রাধান্য বিস্তার করে প্রথম, সেটি সাধারণত তার প্রাধান্য বজায় রাখে।

কিন্তু পরিমাপবাচক অর্থে এই প্রাধান্য বিস্তার’ বলতে আসলে কি বোঝাচ্ছে? কত সংখ্যক টিট ফর ট্যাটকে অবশ্যই সেখানে থাকতে হবে ‘সবসময় বিশ্বাসঘাতক’ থেকে টিট ফর ট্যাট এর ভালো করার জন্য। সেটি নির্ভর করবে বিস্তারিত মূল্য পরিশোধের উপর যা ব্যাঙ্কার রাজী হয় সেই খেলার সময় বিতরণ করার জন্য। আমরা যা বলতে পারি সাধারণভাবে সেটি হচ্ছে সেখানে একটি ক্রিটিকাল হার থাকে, একটি নাইফ-এজ বা ছুরির ধার। যে ছুরির এক ধারে টিট ফর ট্যাট তার প্রয়োজনীয় হার অতিক্রম করেছে এবং নির্বাচন আরো বেশী টিট ফর ট্যাট এর পক্ষে। ছুরির ধারের অন্যদিকে সবসময় বিশ্বাসঘাতকতার গুরুত্বপূর্ণ হারটি অতিক্রম করে এবং নির্বাচন আরো বেশী সবসময় বিশ্বাসঘাতকতাকে সমর্থন করে। এই ছুরির ফলার সমরুপ একটি বিষয়ের সাথে আগে পরিচিত হয়েছি আমরা, আপনি হয়তো মনে করতে পারবেন, অধ্যায় ১০ এ গ্রাজার এবং চিটদের গল্প বলার সময়।

সেকারণে এটি অবশ্যই গুরুত্বপূর্ণ, ছুরির ধারের যেকোনো একটি পাশ থেকে জনগোষ্ঠী ঘটনাচক্রে তাদের যাত্রা শুরু করে। এবং আমাদের জানা দরকার কি ঘটে যে একটি জনগোষ্ঠী কখনো কখনো চুরির ফলার এক ধার থেকে অন্য ধার অতিক্রম করে। মনে করুন আমরা একটি জনগোষ্ঠী নিয়ে শুরু করলাম যা ইতিমধ্যেই বসে আছে। ‘সবসময় বিশ্বাসঘাতকতার দিকে। অল্প কিছু টিট ফর ট্যাট’ সদস্যরা তাদের পারস্পরিক উপকারের জন্য একে অপরের সাথে যথেষ্ট সংখ্যকবার মিলিত হতে পারেনা। সুতরাং প্রাকৃতিক নির্বাচন জনগোষ্ঠীকে আরো বেশী সবসময় বিশ্বাসঘাতকতার চরম প্রান্তের দিকে ঠেলে নিয়ে যায়। যদি শুধুমাত্র জনগোষ্ঠী কোনো না কোনোভাবে মানিয়ে নিতে পারে, র‍্যানডোম ভাবে সরে গিয়ে, তার নিজেকে ছুরির ধারের অন্য প্রান্তের দিকে সরিয়ে নিয়ে, এটি তাহলে টিট ফর ট্যাট ধার বেয়ে সহজে নিম্নমুখী হবে এবং সবাই বেশ ভালো করবে ব্যাঙ্কারের (অথবা প্রকৃতির) ক্ষতির বিনিময়ে। কিন্তু অবশ্যই জনগোষ্ঠীর কোনো গোষ্ঠীগত ইচ্ছা নেই, উদ্দেশ্য নেই। তারা সচেতনভাবে ছুরির ধার লাফ দেবার জন্য কোনো সংগ্রাম করেনা। তারা সেটি অতিক্রম করে শুধুমাত্র যদি প্রকৃতির নির্দেশনাহীন শক্তি তাদের সেদিকে ঘটনাচক্রে তাড়িত করে।

কিন্তু কীভাবে এটি ঘটতে পারে? একটি উপায়ে এই প্রশ্নের উত্তরটি প্রকাশ করা যেতে পারে, সেটি হচ্ছে এটি হয়তো ঘটতে পারে চান্স বা আপতনের মাধ্যমে। কিন্তু চান্স’ হচ্ছে এমন একটি শব্দ যা কোনো বিষয় সম্বন্ধে আমাদের অজ্ঞতাকে প্রকাশ করে। এর অর্থ হচ্ছে ‘এটি নির্ধারিত হয় এমন কিছু দ্বারা যা এখনো অজানা অথবা সুনির্দিষ্ট নয়, এমন উপায়ে’; আমরা ‘চান্স’ এর আরো একটু বেশী ভালো করতে পারি। আমরা ব্যবহারিক কোনো উপায়ের কথা ভাবার চেষ্টা করতে পারি যেখানে সংখ্যালঘু ‘টিট ফর ট্যাট’ কৌশলীরা হয়তো সংখ্যায় বৃদ্ধি পেয়ে ‘ক্রিটিকাল মাস’ তৈরী করতে পারে। এটি সমতুল্য সেই সব সম্ভাব্য সব উপায়ের অনুসন্ধান করা যেখানে টিট ফর ট্যাট কৌশলীরা এক সাথে জড়ো হয় যথেষ্ট পরিমান সংখ্যায় যে তারা প্রত্যেকেই লাভবান হয় ব্যাঙ্কারের ক্ষতি করে।

এভাবে চিন্তার করাটা বেশ প্রতিশ্রুতিশীল মনে হয়, কিন্তু এটি বরং বেশ অস্পষ্ট। ঠিক কিভাবে পরস্পর সদৃশ একক সদস্যরা নিজেদের একটি জায়গায় সমবেত হয়েছে দেখতে পারে, কোনো স্থানীয়ভাবে সম্মিলন হিসাবে? প্রকৃতিতে, সবচেয়ে সুস্পষ্ট উপায় হচ্ছে জিনগত সম্পর্কর মাধ্যমে, কিনশিপ বা আত্মীয়তা। বেশীর ভাগ প্রজাতির প্রাণীদের সাধারণত তাদের বোন, ভাই এবং জ্ঞাতিভাইদের নিকটেই বসবাস করার সম্ভাবনা থাকে জনগোষ্ঠীতে অন্য যে কোনো সদস্যদের নিকটে বসবাস করার তুলনায়। এটি আবশ্যিকভাবে তাদের পছন্দের উপর নির্ভরশীল না। এটি স্বয়ংক্রিয়ভাবে ঘটে জনগোষ্ঠীর ‘ভিসকোসিটির বা সান্দ্রতার উপর। এখানে ‘সান্দ্রতার অর্থ হচ্ছে প্রজাতির কোনো একক সদস্যদের যেখানে জন্ম হয়েছে। সেই এলাকার কাছাকাছি বসবাস করার প্রবণতা। যেমন, ইতিহাসের বেশীর ভাগ সময় জুড়ে এবং পৃথিবীর বেশীর ভাগ জায়গায় (যদিও, দেখা যাচ্ছে আধুনিক যুগে নয়) একক কোনো মানব সদস্য কদাচিৎ তার জন্মস্থান থেকে কয়েক মাইল দুরে যেত। ফলাফলে, স্থানীয়ভাবে জিনগত আত্মীয়দের গ্রুপ গড়ে ওঠার প্রবণতা ছিল। আমি মনে করতে পারছি একটি দুর্গম দ্বীপে ভ্রমনের কথা, দ্বীপটি আয়ারল্যান্ডের পশ্চিম উপকুলে, সেখানে বেশ চোখে পড়ার মত একটি পর্যবেক্ষণ ছিল যে, দ্বীপের প্রায় সবারই বিশালাকার জগের হাতলের মত কান ছিল। স্থানীয় জলবায়ুর জন্য এটি মানানসই এমন কোনো কারণ হবার সম্ভাবনা খুব ক্ষীণ (কারণ সেখানে সমুদ্র থেকে আসা বাতাসের তীব্রতাও খুব বেশী); এর কারণ এই দ্বীপের বেশীর ভাগ অধিবাসীরা একে অপরের নিকটাত্মীয়।

জিনগত আত্মীয়দের পরস্পর সদৃশ হবার প্রবণতা আছে শুধু মুখের বিশেষ বৈশিষ্ট্যতেই নয় অন্য আরো অনেক ক্ষেত্রেও। যেমন, তাদের পরস্পর সদৃশ হয় জিনগতভাবে টিট ফর ট্যাট খেলার– অথবা না খেলার– প্রবণতায়। সুতরাং এমনকি যদিও ‘টিট ফর ট্যাট’ দুর্লভ সার্বিকভাবে কোনো জনগোষ্ঠীতে, তবে তারা স্থানীয়ভাবে বেশী দুর্লভ নাও হতে পারে। কোনো একটি স্থানীয় এলাকায়, টিট ফর ট্যাট একক সদস্যরা প্রায়শই পরস্পরের সাথে যথেষ্ট পরিমান বেশী ক্রিয়া-প্রতিক্রিয়া করার সম্ভাবনা থাকে যে পারস্পরিক সহযোগিতা থেকে তারা উপকার পেতে পারে, এমনকি যদিও কোনো গণনায় যা জনগোষ্ঠীর সেই সামগ্রিক হারটির কথা বিবেচনা করেন, সেটি হয়তো ইঙ্গিত করতে পারে যে তাদের পরিমান ছুরির প্রান্তের ক্রিটিকাল হারের নীচেই অবস্থান করছে।

যদি এটি ঘটে থাকে, টিট ফর ট্যাট সদস্যরা, একে অপরের সাথে সহযোগিতা করে তাদের নিজস্ব ছোট স্থানীয় এলাকায়, তারা এতটাই ভালো করে যে, তারা স্থানীয় কোনো গ্রুপ থেকে আকারে বড় হয়ে আরো বড় স্থানীয় গ্রুপ তৈরী করে। এই সব স্থানীয় গ্রুপগুলো আকারে এত বেশী বড় হয় যে তারা অন্যান্য এলাকাতেও ছড়িয়ে পড়ে, এমনকি সেই সব এলাকাতেও যেখানে এ যাবৎ প্রাধান্য বিস্তার করেছে, সংখ্যাগতভাবে সেই সব সদস্যদের দ্বারা যারা ‘সবসময় বিশ্বাসঘাতকতা করে। এই সব স্থানীয় এলাকাগুলো, আমার আইরিশ দ্বীপ একটি বিভ্রান্তি সৃষ্টিকারী উদাহরণ কারণ এটি ভৌগলিকভাবেই বিচ্ছিন্ন। বরং এর পরিবর্তে চিন্তা করুন কোনো একটি বিশাল জনগোষ্ঠীর কথা যেখানে তেমন বেশী কোনো অবস্থান পরিবর্তন নেই, সুতরাং একক সদস্যরা তাদের নিকটের প্রতিবেশীদের সদৃশ হয় অনেক বেশী তাদের দুরবর্তী প্রতিবেশীদের তুলনায়, এমনকি যদিও সেখানে নিরন্তরভাবে আন্তঃপ্রজনন চলে পুরো এলাকা জুড়ে।

আবারো আমরা সেই ছুরির-ফলার উদাহরণে আসি, এরপর তাহলে টিট ফর ট্যাট সেই সীমা অতিক্রম করতে পারবে। যা প্রয়োজন তা হলো খানিকটা স্থানীয়ভাবে একটি গ্রুপ সৃষ্টি, এমন কোনো কিছু যা খুব স্বাভাবিকভাবে প্রাকৃতিক কোনো জনগোষ্ঠীতে উদ্ভব হতে পারে। টিট ফর ট্যাট এর একটি অন্তর্গত বৈশিষ্ট্য আছে– এমনকি যখন এটি দূর্লভ– ছুরির সীমা পেরিয়ে এর নিজের দিকে প্রত্যাবর্তন করার। যেন মনে হবে এই ছুরি প্রান্তের নীচের দিকে কোনো গোপন পথ আছে। কিন্তু সেই গোপন পথটি নিয়ন্ত্রণ করছে শুধুমাত্র একদিকে যাতায়াত নিশ্চিৎ করে এমন কোনো কপাটিকা: এখানে একটি অপ্রতিসাম্যতা আছে। টিট ফর ট্যাট এর ব্যতিক্রম ‘সবসময় বিশ্বাসঘাতকতা’, যদিও সত্যি একটি ইএসএস, ছুরি ধার অতিক্রম করার জন্য তারা স্থানীয় গ্রুপ ব্যবহার করতে পারে না। বরং এর বিপরীত, স্থানীয় সবসময় বিশ্বাসঘাতক’ গ্রুপগুলোর সদস্যরা, একে অপরের উপস্থিতিতে লাভবান হবার বদলে বিশেষভাবে খারাপ করে একে অপরের সান্নিধ্যে। ব্যাঙ্কারের ক্ষতি করে পরস্পরকে নীরবে সাহায্য করার বদলে তারা পরস্পরের ক্ষতি করে। “সবসময় বিশ্বাসঘাতকতা’, সেকারণে ‘টিট ফর ট্যাট’ এর ব্যতিক্রম আত্মীয়তা অথবা জনগোষ্ঠীতে সান্দ্রতা থেকে কোনো উপকার পায়না।

সুতরাং যদিও ‘টিট ফর ট্যাট’ হতে পারে একমাত্র সন্দেহজন ‘ইএসএস’, এর একধরণের একটি উচ্চতর পর্যায়ের স্থিতিশীলতা আছে। এর কি মানে হতে পারে? নিশ্চয়ই যা স্থিতিশীল তার তো স্থিতিশীল হবার কথা। বেশ, এখানে আমরা একটি দীর্ঘতর দৃষ্টির সাহায্য নিচ্ছি। সবসময় বিশ্বাসঘাতক’ দীর্ঘসময় ধরে কোনো আগ্রাসনকে প্রতিহত করতে পারে। কিন্তু যদি আমরা যথেষ্ট পরিমান দীর্ঘ সময় অপেক্ষা করি, হয়তো বহু হাজার বছর, “টিট ফর ট্যাট’ ধীরে ধীরে সেই সংখ্যাধিক্য অর্জন করে যা ছুরির প্রান্তসীমা অতিক্রম করতে পারে। এবং পুরো জনগোষ্ঠী বদলে যায়। কিন্তু এর উল্টোটা কখনো হবে না। সবসময় বিশ্বাসঘাতকতা’, যেমনটি আমরা দেখেছি, একসাথে জমায়েত বাধা থেকে কোনো সুবিধা আদায় করতে পারেনা এবং সে কারণে উচ্চতর পর্যায়ের স্থিতিশীলতা অর্জন করতে পারেনা।

 টিট ফর ট্যাট, যেমনটি আমরা দেখেছি, একটি ভালো বা নাইস’ স্ট্রাটেজী, যার অর্থ প্রথমে কখনোই বিশ্বাসঘাতকতা না করা এবং ক্ষমাশীল কারণ অতীতের অপকর্ম বেশী দিন মনে রাখার মত তার দীর্ঘ মেয়াদী স্মৃতি নেই। আমি এখন অ্যাক্সেলরডের আরেকটি ইঙ্গিতবহ কারিগরী শব্দের সাথে পরিচিত হই। টিট ফর ট্যাট একই সাথে খুব বেশী ঈর্ষাকাতর নয়। ঈর্ষাকাতর হতে হলে, আক্সেলরডের ভাষায়, অন্যান্য খেলোয়াড়ের চেয়ে বেশী অর্থ উপার্জনের জন্য সংগ্রাম করতে হবে, ব্যাঙ্কারের টাকার পুরোপুরিভাবে বিশাল অংশ পাবার চেয়েও। ঈর্ষাকাতর না হওয়া মানে বেশী খুশী হওয়া যে অন্য খেলোয়াড়ও আপনার মতই সমপরিমান অর্থ জয় করে, যতক্ষণ না পর্যন্ত ব্যাঙ্কারের কাছ থেকে আপনারা দুজনেই আরো বেশী অর্থ উপার্জন করেন। টিট ফর ট্যাট কখনো আসলেই কোন খেলায় জয়লাভ করেনা। বিষয়টি নিয়ে ভাবুন এবং আপনি দেখতে পাবেন এটি এর প্রতিপক্ষ থেকে কখনোই বেশী বেশী পরিমান লাভ অর্জন করতে পারেনা কোনো একটি নির্দিষ্ট খেলায় কারণ এটি কখনোই বিশ্বাসঘাতকতা করেনা শুধুমাত্র বদলা নেয়ার সময় ছাড়া। বড় জোর এটি যা করতে পারে তা হলো এর প্রতিপক্ষের সাথে ড্র করে। কিন্তু এটি প্রতিবারই ড্র অর্জন করে,যখন দুজনেই লাভই এককরমভাবে অনেক বেশী হয়। যখন আমরা টিট ফর ট্যাট বা অন্যান্য নাইস স্ট্রাটেজী নিয়ে কথা বলি, ‘প্রতিপক্ষ’ শব্দটিই অপ্রযোজ্য এখানে। দুঃখজনকভাবে যদিও যখন মনোবিজ্ঞানীরা ‘পুনরাবৃত্তি হওয়া প্রিজনার’স ডাইলেমা গেমটি সাজান সত্যিকারের মানুষদের মধ্যে, প্রায় প্রতিটি খেলোয়াড়ই ঈর্ষার শিকার হন এবং সেকারণে অর্থ উপার্জনের বিবেচনায় তারা অপেক্ষাকৃতভাবে খারাপ ফলাফল করেন। মনে হতে পারে যে বহু মানুষ, হয়তো এমনকি কোনো কিছু চিন্তা না করে, অন্য খেলোয়াড়ের সাথে সহযোগিতা করে ব্যাঙ্কারের ক্ষতি করার বদলে বরং অন্য খেলোয়াড়ের সাথে বিশ্বাসঘাতকতা করার সিদ্ধান্ত নেয়। অ্যাক্সেলরডের কাজ প্রদর্শন করে কি বড় ধরনের ভুল ছিল এটি।

এটি শুধুমাত্র কিছু বিশেষ ধরনের খেলার জন্য ভুল। গেম তাত্ত্বিকরা খেলাগুলো বিভক্ত করেন দুটি প্রকারে– ‘জিরো সাম’ এবং ননজিরো সাম’। কোনো একটি ‘জিরো সাম’ গেম হচ্ছে সেই গেম যেখানে কোনো একক খেলোয়াড়ের জন্য বিজয় মানে অন্য জনের জন্য পরাজয়। দাবা হচ্ছে ‘জিরো সাম’, কারণ প্রতিটি খেলোয়াড়ের লক্ষ্য হচ্ছে জয় লাভ করা, এর মানে হলো অন্য খেলোয়াড়কে পরাজিত করা। প্রিজনার’স ডাইলেমা, তবে, একটি নন-জিরো সাম’ গেম। একজন ব্যাঙ্কার আছে যিনি টাকা দেন, এবং এটি সম্ভব দুজন খেলোয়াড় জোট বেধে হাসতে হাসতে ব্যাঙ্কে যেতে পারেন। এই হাসতে হাসতে ব্যাঙ্কে যাওয়ার কথাটি আমাকে শেকসপিয়ার এর একটি চমৎকার উক্তির কথা মনে করিয়ে দিলো:

 ‘প্রথম যে জিনিসটি আমরা করবো, আসুন সব উকিলদের হত্যা করি। হেনরী (চতুর্থ)

যাকে আমরা সাধারণ সামাজিক ‘দ্বন্দ্ব’ বলি, সেখানে প্রায়শই বাস্তবিকভাবে সহযোগিতার একটি বিশাল সুযোগ থাকে। যাকে দেখলে মনে হয় একটি জিরো সাম দ্বন্দ্ব, সেটি একটু সদিচ্ছা থাকলেই রূপান্তরিত হতে পারে পারস্পরিক সহযোগিতাপূর্ণ নন জিরো সাম গেমে। বিবাহ বিচ্ছেদের কথা ভাবুন, একটি ভালো বিয়ে অবশ্যই নন-জিরো সাম গেম, যা পারস্পরিক সহযোগিতাপূর্ণ। এবং এমনকি যখন এটি ভেঙ্গে পরে, সেখানে বহু ধরনের কারণ থাকে কেন সেই দম্পতির প্রত্যেকেই লাভবান হতে পারে সহযোগিতা অব্যাহত রেখে এবং তাদের বিবাহ বিচ্ছেদকেও একটি নন-জিরো সাম গেম হিসাবে বিবেচনা করে। সন্তানদের কল্যাণ যথেষ্ট গুরুত্বপূর্ণ কারণ হিসাবে তো আছেই, আইনজীবিদের পারিশ্রমিকও পারিবারিক খরচের উপর খারাপ প্রভাব ফেলবে, সুতরাং স্পষ্টতই কোনো কাণ্ডজ্ঞান সম্পন্ন দম্পতি একটি আইনজীবির কাছে যৌথভাবে যাবার মাধ্যমে শুরু করে। তাই না?

বেশ, আসলেই তা নয়। অন্তত ইংল্যান্ডে সাম্প্রতিক সময়ের আগে, যুক্তরাষ্ট্রের পঞ্চাশটি রাজ্যে, আইন বা আরো সুস্পষ্টভাবে বলতে গেলে এবং আরো বেশী গুরুত্বপর্ণভাবে– আইনজীবিদের পেশাগত বিধি অনুযায়ী, তাদের একই সাথে একই দম্পতির দুজনের আইনজীবি হতে অনুমতি দেয়না। কোনো দম্পতির যেকোনো একজনকে মাত্র তারা তাদের মক্কেল বানাতে পারেন। অন্যজনকে দরজা থেকেই ফিরিয়ে দেয়া হয় এবং হয় তার কোনো আইনগত উপদেশ নেই একদম অথবা তারা অন্য একজন আইনজীবির শরণাপন্ন হতে বাধ্য হন। এবং তখনই কেবল আসল মজা শুরু হয়। আলাদা আলাদা কক্ষে কিন্তু একটি কণ্ঠস্বরে, দুই আইনজীবি তাৎক্ষণিকভাবে ‘আমরা” এবং “ওরা” হিসাবে নিজেদের চিহ্নিত করতে শুরু করে। আমরা–আপনি বুঝতে পারছেন– এর মানে কিন্তু আমি এবং আমার স্ত্রী নয়: এর অর্থ হচ্ছে ‘আমি এবং আমার আইনজীবি’ বনাম ‘সে এবং তার আইনজীবি। যখন কোর্টের সামনে কেসটি আসে, এটি সাধারণত তালিকাভুক্ত করা হয় নাম দিয়ে, যেমন ‘স্মিথ বনাম স্মিথ’! তারা প্রতিপক্ষ হবে এমন পূর্বধারণা করে নেয়া হয়। দম্পতি একে অপরে প্রতি শত্রুভাবাপন্ন হবেন কি হবেন না, বা তারা বিশেষভাবে রাজী হয়েছিল কিনা যে যুক্তিসঙ্গত কারণে তারা বন্ধুভাবাপন্ন থাকবেন কি থাকবেন না। এবং কে আসলে লাভবান হবে ‘আমি জিতেছি আর তুমি হেরেছো এমন দড়ি টানাটানি হিসাবে এটিকে ভাবলে? সম্ভাবনা হচ্ছে শুধুমাত্র লাভবান হবেন দুই আইনজীবি।

হতভাগ্য দম্পতিটিকে টেনে হিঁচড়ে ‘জিরো সাম’ খেলায় জড়িয়ে ফেলা হবে, তবে আইনজীবিদের জন্য, স্মিথ বনাম স্মিথ কেসটি খুব ভালো লাভজনক একটি নন-জিরো সাম’ গেম, যেখানে স্মিথরা টাকা দেবে, এবং দুই পেশাজীবি এই দুই মক্কেলের যৌথ একাউন্ট শুষে নেবে তাদের বিস্তারিতভাবে পরিকল্পিত সাংকেতিক সহযোগিতার মাধ্যমে। একটি উপায় হচ্ছে যেখানে দুই আইনজীবি পারস্পরিক সহযোগিতা করে, সেটি হচ্ছে উভয় পক্ষ এমন কোনো প্রস্তাব উপস্থাপন করে, তারা দুজনেই জানেন যে প্রস্তাব অপর পক্ষ কখনোই মেনে নেবে না। এটি আবার একটি পাল্টা প্রস্তাবের জন্ম দেবে, এবং আবারো তারা দুজনেই জানেন কেউই তা মেনে নেবেন না। এবং এভাবেই এটি চলতে থাকে। প্রতিটি চিঠি, প্রতিটি টেলিফোন কল সহযোগিতাপূর্ণ প্রতিপক্ষের মধ্যে আদান প্রদান হয়, যা বিলের অংক আরো খানিকটা ভারী করে। ভাগ্য প্রসন্ন হলে এই প্রক্রিয়া চলতে থাকতে পারে বহু মাস অথবা এমনকি কয়েক বছর, যার সাথে সমান্তরালে বাড়তে থাকে খরচ। আইনজীবিরা একসাথে হয়ে এর কোনো মিমাংসা করেনা। বরং এর বিপরীত, সহযোগিতার জন্য সযত্নে নিজেদের এই দুরত্ব বজায় রাখাটা তাদের প্রধান অস্ত্র, যার মূল্য পরিশোধ করতে হয় তাদের মক্কেলদের। উকিলরা হয়তো নিজেরাই জানেন না তারা কি করছেন। ভ্যাম্পায়ার বাদুরদের মত– যাদের নিয়ে কিছুক্ষণের মধ্যে আমরা কথা বলবো, তারা একটি বহু চর্চিত আচারের নিয়ম অনুসরণ করছেন। এই সিস্টেমটি কাজ করে কোনো সচেতন তদারকী বা পরিকল্পনা ছাড়া। আমাদের জিরো সাম গেম খেলতে বাধ্য করার জন্য এগুলো সবই সজ্জিত। মক্কেলদের জন্য জিরো সাম, কিন্তু আইনজীবিদের জন্য খুব ভালোভাবেই নন-জিরো সাম।

 কি করা যেতে পারে? শেকসপিয়ারের প্রস্তাবটি খুব সহজ কাজ না, বহু ঝামেলার, তবে অনেক কম ঝামেলা হবে যদি আমরা আইনটি বদলাতে পারি। কিন্তু বেশীর ভাগ সংসদ সদস্যই আবার আইন পেশা থেকে এসেছেন, এবং তারা জিরো সাম মানসিকতাপুষ্ট। ব্রিটিশ হাউস অব কমনস এর চেয়ে শত্রুভাবাপন্ন জায়গা কল্পনা করা খুবই কঠিন (আইনের আদালত নিদেনপক্ষে বিতর্ক করার শ্লীলতা সংরক্ষণ করে, এবং তারা হয়তো আমার বিজ্ঞ বন্ধু এবং আমি খুব ভালোভাবে সহযোগিতা করছে ব্যাঙ্ক অবধি যাওয়ার পুরোটা পথেই।) হয়তো শুভাকাঙ্খী সংসদ সদস্যরা এবং আসলেই অনুশোচনারত আইনজীবিদের সামান্য কিছু গেম থিওরী শেখা উচিৎ। নিরপেক্ষভাবে আমাদের যোগ করা উচিৎ যে কিছু আইনজীবি এর ঠিক বিপরীত দ্বায়িত্বটি পালন করেন, তারা মক্কেলদের প্ররোচিত করেন, যারা একটি জিরো সাম গেম খেলার জন্য উন্মুখ হয়ে আছে, অথচ আদালতের বাইরে একটি নন-জিরো সাম সমঝোতা করলে তারা দুজনেই লাভবান হবে।

মানুষের জীবনে অন্য গেমগুলো তাহলে কেমন? কোনটা জিরো সাম আর কোনটা নন-জিরো সাম? এবং যেহেতু এটি একই জিনিস নয়– জীবনের কোন অংশটি আপনি অনুভব করেন জিরো অথবা নন জিরো সাম গেম? মানব জীবনের কোন অংশটি ‘ঈর্ষা বা পরশ্রীকাতরতা লালন করে এবং কোন অংশটি ব্যাঙ্কারের বিরুদ্ধে যৌথ সহযোগিতা? যেমন, ভাবুন, বেতন নিয়ে দরকষাকষি এবং ‘পার্থক্য। আমরা যখন আমাদের বেতন বৃদ্ধি নিয়ে দরকষাকষি করি, আমরা কি ঈর্ষার কারণে প্ররোচিত হই অথবা আমরা সহযোগিতা করি আমাদের সত্যিকার আয় বাড়ানো সর্বোচ্চ সুযোগের সদ্ব্যবহার করে? আমরা কি ধরে নেই, বাস্তব জীবনে এবং একই সাথে মনোবৈজ্ঞানিক গবেষণায়, যে আমরা একটি জিরো সাম গেম খেলছি, যখন আমরা সেটি করছি না? আমি শুধুমাত্র এই সব কঠিন প্রশ্নগুলো উত্থাপন করতে চাই। তবে এই প্রশ্নগুলোর উত্তর দেয়া এই বইয়ের আওতার বাইরে।

 ফুটবল হচ্ছে একটি জিরো সাম গেম। অন্তত সাধারণত এটি তাই, কখনো কখনো এটি নন-জিরো সাম গেম হতে পারে। এটি ঘটেছিল ১৯৭৭ সালে ইংলিশ ফুটবল লীগে ( অ্যাসোসিয়েশন ফুটবল বা ‘সকার’, অন্য যে খেলাগুলো পরিচিত ফুটবল হিসাবে- রাগবী ফুটবল, অস্ট্রেলিয়ান ফুটবল, আমেরিকান ফুটবল, আইরিশ ফুটবল ইত্যাদি, সব জিরো সাম গেম)। ফুটবল লীগে দলগুলোকে চারটি বিভাগে ভাগ করা হয়। একটি ক্লাৰ অন্য একটি ক্লাবের বিরুদ্ধে খেলে তাদের নিজেদের বিভাগের মধ্যে, প্রতিটি জয়ের বা ড্রয়ের জন্য পয়েন্ট সঞ্চিত করে পুরো মৌসুম জুড়ে। প্রথম ডিভিশনে থাকা সন্মানজনক এবং আরো একটি লোভনীয় এবং ব্যবসার জন্য ভালো কারণ এটি অনেক বেশী দর্শক সমাগম নিশ্চিৎ করে। প্রতিটি মৌসুমের শেষে, তালিকায় সর্বনিম্ন থাকা প্রথম ডিভিশনের তিনটি ক্লাব পরের মৌসুমে দ্বিতীয় ডিভিশনে নামিয়ে দেয়া হয়। এই পদাবনতিকে মনে করা হয় ভয়ঙ্কর একটি পরিণতি হিসাবে, যে পরিণতিকে এড়ানোর জন্য সর্ব্বোচ্চ চেষ্টা করা যুক্তিযুক্ত।

১৯৭৭ সালে ১৮মে ছিল সেই বছরের ফুটবল মৌসুমের শেষ দিন। প্রথম ডিভিশন থেকে তিনটি টিমের দুটি যারা দ্বিতীয় বিভাগে পদাবনতি পেয়েছে তারা ইতিমধ্যেই নির্দিষ্ট হয়ে গেছে, তৃতীয় কোন টীমটি তাদের নিয়তি বরণ করবে সেটি তখনও নিশ্চিৎ হয়নি। তবে সেটি সান্ডারল্যান্ড, ব্রিস্টল অথবা কভেন্ট্রি, নিশ্চিৎভাবে এই তিনটি দলের কোনো একটির হবার কথা। এই তিনটি দল, তখন, বাধ্য তাদের সব কিছু দিয়ে পরের রবিবারের খেলাটি খেলার জন্য। সান্ডারল্যান্ড খেলছিল চতুর্থ একটি টীমের সাথে ( যাদের প্রথম ডিভিশন থেকে জায়গা হারাবার ব্যাপারে কোন সন্দেহ নেই); ব্রিস্টল এবং কভেন্ট্রি ঘটনাচক্রে এক অপরের সাথে খেলছিল। আগেই জানা ছিল যে, যদি সান্দারল্যান্ড তাদের খেলায় হেরে যায়, তাহলে কভেন্ট্রি আর ব্রিস্টলের একে অপরের সাথে শুধু ড্র করতে হবে প্রথম ডিভিশনে টিকে থাকার জন্য। কিন্তু যদি সান্দারল্যান্ড জিতে যায়, তাহলে ব্রিস্টল বা কভেন্ট্রির কোনো একটি দলকে দ্বিতীয় বিভাগে নামতে হবে, যা নির্ভর করবে তাদের মধ্যকার খেলার ফলাফলের উপর। দুটি গুরুত্বপূর্ণ খেলা তাত্ত্বিকভাবে যুগপৎ ঘটছে। বাস্তব সত্য হচ্ছে যদিও ব্রিস্টল-কভেন্ট্রি ম্যাচটি পাঁচ মিনিট দেরীতে শুরু হয়েছিল। এই কারণে সান্দারল্যান্ডের খেলার খবর ব্রিস্টল-কভেন্ট্রি খেলা শেষ হবার আগেই জানা যাবে, এবং এর উপর নির্ভর করেছিল এই পুরো জটিল কাহিনীটি।

বিস্ট্রল আর কভেন্ট্রির মধ্যে প্রায় পুরোটা খেলা, সেই সময়ের একটি খবরের কাগজকে উদ্ধৃতি দিলে, দ্রুত এবং প্রায়শই হিংস্র, একটি উত্তেজনাময় ( যদি আপনি এই ধরনের খেলা পছন্দ করে থাকেন। ডিং-ডং যুদ্ধ। দুই পক্ষের কিছু দারুণ গোল খেলার আশিতম মিনিটে ফলাফল প্রায় নিশ্চিৎ করেছিল: ২-২, অর্থাৎ ড্র। তারপর খেলার শেষ দুমিনিট আগে অন্য মাঠ থেকে খবর এলো সান্দারল্যান্ড হেরে গেছে। তাৎক্ষণিকভাবে কভেন্ট্রির টীম ম্যানেজমেন্ট মাঠের এক প্রান্তে থাকা সুবিশাল ইলেকট্রনিক বোর্ডে খবরটি প্রচার করে। স্পষ্টতই ২২ জন খেলোয়াড়ই পড়তে সক্ষম এবং তারা অনুভব করেছিলেন তাদের আর এত পরিশ্রম করে খেলার কোনো প্রয়োজন নেই। দ্বিতীয় ডিভিশনে নেমে যাবার হাত থেকে বাঁচার জন্য শুধুমাত্র একটি ড্র করাই প্রয়োজন তাদের। আসলেই, এখন গোল করার জন্য কোনো বাড়তি প্রচেষ্টাই অবশ্যই খারাপ নীতি কারণ, প্রতিরক্ষা বা ডিফেন্স থেকে খেলোয়াড় সরিয়ে নেবার ঝুঁকি আছে, যা সত্যিকারভাবে হারাতে পারে –এবং দ্বিতীয় ডিভিশনে জায়গা হতে পারে। উভয় পক্ষই বিশেষভাবে আগ্রহী ছিল ড্র করার জন্য। একই খবরটি যদি উদ্ধৃত করি: ‘ সমর্থকরা যারা ব্রিস্টলের পক্ষে ডন গিলিসের ৮০ তম মিনিটে সমতাসূচক গোলটি করার আগে একে অপরের তীব্র প্রতিদ্বন্দ্বী ছিল, তারা হঠাৎ করেই যৌথভাবে উচ্ছ্বাস প্রকাশ করতে শুরু করেছিলেন। রেফারী রন শালিস অসহায়ভাবে খেলোয়াড়দের অলসভাবে বল নিয়ে এদিক ওদিক পাস দেয়া দেখতে থাকেন, যেখানে কোনো খেলোয়াড়ী প্রতিদ্বন্দ্বিতা ছিল না। যা এর আগে একটি জিরো সাম গেম ছিল সেটি হঠাৎ করে বাইরে থেকে আসা একটা টুকরো খবর পাবার সাথে সাথে একটি নন-জিরো সাম গেমে রূপান্তরিত হয়। আমাদের এর আগের আলোচনার ভাষায়, যেন একজন বাইরের ব্যাঙ্কার যাদুবলে সেখানে আবির্ভুত হলেন, যা ব্রিস্টল এবং কভেন্ট্রি উভয় টিমকেই একই পরিণতি– ড্র থেকে সুফল আদায় করার সুযোগ প্রদান করে।

 দর্শকদের খেলা যেমন ফুটবল সাধারণত খুব সঙ্গত কারণে জিরো সাম গেম। আরো বেশী উত্তেজনাময় দর্শকদের জন্য যখন তারা দেখে খেলোয়াড়রা একে অপরের সাথে তীব্রভাবে প্রতিদ্বন্দ্বিতা করছে, তারা একে পরের সাথে জোটবদ্ধ হয়ে কোনো ষড়যন্ত্র করছে এমন দৃশ্য তাদের কাম্য নয়। কিন্তু বাস্তব জীবন, মানুষের জীবন কিংবা উদ্ভিদ বা প্রাণী, এমনভাবে সাজানো নয় যে এর দর্শককে সে কোনো সুবিধা দেয়না। বাস্তব জীবনে বহু পরিস্থিতি, সত্যিকারভাবে, নন-জিরো সাম গেমের সমতুল্য। প্রকৃতি প্রায়শই ব্যাঙ্কারের ভূমিকা পালন করে এবং সেকারণে একক কোনো সদস্য অন্যের সফলতা থেকে সুবিধার আদায় করতে পারে। তারা নিজেদের সুবিধাপ্রাপ্তি নিশ্চিৎ করতে একে অপরের প্রতিদ্বন্দ্বী হবার কোনো দরকার নেই। স্বার্থপর জিনের মৌলিক সূত্র থেকে বিচ্যুত না হয়েও আমরা দেখতে পারি কিভাবে সহযোগিতা এবং পারস্পরিক সহায়তা বিকশিত হতে পারে এমনকি মৌলিকভাবে কোনো স্বার্থপর পৃথিবীতে। আমরা দেখতে পারি অ্যাক্সেলরড যেভাবে ব্যাখ্যা করেছিলেন, ভালোরাই হয়তো শেষ পর্যন্ত জয়ী হয়– বিষয়টি বুঝতে পারি।

কিন্তু এসব কিছুই হবে না যদি না খেলাটির পুনরাবৃত্তি হয়। খেলোয়াড়রা অবশ্যই জানেন (অথবা ‘জানে’) বর্তমান যে খেলাটি চলছে এটাই তাদের মধ্যে শেষ খেলা নয়। অ্যাক্সেলরডের সেই হৃদয়স্পর্শী বাক্য, ‘ভবিষ্যতের ছায়া অবশ্যই অনেক দীর্ঘ। কিন্তু এটিকে অবশ্যই কত দীর্ঘ হতে হবে? অবশ্যই এটি অসীমভাবে দীর্ঘ নয়। তাত্ত্বিক দৃষ্টিভঙ্গিতে এটি কোনো সমস্যা নয় যে খেলাটি কত দীর্ঘ; গুরুত্বপূর্ণ বিষয়টি হচ্ছে কোনো খেলোয়াড়ই আসলে জানেন না খেলাটি কখন শেষ হবে। ধরুন আমি এবং আপনি একে অপরের বিরুদ্ধে খেলছি, এবং ধরুন আমরা দুজনেই জানি এই খেলায় রাউন্ড সংখ্যা ঠিক ১০০; এখন আমরা উভয়েই বুঝতে পারি যে ১০০ তম রাউন্ডটি এই গেমের শেষ, সুতরাং কোনো সাধারণ প্রিজনার’স ডাইলেমা গেমের একটি দানের এটি সমতুল্য। সুতরাং ১০০ তম রাউন্ডে আমাদের দুজনের জন্যই একমাত্র যৌক্তিক কৌশল হচ্ছে বিশ্বাসঘাতকতা করা। এবং আমরা প্রত্যেকেই ধরে নিতে পারি অন্য খেলোয়াড়ও এটি সহজেই বুঝবেন এবং সেও শেষ রাউন্ডে বিশ্বাসঘাতকতা করার জন্য স্থিরকল্প থাকবে। সুতরাং শেষ রাউন্ড কি হবে সেটি আমরা আগে থেকেই বলে দিতে পারি পূর্বপ্রত্যাশিত উপায়ে। কিন্তু এখন ৯৯ তম রাউন্ড হবে একদানের খেলার মতই, এবং একমাত্র যৌক্তিক সিদ্ধান্ত হবে উভয় খেলোয়াড়ের জন্য এই একটি বাদে শেষ রাউন্ডে– বিশ্বাসঘাতকতা করা। এর পর ৯৮ তম রাউন্ডটি একই পরিস্থিতির স্বীকার হবে এবং এভাবে বাকী সবগুলো। দুজনই খুবই কঠোরভাবে যুক্তিবাদী খেলোয়াড়, যাদের প্রত্যেকেই ধরে নেন যে অপরজন যুক্তিবাদী, তারা বিশ্বাসঘাতকতা ছাড়া আর কিছুই করতে পারেনা যদি তারা জানতে পারেন সেই খেলাটির নিয়তিতে কয় রাউন্ড খেলা চলবে। আর এই কারণে যখন গেম তাত্ত্বিকরা পুনরাবৃত্তি হতে থাকা প্রিজনার’স ডাইলেমা গেম এর কথা বলেন, তারা সবসময় মনে করেন এই খেলার শেষটি কখন হবে সেটি আগে থেকে ভবিষ্যদ্বাণী করা সম্ভব না অথবা এটি কখন শেষ হবে সেটি জানে শুধু ব্যাঙ্কার।

এমনকি যদি খেলা কত রাউন্ড হয়েছে তার সঠিক নাম্বারটাও যদি নিশ্চিৎ জানা না থাকে, বাস্তব জীবনের প্রায়শই একটি পরিসংখ্যান নির্ভর অনুমান করা সম্ভব হয়, আর কতটা দীর্ঘ সময় ধরে খেলাটি চলতে থাকবে। এই মূল্যায়নটি পরিণত হতে পারে কৌশলের একটি গুরুত্বপূর্ণ অংশে। আমি যদি ব্যাঙ্কারকে লক্ষ করি তিনি অস্থির হয়ে বার বার তার ঘড়ির দিকে তাকাচ্ছেন, আমি তাহলে বেশ ভালোভাবে অনুমান করতে পারি যে খেলাটি প্রায় শেষ হয়ে যাচ্ছে, আমি হয়তো সেকারণে বিশ্বাসঘাতকতা করার জন্য প্ররোচিত হতে পারি। আমি যদি সন্দেহ করি আপনিও খেয়াল করেছেন যে ব্যাঙ্কার অস্থির হয়ে পড়েছেন, আমি হয়তো ভয় পাবো যে আপনিও হয়তো বিশ্বাসঘাতকতা করার কথা ভাবছেন। আমি আমার বিশ্বাসঘাতকতাটিকে আগে সম্পাদন করার জন্য সম্ভবত বেশী চিন্তিত হবো। বিশেষ করে যখন আমি হয়তো ভয় পাই যে আপনিও ভয় পাচ্ছেন যে আমিও….।

এক দানের প্রিজনার’স ডাইলেমা গেমের সাথে বহু দানে পুনরাবৃত্তি হতে থাকা প্রিজনার’স ডাইলেমা মধ্যে করা গণিতবিদদের সাধারণ বিভেদটি খুবই সরল। প্রতিটি খেলোয়াড়ের কাছে প্রত্যাশা করা যেতে পারে তারা এমনভাবে আচরণ করবে যে তার কাছে নিরন্তরভাবে হালনাগাদ হতে থাকা পরিমাপ আছে যে কত দীর্ঘ সময় ধরে খেলাটি চলতে থাকবে। যত বেশী এই পরিমান নিরুপন হবে, তত বেশী সে খেলবে গণিতবিদদের প্রত্যাশা অনুযায়ী একটি সত্যিকারের পুণরাবৃত্তি হওয়া খেলায়। অন্যভাবে, যতবেশী সে ভালো আর বেশী ক্ষমাশীল হবে, তত কম সে ঈর্ষা অনুভব করবে। খেলার ভবিষ্যৎ সম্বন্ধে তার পরিমান যত সংক্ষিপ্ত হবে, তত বেশী সে উৎসাহী হবে গণিতবিদদের প্রত্যাশা অনুযায়ী খেলার জন্য এক দানের খেলার জন্য: তত বেশী খারাপ আর কম ক্ষমাশীল সে হবে।

অ্যাক্সেলরড ভবিষ্যতের ছায়ার গুরুত্ব সম্বন্ধে একটি হৃদয়গ্রাহী উদাহরণ উপস্থাপন করেছেন, একটি উল্লেখযোগ্য প্রপঞ্চ যা গড়ে উঠেছিল প্রথম বিশ্বযুদ্ধের সময়, সেই তথাকথিত ‘বাঁচো এবং বাঁচতে দাও’ পদ্ধতি। তার উৎস ছিল ইতিহাসবিদ ও সমাজবিজ্ঞানী টনি অ্যাশওয়ার্থের গবেষণা। খুবই পরিচিত একটি বিষয় হচ্ছে যে ক্রিসমাসের সময় ব্রিটিশ এবং জার্মান সেনা সাময়িকভাবে একে অপরের সাথে সৌহার্দপূর্ণ আচরণ করেছিল এবং নো-ম্যান্স ল্যান্ডে তার একসাথে বসে পানাহারও করেছিল। অপেক্ষাকৃতভাবে যা অজানা, এবং আমার মতে আরো বেশী কৌতূহলী, সেটি হচ্ছে সেই বাস্তব তথ্যটি যে অপ্রাতিষ্ঠানিক এবং অব্যক্ত আক্রমণ বা আগ্রাসন করা হবে না এমন চুক্তি, একটি বাঁচো–এবং-বাঁচতে দাও সিস্টেম, যা বিশেষভাবে বিস্তার লাভ করেছিল ১৯১৪ খেকে শুরু থেকে পরবর্তী দুই বছর ফ্রন্টলাইন জুড়ে। একজন ঊর্ধ্বতন বৃটিশ কর্মকর্তা, ট্রেঞ্চে একবার বেড়ানোর সময় বিস্মিত হয়েছিলেন দেখেন যে তাদের নিজেদের লাইনের পিছনে রাইফেলের গুলির সীমানায় তারা বাস করছে, “আমাদের সৈন্যরা আপাতদৃষ্টিতে তাদের লক্ষ করছে না। আমি ব্যক্তিগতভাবে মনস্থির করি যে যখন আমরা দ্বায়িত্ব নেবো এই ধরনের কোনো কিছুর অনুমতি দেয়া হবেনা। এই ধরনের আচরণের অনুমতি দেয়া উচিৎ নয়। এইসব সৈন্যরা জানেই না যে একটা যুদ্ধ।

 সত্যিকারের প্রিজনার’স ডাইলেমা হিসাবে পরিগণিত হবার জন্য, কোনো সিদ্ধান্তের জন্য পুরষ্কারের পরিমান একটি ক্রমবিন্যাসের ধারাবাহিকতা অনুসরণ করে। উভয় পক্ষকে অবশ্যই পারস্পরিক সহযোগিতাকে (সহযোগিতা/সহযোগিতা) পারস্পরিক বিশ্বাসঘাতকতা থেকে শ্রেয়তর মনে করবে। বিশ্বাসঘাতকতা করা যখন অন্য পক্ষ সহযোগিতা করবে (বিশ্বাসঘাতকতা/সহযোগিতা) এমনকি আরো উত্তম যদি আপনি সেটি করে পার পেতে পারেন। সহযোগিতা করা অন্য পক্ষ যখন বিশ্বাসঘাতকতা করে (সহযোগিতা/বিশ্বাসঘাতকতা) সেটি হচ্ছে সবচেয়ে খারাপ পরিস্থিতি। পারস্পরিক বিশ্বাসঘাতকতা করা (বিশ্বাসঘাতকতা/ বিশ্বাসঘাতকতা) এটাই আর্মি কর্তৃপক্ষ চাইবেন দেখতে। তারা দেখতে চান তাদের সেনারা অতি উৎসাহী হবে জেরীদের (জার্মান) (বা টমিদের (ইংরেজ) গুলি করার জন্য। জেনারেলের দৃষ্টিভঙ্গি থেকে পারস্পরিক সহযোগিতা অনাকাঙ্খিত, কারণ এটি তাদের যুদ্ধটি জেতার জন্য কোনো সাহায্য করেনা।

সেনাপতির দৃষ্টিভঙ্গি থেকে পারস্পরিক সহযোগিতা কাঙ্খিত না, কারণ এটি তাদেরকে যুদ্ধে জয় লাভ করতে সহায়তা করবে না। কিন্তু উভয় পক্ষের একক সেনাদের দৃষ্টিভঙ্গি থেকে জন্য এটি খুবই কাঙ্খিত; তারা গুলি খেয়ে মরতে চায়না। স্বীকার করতে হবে– এবং এটি অন্যান্য লাভক্ষতির হিসাবটিও প্রভাবিত করে যা প্রয়োজন এই পরিস্তিতিটাকে একটি সত্যিকারের প্রিজনার’স ডাইলেমা হিসাবে সৃষ্টি করার জন্য– তারা সম্ভবত যুদ্ধ হারার চেয়ে বরং জেতার জন্য জেনারেলদের সাথে রাজি হবে। কিন্তু এটি কোনো বিশেষ সিদ্ধান্ত নয় যা কোনো একক সেনাকে বিশেষভাবে মুখোমুখি হতে হয়। পুরো যুদ্ধের ফলাফলের উপর খুব সম্ভবত সে এককভাবে কি করে সেটি কোনো প্রভাব ফেলে না। কোনো একটি নির্দিষ্ট শত্রু সেনারদের সাথে পারস্পরিক সহযোগিতা, যে কিনা নো-ম্যান্স ল্যান্ডের ওপারে আপনার মুখোমুখি অবস্থান করছে, অবশ্যই সুনির্দিষ্টভাবে আপনার নিয়তিকে প্রভাবিত করবে এবং পারস্পরিক বিশ্বাসঘাতকতার চেয়ে সেখানে সহযোগিতা অনেক বেশী কাম্য, এমনকি যদিও আপনি হয়তো, দেশাতৃবোধ অথবা শৃঙ্খলাজনিত কারণে হয়তো খানিকটা চাইবেন অসহযোগিতা করতে (অসহযোগিতা/সহযোগিতা) যদি আপনি সেটা করে পার পেতে পারেন। মনে হয় যেন পরিস্থিতিটি আসলে সত্যিকারের প্রিজনার’স ডাইলেমা গেম। ‘টিট ফর ট্যাটের মত কোনো কিছু এখানে গড়ে উঠবে এমন প্রত্যাশা করা যেতে পারে। এবং সেটাই হয়।

 ট্রেঞ্চের কোনো একটি নির্দিষ্ট স্থানে স্থানীয়ভাবে স্থিতিশীল কৌশলটি আবশ্যিকভাবে ‘টিট ফর ট্যাট’ নয়। টিট ফর ট্যাট হচ্ছে শুধুমাত্র ভালো, প্রতিশোধপূর্ণ কিন্তু ক্ষমাশীল কৌশলগুলোর পরিবারে একটি কৌশল মাত্র, যাদের সবগুলো, যদিও কারিগরীভাবে স্থিতিশীল, নিদেনপক্ষে খুব কঠিন অন্য কিছরু দ্বারা আগ্রাসনের স্বীকার হবার জন্য, যদি তার একবার উদ্ভূত হয়। তিনটি টিট একটি ট্যাট এর বদলে, যেমন, একটি স্থানীয় এলাকায় উদ্ভূত হয়েছিল যা সমসাময়িক একটি বিবরণ থেকে আমরা জানতে পারি।

 ‘আমরা রাতের বেলায় ট্রেঞ্চের সামনে বাইরে যাই, জার্মানদের একটি গ্রুপও তখন বাইরে, সুতরাং এসময় গুলি বিনিময়ের শিষ্ঠাচারের মধ্যে পড়ে না। সবচেয়ে বাজে জিনিস হলো রাইফেল গ্রেনেড, সেগুলো একসাথে এমনকি আট কিংবা নয়জনকে হত্যা করতে পারে যদি ট্রেঞ্চে গিয়ে পড়ে,..। কিন্তু আমরা কখনোই আমাদেরটা ব্যবহার করিনা যদি না জার্মানরা বিশেষভাবে আগ্রাসী হয়ে না ওঠে, তাদের সিস্টেম অনুযায়ী আমাদের প্রতিটি আক্রমণে তারা তিনটি প্রতি-আক্রমণ করে।

‘টিট ফর ট্যাট’ কৌশল পরিবারের যেকোনো সদস্যের জন্য এটি গুরুত্বপূর্ণ, যে খেলোয়াড়রা অসহযোগিতার জন্য শাস্তি পাবেন। বদলা নেবার ভয় অবশ্যই সবসময় সেখানে থাকে। বদলা নেবার ক্ষমতা প্রদর্শন ‘বাঁচো এবং বাচঁতে দাও’ সিস্টেমের উল্লেখযোগ্য একটি বৈশিষ্ট্য। গুলি ছুঁড়ে উভয়পক্ষই তাদের ভয়ঙ্কর দক্ষতা প্রদর্শন করতে পারে, তবে শত্রু সেনাদের প্রতি নয়, বরং শত্রু সেনাদের নিকটবর্তী কোনো প্রাণহীন নিশানার প্রতি, এই একই কৌশল ব্যবহৃত হয় ওয়েস্টার্ন সিনেমাগুলোয় ( যেমন, গুলি করে মোমবাতির শিখা নেভানো)। কেন প্রথম দুটি কার্যকর আনবিক বোমা ব্যবহার করা হয়েছিল এই বিষয়ে এখনও পর্যন্ত সন্তোষজনক কোনো ব্যাখ্যা পাওয়া যায়নি সেই সময়ে প্রথম সারির পদার্থবিদদের দৃঢ় আপত্তি সত্ত্বেও, যারা এই বোমাটি তৈরী করেছিলেন– যে বোমাগুলো ব্যবহার করা হয়েছিল দুটি শহর ধ্বংস করতে, কোনো ধরনের সতর্কতা মূলক বিস্ফোরণ ছাড়া, যা কিনা চোখ ধাঁধানো উপায়ে মোমবাতির শিখা নেভানোর মতই।

 টিট ফর ট্যাট কৌশলের একটি গুরুত্বপূর্ণ বৈশিষ্ট্য হচ্ছে তারা ক্ষমাশীল। এটি, যেমনটি আমরা আগে দেখেছি, সাহায্য করে সেই প্রক্রিয়াটিকে থামিয়ে দিয়ে, নতুবা যে প্রক্রিয়াটি পারস্পরিক বদলা নেবার একটি দীর্ঘ প্রক্রিয়া চলমান রাখে। এই বদলা নেবার প্রক্রিয়াটা থামিয়ে দেবার গুরুত্বটির নাটকীয় একটি বিবরণ আমরা পাই এক বৃটিশ সেনা অফিসারের স্মৃতিচারণে ( প্রথম দুটি বাক্যই যথেষ্ট আমাদের সন্দেহ দুর করে দেবার জন্য):

‘আমি চা পান করছিলাম ‘এ’ কোম্পানীর সাথে যখন আমরা বেশ চিৎকারের আওয়াজ শুনি এবং সেখানে আমরা অনুসন্ধানে যাই। আমরা আমাদের সেনাদের এবং জার্মান সেনাদের নিজেদের প্যারাপেটে দাঁড়িয়ে থাকতে দেখি। হঠাৎ করেই একটা বোমা এসে পড়লো কিন্তু কোন ক্ষতি করলোনা; স্বভাবতই উভয় পক্ষই মাটিতে শুয়ে পড়লো এবং আমাদের সেনারা জার্মানদের গালি দিতে শুরু করে, তখন এক সাহসী জার্মান তার আশ্রয় থেকে বের হয়ে এসে চিৎকার করে বলে, “আমরা খুব দুঃখিত বিষয়টা নিয়ে, আশা করছি আপনরা কেউ আহত হননি। এটা আমাদের দোষ না, এটা বজ্জাত প্রশিয়ান গোলন্দাজদের কাজ।

 আক্সেলরড মন্তব্য করেন এই ক্ষমাপ্রার্থনা ‘পাল্টা আক্রমণ ঠেকানোর প্রয়োজনীয় হাতিয়ার ছাড়াও আরো অনেক বেশী কিছু। এটি প্রতিফলিত করছে একটি নৈতিক অনুশোচনাবোধের, যা পারস্পরিক বিশ্বাসের একটি পরিস্থিতিতে বিঘ্নতা সৃষ্টির জন্য, এবং এটি সেই উদ্বেগটাই প্রকাশ করে যে কোনো একজন হয়তো হতাহত হয়েছে। নিশ্চয়ই প্রশংসাযোগ্য এবং খুব সাহসী জার্মান।

অ্যাক্সেলরড আরো গুরুত্ব দেন পারস্পরিক বিশ্বাসের একটি স্থিতিশীল প্যাটার্নকে রক্ষা করার বিশেষ আচার কিংবা প্রত্যাশিত আচরণের গুরুত্বের উপর। এর একটি সন্তোষজনক উদাহরণ হচ্ছে লাইনের একটি নির্দিষ্ট দিকে রাতের বন্দুক থেকে গুলি ছোঁড়ার আওয়াজ যা ব্রিটিশ গোলন্দাজ প্রতিদিন ঘড়ির কাটা মেপে নিয়মমাফিক পালন করতো। একজন জার্মান সৈন্যের ভাষায়:

 ‘প্রতিদিন সাতটায় এটি ঘটতো- এত নিয়মমাফিক যে এটি ব্যবহার করে আপনি আপনার ঘড়ির সময় ঠিক করতে পারতেন। সবসময়ই এর একটি উদ্দেশ্য থাকতো, এর নিশানা আর আওতা হচ্ছে নিখুঁত, কখনোই এদিক সেদিক এর ব্যতয় ঘটেনি বা কখনো যতদুর যাবার দরকার তার কম বেশীও হয়নি, কিছু কৌতূহলী সেনারা এমনকি হামাগুড়ি দিয়ে বাইরে আসতো সাতটার খানিকটা আগে, এই গোলাগুলো বিস্ফোরিত হতে দেখতে।

আর জার্মান গোলন্দাজরাও ঠিক একই কাজ করতো, ব্রিটিশ পক্ষে কারো বিবরণ থেকে আমরা জানতে পারি:

 ‘জার্মানরা তাদের নিশানা নির্বাচনের ব্যাপারে এত বেশী নিয়মিত যে, কর্নেল জোনস… জানতেন ঠিক কোন মিনিটে এর পরের বোমাটি এসে পড়বে ঠিক কোথায়। তার গণনা খুব বেশী নির্ভুল এবং তিনি সেই সব বড় ঝুঁকি নিতে পারতেন যা কোন অনভিজ্ঞ স্টাফ অফিসারের তুলনায়, তিনি জানতেন বোমা পড়া বন্ধ হয়ে যাবে, যে জায়গায় বোমা পড়েছে সেই জায়গা অবধি পৌঁছানোর আগেই।

অ্যাক্সেলরড মন্তব্য করেন যে এধরণের নিয়ম মাফিক এবং নিয়মিত গুলি করার আচার একটি দ্বৈত বার্তা দেয়। উপরের কমান্ডের কাছে। তারা জানান দেয় আক্রমণাত্মক আগ্রাসনের, কিন্তু শত্রুদের কাছে এটি শান্তির বার্তা বহন করে।

 ‘বাঁচো এবং বাঁচতে দাও’ সিস্টেমকে আমরা সমাধান করতে পারি মৌখিক আলোচনার মাধ্যমে, সচেতন কৌশুলীদের দ্বারা, যারা টেবিলে চারপাশে বসে দরকষাকষি করে। কিন্তু বাস্তবে সেটি ঘটেনা। স্থানীয়ভাবে পালিত কিছু নিয়মের মাধ্যমে এটি গড়ে ওঠে, পারস্পরিক ‘আচরণ’ আর ‘প্রতি-আচরণের প্রতিক্রিয়ায়। একক সৈন্যরা সম্ভবত আদৌ কখনো ভাবেননি এটি এভাবে গড়ে উঠছে। আমাদের এই বিষয়টি নিয়ে আশ্চর্য হবার কোনো প্রয়োজন নেই। অ্যাক্সেলরডে কম্পিউটারের কৌশলগুলো অবশ্যই অচেতন। এটা তাদের আচরণ যা তাকে সুনির্দিষ্ট করে সুন্দর অথবা খারাপ হিসাবে, ক্ষমাশীল বা ক্ষমা না করা, ঈর্ষান্বিত অথবা এর বিপরীত। যে সব প্রোগ্রামারটা যারা তাদের ডিজাইন করেছেন তারা এইসব কিছুর যে কোনো একটি হতে পারেন, কিন্তু সেটি অপ্রাসঙ্গিক। একটি ভালো,ক্ষমাশীল, ঈর্ষান্বিত নয় এমন কোনো স্ট্রাটেজী কোনো একটি কম্পিউটারে প্রোগ্রাম করতে পারেন খুব খারাপ একটি মানুষ। এবং ঠিক এর বিপরীতটাও ঘটতে পারে। কোনো কৌশলের ভালোত্ব চিহ্নিত করা যায় এর আচরণের দ্বারা, এর উদ্দেশ্য দিয়ে নয় (কারণ এর কোনো উদ্দেশ্য নেই) কিংবা এর লেখকের ব্যক্তিত্বের দ্বারাও না ( যখন প্রোগ্রামটি কোনো কম্পিউটারে চলতে শুরু করে তিনি প্রেক্ষাপটে হারিয়ে যান)। একটি কম্পিউটার প্রোগ্রাম একটি কৌশলগত উপায়ে আচরণ করতে পারে, সেই কৌশলটি না জেনেও অথবা আসলেই, কোন কিছু সম্বন্ধে সচেতন না হয়েই।

 আমরা অবশ্যই অবচেতন কৌশুলীদের ধারণার সাথে পুরোপুরিভাবে পরিচিত অথবা কমপক্ষে, সেই সব কৌশুলী যাদের সচেতনতা, যদি কিছু থাকে, পুরোপুরি অপ্রাসঙ্গিক। অবচেতন কৌশল অনুসরণকারীরা এই বইয়ের পাতায় প্রচুর আছে, অ্যাক্সেলরডের প্রোগ্রামগুলোই চমৎকার মডেল, যেভাবে আমরা, এই পুরো বই জুড়ে, প্রাণী এবং উদ্ভিদের কথা ভেবেছি এবং আসলেই জিনদের কথা ভেবেছি। সুতরাং খুব স্বাভাবিক জিজ্ঞাসা করা যে, তার আশাবাদী উপসংহারগুলো– ঈর্ষাকাতর নয়, ক্ষমাশীল, ভালো– এই সব কিছুই কি প্রকৃতির ক্ষেত্রে প্রযাজ্য। উত্তর হচ্ছে, হ্যাঁ, অবশ্যই তারা সেটি করে। শুধুমাত্র একটি শর্ত হচ্ছে প্রকৃতি শুধু মাঝে মাঝে প্রিজনার’স ডাইলেমা গেমের পরিস্থিতি সৃষ্টি করবে, যেন ‘ভবিষ্যতের ছায়া’ দীর্ঘতর হয় (শ্যাডো অব দ্য ফিউচার, গেম থিওরীর এই ধারণাটি বলছে, আমরা যখন কারো সাথে সময়ের পরিক্রমায় প্রায়শই ক্রিয়া-প্রতিক্রিয়া করার প্রত্যাশা করি, তখন আমরা ভিন্নভাবে আচরণ করি, এবং এভাবেই খারাপ আচরণের জন্য শাস্তি দেয়া ও পাবার প্রত্যাশা করি) এবং এই খেলা হবে নন জিরো সাম গেম ( এমন একটি পরিস্থিতি যেখানে কোনো সিদ্ধান্তকারীর লাভ অথবা ক্ষতি] আবশ্যিকভাবে অন্য সিদ্ধান্তগ্রহনকারীর ক্ষতি (বা লাভের] কারণ হবে না)। এই শর্তগুলো অবশ্যই পূর্ণ হতে হয়, প্রাণী জগতের সব জায়গায়।

কেউ কখনো দাবী করতে পারবেনা যে কোনো একটি ব্যাকটেরিয়াম হচ্ছে সচেতন স্ট্রাটেজিষ্ট, তারপরও, ব্যাকটেরিয়ীয় পরজীবিরা সম্ভবত ব্যস্ত থাকে তাদের পোষকের সাথে প্রিজনার’স ডাইলেমার অশেষ খেলায় এবং কোনো কারণই নেই কেন আমরা তাদের কৌশলের ক্ষেত্রে ‘অ্যাক্সেলরডিয়ান’ বিশেষণ ব্যবহার করতে পারবো না– ক্ষমাশীল, ঈর্ষাহীন ইত্যাদি আরো বেশ কিছু। অ্যাক্সেলরড এবং হ্যামিলটন দেখিয়েছেন যে সাধারণত ক্ষতিকর নয় বা উপকারী ব্যাকটেরিয়া খুবই ক্ষতিকর ব্যাকটেরিয়ার রূপান্তরিত হয়, এমনকি ভয়াবহ সংক্রমণ করতে পারে, আহত কোনো ব্যক্তির শরীরে। একজন ডাক্তার হয়তো বলতে পারেন যেকোনো ব্যক্তির ‘প্রাকৃতিক প্রতিবোধ’ কমে যায় কোনো আঘাতের কারণে। কিন্তু হয়তো সত্যিকারের কারণ হতে পারে প্রিজনার’স ডাইলেমার মত কোনো খেলা। ব্যাকটেরিয়াদের হয়তো কিছু লাভ করার আছে এখানে, কিন্তু তারা কেন নিজেদের দমিয়ে রাখে? মানুষ ও ব্যাকটেরিয়ার মধ্যে খেলায়, ভবিষ্যতের ছায়া সাধারণত দীর্ঘ, কারণ একটি বৈশিষ্ট্যসূচক মানুষের কাছে প্রত্যাশা করা যেতে পারে বহু বছর বাঁচবেন কোনো একটি নির্দিষ্ট সূচনা বিন্দু থেকে। কোনো খুব গুরুতর আহত মানুষ আবার অন্যদিকে হয়তো উপস্থাপন করে ভবিষ্যতের একটি অপেক্ষাকৃত একটি ক্ষুদ্রতর ছায়া তাদের ব্যাকটেরিয় অতিথিদের। বিশ্বাসঘাতকতা করার প্ররোচনা’ একইসাথে দেখতে আরো বেশী আকর্ষণীয় পছন্দ মনে হয় ‘পারস্পরিক সহযোগিতার পুরষ্কারের চেয়ে। বলার প্রয়োজনের অপেক্ষা রাখে না যে, এমন কোনো প্রস্তাব নেই যে ব্যাকটেরিয়া এসব হিসাবনিকাশ বের করছে তাদের খারাপ ছোট মাথায়! বহু প্রজন্মের ব্যাকটেরিয়ার উপর নির্বাচন সম্ভবত একটি অবচেতন গড়পড়তা নিয়ম বা ‘রুল অব থাম্ব বের করেছেন, যা বিশুদ্ধভাবে জৈবরাসায়নিক উপায়ে কাজ করে।

 অ্যাক্সেলরড ও হ্যামিলটনের মতে, এমনকি উদ্ভিদরাও প্রতিশোধ নিতে পারে, আবারও অবশ্যই সচেতনভাবে নয়। ডুমুর গাছ ও ফিগ ওয়াস্পদের একটি অন্তরঙ্গ সহযোগিতামূলক সম্পর্ক বিদ্যমান। যে ডুমুরটি আপনি খান, সেটি আসলে ফল নয়, এর মাথায় একটি ছোট ছিদ্র আছে, আপনি যদি সেই ছিদ্র দিয়ে ভিতরে প্রবেশ করতে পারেন (আপনাকে সেই কাজ করার জন্য ফিগ ওয়াস্পদের মত ছোট হতে হবে, এবং ছিদ্রটি খুবই ছোট, সৌভাগ্যক্রমে আপনি যখন ডুমুর খান সেটি নজরে না পড়ার মতই ছোট), আপনি এর ভিতরের দেয়াল জুড়ে শত শত ছোট ছোট ফুল দেখতে পাবেন। ডুমুর আসলেই অনেকটা ফুলদের জন্য একটি অন্ধকার, গরম হটহাউজের মত, একটি আভ্যন্তরীণ পরাগায়ন কক্ষ। এবং যে একমাত্র উপায়টি তাদের পরাগায়ন করাতে পারে তা হলো ছোট ফিগ ওয়াস্প। তাহলে গাছ সুবিধা পায় এই ওয়াস্পগুলোকে জায়গা দেবার জন্য। কিন্তু ওয়াস্পদের এখানে কি লাভ আছে। এই সব ছোট ফুলগুলোর কোনো কোনোটায় তারা ডিম পাড়ে, ডিম ফুটে বের হওয়া লার্ভা যে ফুলগুলো পরে খাদ্য হিসাবে গ্রহন করে। তারা একই ডুমুরের অন্য ফুলদের পরাগায়ন করে। এই সব লার্ভাদের জন্য বিশ্বাসঘাতকতা মানে অনেক বেশী সংখ্যক ফুলে ডিম পাড়া এবং কম ফুলকে পরাগায়ন করা। কিন্তু ডুমুর গাছ কিভাবে বদলা নিতে পারে? অ্যাক্সেলরড ও হ্যামিলটনের জানান, দেখা গেছে বেশীর ভাগ ক্ষেত্রেই যদি কোনো ফিগ ওয়াস্প একটি তরুণ ডুমুরে প্রবেশ করে যথেষ্ট পরিমান ফুলকে বীজের জন্য পরাগায়ন না করে বরং তার পরিবর্তে ডিম পাড়ে প্রায় অধিকাংশ ফুলের মধ্যে, তখন ডুমুর গাছ সেই ডুমুরটির বৃদ্ধি স্থগিত করে দেয় বেশ আগের একটি স্তরে। সেই ওয়াস্প এর সব উত্তরসূরীরা মারা যায়।

আরেকটি অদ্ভুত উদাহরণ যা প্রকৃতিতে এই টিট ফর ট্যাট বন্দোবস্তের মত, একটি উভলিঙ্গ মাছের মধ্যে সেটি আবিষ্কার করেছিলেন এরিক ফিশার– সি ব্যাস। আমাদের ব্যতিক্রম, তাদের ভ্রূণাবস্থায় ক্রোমোজোমের মাধ্যমে এই মাছগুলোর লিঙ্গ নির্ধারিত হয় না। বরং প্রতিটি মাছই স্ত্রী এবং পুরুষ দুটি ভূমিকাই পালন করতে সক্ষম। সন্তান জন্ম দেবার কোনো একটি পর্বে তারা হয় ডিম পাড়ে অথবা শুক্রাণু নিঃসরণ করে। তারা সাধারণত একগামী সম্পর্কের জোড় বাধে, এবং পালাক্রমে পুরুষ ও স্ত্রী সদস্যের ভূমিকা নেয়। এখন, আমরা একটি ধারণা করতে পারি যে কোনো একটি একক সি ব্যাস মাছ, যদি পার পেতে পারে, প্রতিবারই এটি পুরুষের ভূমিকা পালন করতে পছন্দ করবে, কারণ এখানে পুরুষের ভূমিকাটা অপেক্ষাকৃতভাবে সহজ বা শক্তি ব্যবহারের হিসাবে অপেক্ষাকৃতভাবে কম ব্যয়সাধ্য। অন্যভাবে বিষয়টি বললে, কোনো একটি মাছ যে কিনা তার সঙ্গীকে রাজী করাতে পারবে বেশীর ভাগ সময় নারীর ভূমিকা নেবার জন্য, সে ডিমের জন্য ‘তার (স্ত্রী) করা সব অর্থনৈতিক বিনিয়োগের সুফল পাবে, একই সাথে তার (পুরুষ) উদ্বৃত্ত সম্পদ থাকবে অন্যান্য নানা জিনিসে সেটি বিনিয়োগ করার জন্য, যেমন অন্যান্য মাছের সাথে প্রজনন।

বাস্তবিকভাবে ফিশার যা পর্যবেক্ষণ করেছেন তা হলো মাছগুলো একটি কঠোর নিয়মমাফিক পালাক্রমে এই দায়িত্ব পালনের পদ্ধতিটি অনুসরণ করে। এটাই ঠিক আমাদের আশা করা উচিৎ যদি তারা ‘টিট ফর ট্যাট’ গেম খেলে থাকে। এবং এটিও সম্ভব যে তাদের সেটি করা উচিৎ, কারণ দৃশ্যতই মনে হয় এটি একটি সত্যিকারের প্রিজনার’স ডাইলেমা গেম, যদিও খানিকটা জটিল প্রকৃতির। ‘সহযোগিতার কার্ড খেলা মানে স্ত্রী খেলোয়াড়দের ভূমিকা পালন করা যখন আপনার সেটি করার পালা। কোনো পুরুষের ভূমিকা পালন করার চেষ্টা করা যখন তার পালা স্ত্রীর ভূমিকা পালন করার, সেটি অসহযোগিতা বা বিশ্বাসঘাতক খেলার সমতুল্য। বিশ্বাসঘাতকতার সম্ভাবনা থাকে বদলার শিকার হবার, সঙ্গী এর পরের বার স্ত্রীর ভূমিকা পালন নাও করতে পারে, যখন সেটি তার করার পালা। অথবা সে (স্ত্রী) পুরো সম্পর্কটি শেষ করে দিতে পারে। ফিশার সত্যি এটি পর্যবেক্ষণ করেছিলেন যে মাছের জুটিতে লিঙ্গ দ্বায়িত্ব পালনে অসাম্যতা জুটি ভাঙ্গার প্রবণতা সৃষ্টি করে।

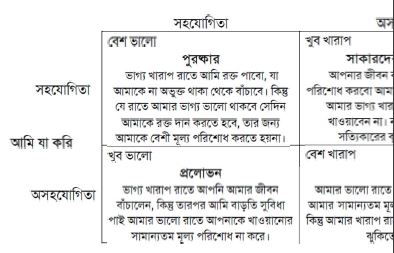
একটি প্রশ্ন সমাজবিজ্ঞানী এবং মনোবিজ্ঞানীরা মাঝে মাঝে জিজ্ঞাসা করেন কেন রক্তদাতারা (কিছু দেশে যেমন ব্রিটেন, যেখানে এর জন্য কোনো মূল্য পরিশোধ করা হয়না) রক্ত দান করেন। আমার মনে হয় যেকোনো অর্থে এখানে খুব কঠিন হবে বিশ্বাস করা যে উত্তরটি আছে সাধারণ বোধগম্য অর্থে ছদ্ম স্বার্থপরতা অথবা পারস্পরিক পরার্থবাদিতায় কিছু পাবার আশায়। এমন নয় যে নিয়মিত রক্ত দাতারা বিশেষ সুবিধা পান যখন তাদের রক্ত সঞ্চালনের প্রয়োজন। হয়। এমন নয় যে পরে থাকার জন্য তাদের ছোট সোনালী কোনো স্টার দেয়া হয়। হয়তো আমি খানিকটা অবুঝ, কিন্তু আমি এটিকে সত্যিকারের বিশুদ্ধ, নিঃস্বার্থ পরার্থবাদের একটি উদাহরণ হিসাবে দেখার জন্য প্ররোচিত হবার তাড়না অনুভব করছি। তবে সেটি যাই হোক না কেন, ভ্যাম্পায়ার বাদুড়দের মধ্যে রক্ত ভাগাভাগি মনে হয় অ্যাক্সেলরডের মডেলের সাথে সঙ্গতিপূর্ণ হয় বেশ ভালোভাবে। আমরা এটা জানতে পারি জি, এস. উইলকিনসনের গবেষণা থেকে।

ভ্যাম্পায়ার বাদুড়রা, যেমন ভ্যাম্পায়াররা সুপরিচিত, রাতের বেলায় রক্ত পান করে। এবং খাওয়া পাওয়া তাদের জন্য খুব একটা সহজ কাজ নয়, কিন্তু যদি তারা পায় সেটি সাধারণত বেশ বড় কোনো শিকার হয়। যখন ভোর হয়, বাদুড়ের পালে কিছু সদস্যের ভাগ্য তেমন ভালো থাকেনা, তারা ফিরে আসে পুরোপুরি খালি পেটে, কিন্তু সেই সব বাদুড়রা রাতে যারা শিকার খুঁজে পেয়েছিল তাদের সম্ভাবনা থাকে প্রয়োজনের চেয়ে বেশী পরিমান রক্ত চোষার। পরবর্তী কোনো রাতে ভাগ্যের চাকা অন্যদিকে ঘুরতে পারে। সুতরাং পারস্পরিক সহযোগিতার মত প্রতিশ্রুতিশীল বিষয়টি এখানে কাজ করে বলে মনে করা হয়। উইলকিনসন দেখেছিলেন, যে সদস্যরা বেশী ভাগ্যবান কোন একটি রাতে তারা আসলেই মাঝে মাঝে রক্ত দান করে তাদের অভুক্ত সদস্যদের, কাজটি করে তারা তাদের পাকস্থলী থেকে রক্ত উগরে দেবার মাধ্যমে, যেন তাদের অপেক্ষাকৃত কম ভাগ্যবান কোন সদস্য সেটি পান করতে পারে। উলকিনসন যে সংখ্যক এভাবে রক্ত উগরিয়ে দেবার ঘটনা দেখেছেন তাদের ৭৭ টি খুব সহজেই বোঝা সম্ভব মা বাদুড়দের তাদের সন্তানদের খাওয়ানোর ঘটনা হিসাবে, কিন্তু আরো অনেক উদাহরণের ক্ষেত্রে আমরা দেখি এই রক্ত ভাগ করার সাথে জড়িত তাদের জিনগত আত্মীয় এমন সদস্যরা। কিন্তু তারপরও কিছু রক্ত ভাগাভাগি করার উদাহরণ আমরা দেখি, সেটি ঘটে আত্মীয় নয় এমন বাদুড় সদস্যদের মধ্যে। এই সব ঘটনাগুলোয় ‘রক্ত পানির চেয়ে ভারী’ ব্যাখ্যা বাস্তব সত্যের সাথে সামঞ্জস্যপূর্ণ নয়। গুরুত্বপূর্ণভাবে এখানে যে সদস্যদের মধ্যে আমরা রক্ত ভাগাভাগি হতে দেখি তাদের প্রায়শই একই জায়গায় ঘুমায় বা বিশ্রাম নেয় বা রুষ্টমেট। তাদের একে অপরের সাথে ক্রিয়া-প্রতিক্রিয়া করার সম্ভাবনা আছে বারবার, যেমনটি দরকার পুনরাবৃত্তি হওয়া প্রিজনার’স ডাইলেমা গেমের মত কোনো পরিস্থিতি হবার মত। কিন্তু প্রিজনার্স ডাইলেমার অন্য শর্তগুলো কি পূরণ হয়? নীচের মূল্য পরিশোধের ছকটি (ছবি ৪) দেখতে হবে সেকরম যদি তারা প্রিজনার’স ডাইলেমা গেমটি খেলে আমরা যেমনটি প্রত্যাশা করছি।

 বিশেষ করে, এই সব বাদুড়গুলো কি একে অপরকে আলাদা বাদুড় হিসাবে চিনতে পারে? উইলকিনসন একটি পরীক্ষা করেছিলেন বন্দী বাদুড়দের নিয়ে, প্রমাণ করেছিলেন তারা সেটি করতে পারে। মূল ধারণাটি ছিল এক রাতের জন্য একটি বাদুড়কে সরিয়ে ফেলা হয়, তাকে না খাইয়ে রাখা হয় যখন বাকী সবাই খাবে। এই দুর্ভাগা ক্ষুধার্ত বাদুড়টিকে এরপর তার বিশ্রাম করার স্থানে রেখে আসা হয়। এবং উইলকিনসন লক্ষ রাখেন, কে, যদি কেউ, একে খাদ্য দান করে। এই পরীক্ষাটি যদি বহুবার পুনরাবৃত্তি করা হয়, প্রতিটি বাদুড় পালাক্রমে অভুক্ত শিকার হিসাবে তাদের দ্বায়িত্ব পালন করে। মূল বিষয়টি হচ্ছে এই বন্দী বাদুড়দের জনগোষ্ঠী দুটি পৃথক গ্রুপের মিশ্রণ। যাদেরকে এমন গুহা থেকে সংগ্রহ করা হয়েছে যার মধ্যে দুরত্ব বহু মাইলের। যদি ভ্যাম্পায়াররা সক্ষম হয় তাদের বন্ধুদের শনাক্ত করতে, তাহলে পরীক্ষামূলকভাবে অভুক্ত রাখা বাদুড়গুলোকে দেখতে পাওয়া উচিৎ শুধুমাত্র খাওয়া পাচ্ছে তাদের মূল গুহায় বাসকারী সদস্যদের দ্বারা।

মোটামুটি যা ঘটে তাহচ্ছে, মোট তেরটি দান করার ঘটনা পর্যবেক্ষণ করা হয়, এবং তেরোটির মধ্যে বারোটি, দাতা বাদুড়টি ছিল অভুক্ত বাদুড়টির পুরোনো বন্ধু, যাদের একই গুহা থেকে সংগ্রহ করা হয়েছে। তেরটি দৃষ্টান্তের শুধুমাত্র একটিতে আমরা দেখি অভুক্ত বাদুড়কে খাওয়াচ্ছে নতুন বন্ধু, এবং তাদের একই গুহা থেকে সংগ্রহ করা হয়নি। অবশ্যই বিষয়টি কাকতালীয় কোনো ব্যপার হতে হবে, কিন্তু আমরা এমন কিছু ঘটার বিরুদ্ধে সম্ভাবনাটা পরিমাপ করতে পারি। সেই সম্ভাবনার পরিমান প্রতি ৫০০ বারে একবার। সুতরাং যথেষ্ট নিরাপদ এমন কোনো উপসংহারে পৌঁছানো বাদুড়রা আসলেই পক্ষপাতদুষ্ট তাদের পুরোনো বন্ধুদের খাওয়ানোর ব্যপারে, যখন তারা অন্য গুহা থেকে আসা অপরিচিত আর প্রাকপরিচিত বাদুড়ের মধ্যে কাকে খাদ্য দান করবে এমন কোনো পরিস্থিতির মুখোমুখি হয়।

ভ্যাম্পায়াররা দারুণ দক্ষ নানা কল্পকাহিনীর জন্ম দেবার জন্য। ভিক্টোরীয় গথিক ভাবনার অনুসারীদের কাছে তারা হচ্ছে সেই অন্ধকারের শক্তি যারা রাতকে সন্ত্রস্ত করে রাখে, জীবনের প্রাণশক্তিকে শুষে খায়, নিরপরাধ মানুষকে বিসর্জন দেয় শুধুমাত্র তার তৃষ্ণা নিবারণ করার জন্য। এটাকে যুক্ত করুন ভিক্টোরীয় যুগের আরেকটি কল্পকাহিনীর সাথে, দাতে ও নখরে সজ্জিত হিংস্র প্রকৃতি এবং ভ্যাম্পায়াররা স্বার্থপর জিনের এই পৃথিবীর সম্বন্ধে আমাদের গভীরতম ভয়েরই পুনরুজ্জীবিত রুপ নয় কি? আমার ক্ষেত্রে, আমি সব পুরাণ কাহিনীর ব্যাপারেই সন্দিহান। যদি আমরা তাদের জানাতে চাই সত্য কোথায় অবস্থান করছে সুনির্দিষ্ট উদাহরণগুলোতে, আমাদের বিষয়টি খতিয়ে দেখতে হবে। ডারউইনীয় ব্যাখ্যার বিশাল ভাণ্ডার আমাদের যা দিচ্ছে সেটি কোনো একটি নির্দিষ্ট জীব সম্বন্ধে আমাদের বিস্তারিত প্রত্যাশা নয়। এটি আমাদের আরো সূক্ষ্মতর কিছু প্রদান করে এবং আরো মূল্যবান– একটি মূলনীতিকে বোঝার ক্ষমতা। কিন্তু যদি পুরাণ কাহিনীকে এক্ষেত্রে আমাদের অনুভব করতেই হয়, ভ্যাম্পায়ারদের সম্বন্ধে সত্যিকার তথ্য একটি ভিন্ন নীতিকথা আমাদের শেখাতে পারে। বাদুড়দের নিজেদের ক্ষেত্রে, শুধুমাত্র রক্তই পানির চেয়ে ভারী নয়, তারা আত্মীয়তার বন্ধনকে অতিক্রম করতে পারে, তাদের নিজস্ব অনুগত রক্ত-নির্ভর ভাতৃত্বের গোত্র গড়ে তুলতে পারে। একটি স্বস্তিকর নতুন পুরাণের ভ্যানগার্ড হতে পারে ভ্যাম্পায়াররা, ভাগাভাগি করে নেবার পুরাণ, পারস্পরিক সহযোগিতার একটি সম্পর্ক, তারাই সূচনা করতে পারে প্রসন্ন আর কল্যাণময় সেই ধারণাটি, এমনকি যখন স্বার্থপর জিনের হাতে রাশ ধরা থাকে, ভালোরা সফল হতে পারে।